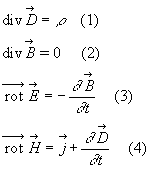
Equation de conservation du flux de
Equation de Maxwell-Faraday (phénomène d'induction)
Equation de Maxwell-Ampère
Les ondes électromagnétiques
Plan
1. Rappel sur les équations de Maxwell
2. Equations de propagation en Electromagnétisme
3. L'onde électromagnétique dans le vide
4. L'onde électromagnétique dans un diélectrique
5. L'onde électromagnétique dans un conducteur
6. Energie des ondes électromagnétiques
7. Equations de Maxwell et approximation des états
quasi-stationnaires
8. Les différents types d'ondes électromagnétiques
1. Rappel sur les équations
de Maxwell
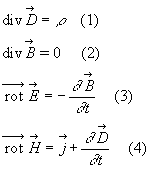 |
Equation de Maxwell-Gauss : Equation de conservation du flux de Equation de Maxwell-Faraday (phénomène d'induction) Equation de Maxwell-Ampère |
![]() est le champ
électrique, le d
est le champ
électrique, le d![]() éplacement
(ou induction) électrique,
éplacement
(ou induction) électrique, ![]() le champ (ou induction) magnétique,
le champ (ou induction) magnétique, ![]() l'excitation (ou champ) magnétique,
l'excitation (ou champ) magnétique, ![]() la
densité volumique de charges réelles,
la
densité volumique de charges réelles, ![]() la densité volumique de courants de charges réels.
la densité volumique de courants de charges réels.
![]() [
[![]() pour un milieu
linéaire, homogène et isotrope]
pour un milieu
linéaire, homogène et isotrope]
![]() est le vecteur
polarisation,
est le vecteur
polarisation, ![]() la susceptibilité diélectrique et
la susceptibilité diélectrique et ![]() la permittivité du diélectrique.
la permittivité du diélectrique.
![]() [
[![]() pour un milieu
linéaire, homogène et isotrope]
pour un milieu
linéaire, homogène et isotrope]
![]() est le vecteur
aimantation,
est le vecteur
aimantation, ![]() la susceptibilité magnétique et
la susceptibilité magnétique et ![]() la perméabilité du milieu magnétique.
la perméabilité du milieu magnétique.
Conditions de passage à la surface de séparation de
deux milieux
Les milieux sont notés 1 et 2, le vecteur unitaire normal ![]() est orienté du milieu 1 vers le milieu 2.
est orienté du milieu 1 vers le milieu 2.
L'application des équations de Maxwell donne à la frontière
des deux milieux :
![]() équations
auxquelles il convient d'ajouter la continuité du potentiel qui se déduit
de la continuité de la composante tangentielle du champ électrique.
équations
auxquelles il convient d'ajouter la continuité du potentiel qui se déduit
de la continuité de la composante tangentielle du champ électrique.
2. Equations de propagation en Electromagnétisme
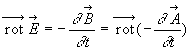 ð
Il existe une fonction scalaire V appelé potentiel scalaire
telle que
ð
Il existe une fonction scalaire V appelé potentiel scalaire
telle que 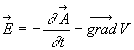 où V n'est pas défini de manière unique puisque
un gradient n'est défini qu'à une constante additive près
et puisque le potentiel vecteur n'est défini qu'au gradient d'une fonction
quelconque près.
où V n'est pas défini de manière unique puisque
un gradient n'est défini qu'à une constante additive près
et puisque le potentiel vecteur n'est défini qu'au gradient d'une fonction
quelconque près.2.1. Equation de propagation de ![]()

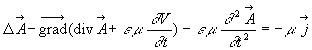
Nous avons vu qu'il existait plusieurs couples de valeurs possibles (![]() )
et nous choisissons celui qui vérifie
)
et nous choisissons celui qui vérifie
![]()
Ce résultat important est connu sous le nom de relation de jauge de
Lorentz.
Ainsi, nous obtenons l’équation de propagation 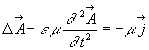
Jauge de Lorentz
Soit le couple (![]() )
vérifiant
)
vérifiant ![]() et
et 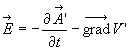 .
.
Nous formons un autre potentiel vecteur par la relation ![]() .
En reportant dans l’expression de
.
En reportant dans l’expression de ![]() ,
,
on trouve ![]() .
.
La question est de savoir s’il est possible de trouver une fonction f
telle que le couple (![]() )
vérifie la jauge de Lorentz ?
)
vérifie la jauge de Lorentz ?
En remplaçant dans cette relation, on obtient l’équation aux dérivées
partielles ![]() qui
permet de calculer la fonction f ou, surtout, qui prouve que cette fonction
existe.
qui
permet de calculer la fonction f ou, surtout, qui prouve que cette fonction
existe.
2.2. Equation de propagation de V
![]()
![]()
2.3. Equation de propagation de ![]()

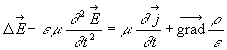
2.4. Equation de propagation de ![]()
![]()
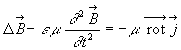
3. L'onde électromagnétique dans le vide
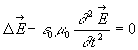 ;
; 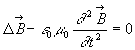
Nous avons étudié jusqu'à présent des équations
aux dérivées partielles d’une grandeur scalaire à
une dimension d'espace ; ici nous devons traiter des équations aux
dérivées partielles pour des grandeurs vectorielles (trois
dimensions d'espace).
Le champ électrique et le champ magnétique sont reliés
dans les équations de Maxwell (il s’agit d’un champ électromagnétique),
ils ont été découplés en utilisant des dérivations
pour former les équations de propagation.
Nous avons déjà noté que les techniques des séries
de Fourier ou de la transformée de Fourier permettent de se ramener à
une étude de base où la dépendance avec le temps est de
la forme ![]() .
.
Nous posons ![]() et
et ![]() .
.
On appelle onde plane monochromatique le cas particulier où ![]() ne
sont fonctions que d'une seule variable cartésienne soit, par exemple,
x.
ne
sont fonctions que d'une seule variable cartésienne soit, par exemple,
x.
![]() ð
ð![]() le champ électrique de l'onde n'a pas de composante suivant x.
le champ électrique de l'onde n'a pas de composante suivant x.
![]() ð
ð![]() le champ magnétique de l'onde n'a pas de composante suivant x.
le champ magnétique de l'onde n'a pas de composante suivant x.
Le champ électromagnétique est contenu dans des plans
perpendiculaires à l'axe des x.
Un choix judicieux de l'axe des y permet d'écrire ![]() .
.
En reportant dans l'équation de propagation, on obtient ![]() (
(![]() )
)
et ![]()
Nous trouvons, pour le cas particulier de l'onde plane monochromatique,
la superposition de deux ondes (progressive et régressive) se propageant
à vitesse c, appelée " vitesse de la lumière
".
Nous continuons l'étude avec l'onde progressive et calculons le champ
magnétique à partir de la relation 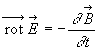 qui
entraîne
qui
entraîne ![]()
Pour l'onde progressive, le vecteur vitesse est égale à ![]() et
et ![]()
Cette dernière relation reste vérifiée pour l'onde régressive
à condition d'écrire ![]()
Remarque : on notera bien que ces relations ne sont vraies que pour
les ondes planes monochromatiques. Il en est de même pour le vecteur d'onde ![]() qui,
d'une manière générale pour une propagation suivant la
direction x, s'écrit
qui,
d'une manière générale pour une propagation suivant la
direction x, s'écrit ![]() avec
avec ![]() .
.
4. L'onde électromagnétique dans un diélectrique
Ce qui est dit dans le paragraphe précédent reste vrai en remplaçant ![]() par
par ![]() . La vitesse
de propagation de l'onde devient
. La vitesse
de propagation de l'onde devient ![]() où n est l'indice de réfraction (voir cours d'optique géométrique)
du milieu (
où n est l'indice de réfraction (voir cours d'optique géométrique)
du milieu (![]() ).
).
On notera que les milieux diélectriques sont, à priori, dispersifs
puisque ![]() [la
polarisation dépend de la fréquence du champ excitateur - voir
théorie de l'électron
élastiquement lié]
[la
polarisation dépend de la fréquence du champ excitateur - voir
théorie de l'électron
élastiquement lié]
5. L'onde électromagnétique dans un conducteur
Nous supposons vérifiées les conditions de validité de
la loi d'Ohm ![]() (nous excluons le domaine des hyperfréquences), ce qui entraîne
que la densité volumique de charges
(nous excluons le domaine des hyperfréquences), ce qui entraîne
que la densité volumique de charges ![]() est nulle.
est nulle.
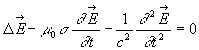 ;
; 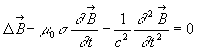
La direction x est choisie comme direction d'écoulement du courant et nous considérons un conducteur en forme de plaque de dimensions supposées infinies dans la direction des z plutôt qu'un conducteur à symétrie de révolution pour lequel la résolution amène à utiliser des fonctions de Bessel.
![]() ð
ð![]()
Pour résoudre cette équation aux dérivées partielles,
nous utilisons la technique de séparation de variables en posant ![]() .
.
On obtient ![]()
En se limitant à une onde progressive et un conducteur suffisamment
épais (direction y importante) ![]()
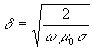 ).
).Il est commode de définir le vecteur de Poynting ![]() .
.
L'analyse vectorielle conjuguée aux équations de Maxwell
donne :
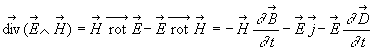
Nous reconnaissons :
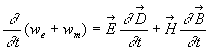 où
où En reprenant la démonstration des équations de propagation, on
remarque que les phénomènes de propagation sont liés à
l'existence du terme ![]() (
(![]() ).
).
Dans le cadre de l'approximation des états quasi-stationnaires,
les équations de Maxwell s'écrivent :
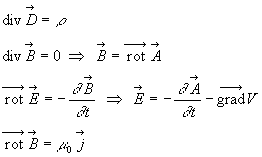
Par suite, la conservation de la charge devient ![]() : dans l'approximation des états quasi-stationnaires,
: dans l'approximation des états quasi-stationnaires, ![]() (la
densité volumique de charges est constante ou nulle).
(la
densité volumique de charges est constante ou nulle).
La relation de jauge de Lorentz devient celle de Coulomb (![]() ).
).
8. Les différents types d'ondes électromagnétiques
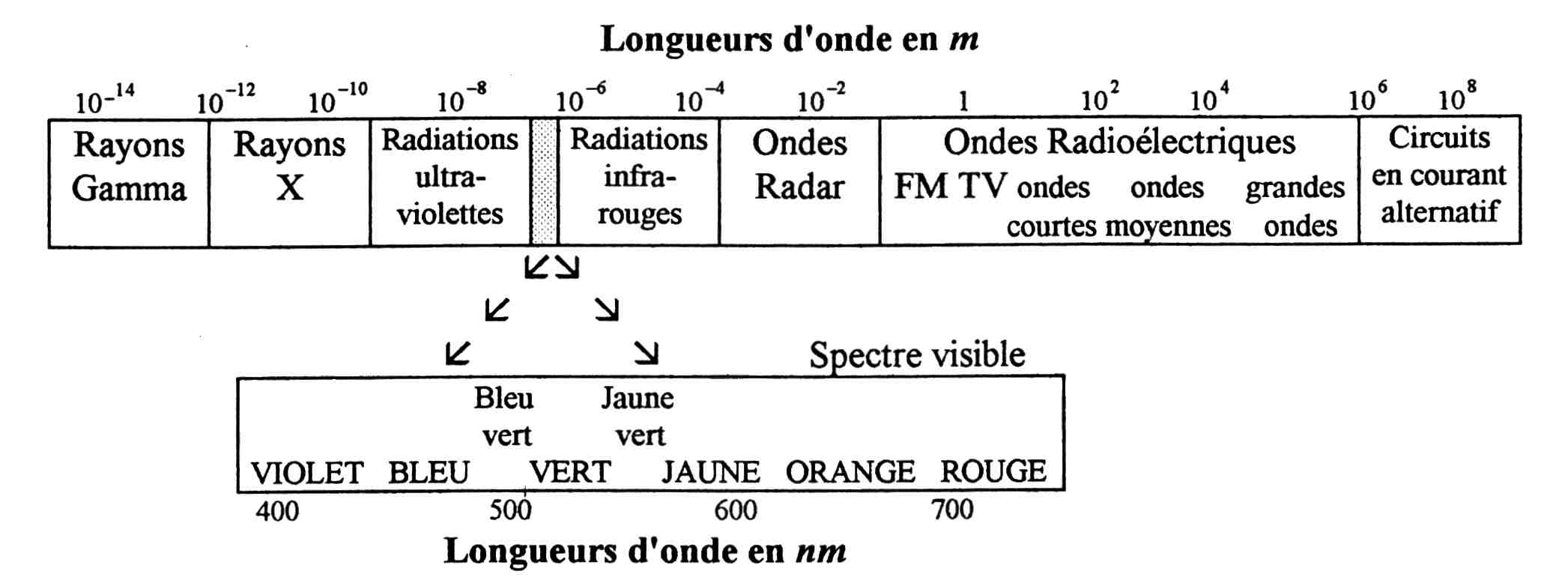
Le domaine des longueurs d'onde inférieures à ![]() est communément appelée Optique : il étudie tout
ce qui concerne la lumière et nécessite d'être présenté
en tant que tel.
est communément appelée Optique : il étudie tout
ce qui concerne la lumière et nécessite d'être présenté
en tant que tel.
Le domaine des longueurs d'onde supérieures au centimètre
est celui des ondes radio, le phénomène de propagation devenant
négligeable si la longueur d'onde est grande (circuits électriques).
Les deux problèmes intitulés " Ondes électromagnétiques non planes " et " Théorie des antennes " sont, à notre avis, indispensables pour une bonne compréhension des phénomènes de propagation des ondes électromagnétiques.
A travers les chapitres " La matière en présence d'un
champ électrique ", " La matière en présence d'un
champ magnétique " et " Les ondes électromagnétiques
", tous les fondements nécessaires à l'étude des circuits
électriques en régime continu, en régime transitoire
ou en régime forcé sont établis.
Outre les notions de résistances, condensateurs, selfs, coefficients
d’influence mutuelle, des approfondissements sur :
- les générateurs,
- les récepteurs,
- les diodes,
- les transistors,
- l'amplificateur opérationnel,
- les lois de Kirchoff (loi des noeuds, loi des mailles),
- les théorèmes de Thévenin, Norton et Millman,
- la transformation triangle-étoile,
s’avèrent indispensables pour aborder ces domaines de la
Physique appliquée