Suite à une excitation en
Exemples d'ondes mécaniques
| Plan
1. L'onde sonore
|
Les
illustrations et animations de Yves Cortial
Corde de Melde : modèle simple
et amélioré
|
Pour les ondes mécaniques, la quantité se propageant est
une grandeur scalaire liée à la matière.
Nous limitons nos propos à :
- l'onde sonore qui est une onde de pression.
Localement la pression est liée à la densité locale
de molécules, une variation locale de pression implique une variation
de la densité qui se propage par les chocs entre molécules.
- la corde vibrante qui est un exemple d'onde de déformation
de matière.
La première étude sera un exemple d'onde longitudinale, la seconde d'onde transversale.
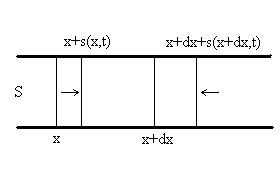
Nous limitons l'étude au cas d'une onde unidimensionnelle se
propageant dans un fluide non visqueux de section constante.
 |
Nous considérons une tranche de fluide au
repos entre les sections Suite à une excitation en |
La résultante de ces forces est non nulle, la tranche ![]() se déplace à vitesse
se déplace à vitesse ![]() et sera au temps t en
et sera au temps t en ![]() si
si ![]() représente
le déplacement de cette tranche.
représente
le déplacement de cette tranche.
![]() représente
la vitesse de la matière, elle n’est pas à confondre avec la vitesse
de phase de l’onde.
représente
la vitesse de la matière, elle n’est pas à confondre avec la vitesse
de phase de l’onde.
![]() représente
le débit volumique.
représente
le débit volumique.
Au temps ![]() ,
elle sera située en
,
elle sera située en ![]() .
.
Pendant un temps dt, la tranche x se sera déplacé
de ![]() ð
ð![]()
Remarque : les déplacements de matière se produisent
dans la même direction x que la propagation de l'onde, l'onde
sonore est donc longitudinale.
L'onde sonore n'est pas le seul exemple d'onde longitudinale. Il en
existe dans les solides de dimensions finies (vibration dans les barres)
ou de dimensions infinies (tremblement de terre par cisaillement).
Accroissement relatif de volume
La tranche ![]() se déplace, elle est située en
se déplace, elle est située en ![]() au temps t.
au temps t.
La tranche dx ne garde pas une largeur constante et on calcule
l'accroissement relatif de volume de la tranche d’épaisseur dx
située en x.
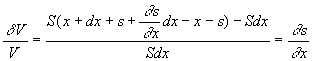
Cette quantité peut être reliée aux propriétés
thermodynamiques de la matière en introduisant le coefficient de compressibilité
adiabatique ![]()
On obtient![]()
Remarques :
Calculons l'accélération d'une particule située au temps
t en x de vitesse ![]() .
Cette particule au temps
.
Cette particule au temps ![]() sera
en
sera
en ![]() telle
que
telle
que ![]() .
.
La variation de vitesse ![]() entre les instants
entre les instants ![]() est
égale à
est
égale à ![]() et l'accélération
et l'accélération ![]()
Ce type de dérivée très utilisé en Mécanique
des milieux continus est connu sous le nom de dérivée particulaire
( notation ![]() ).
).
En fait, l’étude générale de l’onde sonore
entre dans le cadre plus large de la Mécanique des fluides.
L'application du Théorème de la résultante dynamique
conduit à :
![]() soit
soit ![]()
qui est un cas particulier de l'équation d'Euler (Mécanique
des fluides)
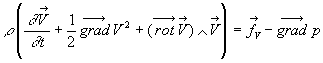
Equation de conservation de la masse (dite équation de continuité)
Sur la tranche en mouvement, on écrit que la différence
entre le flux de matière entrant et sortant est égale à
l’accroissement, par unité de temps, de matière dans la tranche
:
![]() (
(![]() )
)
soit, en appliquant la formule des accroissements finis, ![]() [formule qui est un cas particulier de
[formule qui est un cas particulier de ![]() ].
].
La faiblesse des quantités ![]() permet la simplification (appelée approximation acoustique) des
deux expressions ci-dessus sous la forme :
permet la simplification (appelée approximation acoustique) des
deux expressions ci-dessus sous la forme :
![]() et
et ![]()
En introduisant ![]() ,
soit
,
soit ![]() , on
obtient
, on
obtient ![]() et
et
![]()
Par dérivation, on découple le système précédent
en :
![]() et
et ![]()
Pour ce qui est du déplacement s, on peut l’introduire par la
relation ![]() et
obtenir
et
obtenir ![]() ou
utiliser
ou
utiliser ![]() .
.
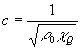 est la vitesse
de phase de l’onde
est la vitesse
de phase de l’onde
Remarque : pour un gaz parfait, ![]() soit
soit 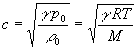
1.2. Impédance de l'onde acoustique
Par définition, on appelle impédance acoustique caractéristique
de l'onde acoustique la quantité ![]()
L’impédance acoustique est définie par la relation ![]() .
.
Les solutions générales des équations de propagation
s'écrivent :
![]() et
et ![]()
En considérant séparément l'onde progressive et
l'onde régressive, on peut écrire la relation
![]() où
où ![]() est la résistivité caractéristique de l’onde acoustique
progressive ou régressive.
est la résistivité caractéristique de l’onde acoustique
progressive ou régressive.
1.3. Energie de l'onde acoustique progressive
La force ![]() agit sur face x qui se déplace à vitesse u.
agit sur face x qui se déplace à vitesse u.
L’énergie fournie à la tranche est donc : ![]() .
.
Pour une onde acoustique progressive, on obtient ![]() où
où ![]() représente le volume balayé par l’onde pendant le temps dt,
c’est à dire le volume où a été emmagasiné
le travail des forces due à la perturbation de pression.
représente le volume balayé par l’onde pendant le temps dt,
c’est à dire le volume où a été emmagasiné
le travail des forces due à la perturbation de pression.
Ainsi la densité volumique d’énergie e est égale
à ![]()
Cette énergie, dans la tranche dx, est emmagasinée
:
- sous forme cinétique,![]() dont la densité volumique est
dont la densité volumique est ![]()
- sous forme de travail des forces de pression qui provoquent les variations
de volume de cette tranche (énergie interne), 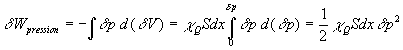 dont la densité volumique est
dont la densité volumique est ![]() .
.
Pour une onde progressive, ![]() (exemple d'équipartition de l'énergie).
(exemple d'équipartition de l'énergie).
L'intensité acoustique I est le flux énergétique
de l'onde à travers une surface unitaire ð![]() pour l’onde progressive.
pour l’onde progressive.
Plus souvent, on caractérise cette intensité par son niveau défini
par la relation ![]() exprimée en décibels où
exprimée en décibels où ![]() correspond au seuil conventionnel de sensibilité de l'oreille.
correspond au seuil conventionnel de sensibilité de l'oreille.
Pour une conversation normale entre deux personnes situées à 1
m l'une de l'autre, le niveau sonore est de 60 dB (soit ![]() ).
).
Un niveau sonore de 120 dB est douloureux et dangereux.
2. La corde vibrante " infiniment souple "
La corde est dénuée de coefficient de raideur, c'est à
dire que le système de forces en un point de la corde se réduit
à une force unique appelée tension T
de la corde, tangente à la direction de la corde.
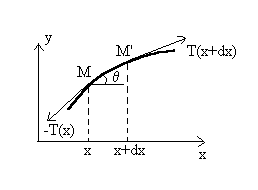 |
Sur la corde dont les seuls mouvements (faibles)
sont transversaux à l'axe des x (par exemple suivant l'axe
y),
on considère deux points voisins M et M' dont les
coordonnées sont :
[ La longueur de l'arc MM' est : |
Si ![]() est la
masse linéique de la corde, la projection de l'équation fondamentale
de la dynamique suivant l'axe des x s'écrit :
est la
masse linéique de la corde, la projection de l'équation fondamentale
de la dynamique suivant l'axe des x s'écrit :
![]() car l'angle
car l'angle![]() reste petit (
reste petit ( ![]() est équivalent à 1 au 2ème ordre près). Par suite,
est équivalent à 1 au 2ème ordre près). Par suite, ![]()
La projection de l'équation fondamentale de la dynamique suivant
l'axe des y s'écrit :
![]()
![]() est équivalent
à
est équivalent
à ![]() et
à
et
à ![]()
En remplaçant ![]() ð
ð![]()
![]() est la vitesse
de phase de l’onde.
est la vitesse
de phase de l’onde.
2.2. Energie
L'énergie cinétique est égale à ![]() soit par unité de longueur
soit par unité de longueur ![]()
L'allongement de la portion dx au repos est égal à ![]() si bien que l'énergiepotentielle par unité de longueur
est
si bien que l'énergiepotentielle par unité de longueur
est ![]()
L'énergie totale par unité de longueur est ![]() .
.
Pour l'onde progressive, on retrouve ![]() .
.