Généralités sur les phénomènes
de propagation
Les exemples de phénomènes de propagation sont multiples
: nous parlons de propagation de la lumière, d’ondes électromagnétiques,
du son ou de la "chaleur" sans que ces phénomènes soient
de même nature.
Les ondes électromagnétiques (nous verrons que l'onde
lumineuse est une onde électromagnétique de longueurs d'ondes
inférieures à 100 mm) se
propagent dans le vide, se réfléchissent, s'absorbent et
se transmettent au niveau d'un milieu matériel.
Les ondes mécaniques (qui comprennent le son -ondes acoustiques-)
ont besoin d'un milieu matériel pour se propager.
La propagation de la "chaleur" est plus complexe : c'est une onde électromagnétisme
dans le cas du rayonnement dit "thermique", une onde mécanique dans
le cas de la conduction de la chaleur et un transfert de matière
dans le cas de la convection.
Mathématiquement, deux équations aux dérivées
partielles rendent compte de ce type de phénomènes :
-
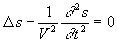 dite équation
hyperbolique ou de D'Alembert
dite équation
hyperbolique ou de D'Alembert
-
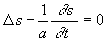 dite équation
parabolique. Cette équation est plus souvent appelée équation
de diffusion par les physiciens : elle régit la conduction de la chaleur,
la diffusion de matière.
dite équation
parabolique. Cette équation est plus souvent appelée équation
de diffusion par les physiciens : elle régit la conduction de la chaleur,
la diffusion de matière.
Nous limitons nos propos à l’équation de propagation hyperbolique
à une dimension 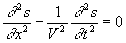 .
.
On montrera (paragraphe 1) que cette équation représente,
sur le plan mathématique, la propagation sans déformation
d’une quantité s appelée onde par les physiciens.
L’onde s peut être scalaire ou vectorielle, dans ce dernier
cas on est conduit à trois relations scalaires. Elle peut avoir
un caractère longitudinal (de même "sens" que l'axe x)
ou transversal (perpendiculaire à l'axe x).
Le mouvement de la surface de l'eau après l'avoir frappé
est un exemple d'onde facilement observable. La matière se déplace
verticalement alors que les rides se propagent horizontalement (ce type d'onde
est qualifiée de transversale). Il apparaît deux déplacements,
l'un (celui de la matière) à vitesse faible, l'autre (celui des
rides) à vitesse importante que l'on nommera vitesse V
de l'onde. En frappant périodiquement la surface ( source vibrante),
on entretient le mouvement.
L'onde sonore est un exemple d'onde longitudinale, c'est à
dire où les déplacements de matière autour d'une position
d'équilibre ont lieu dans la même direction que le déplacement
de l'onde.
1. Intégrale générale
de l’équation de propagation
Pour résoudre l’équation hyperbolique, nous effectuons les changements
de variables 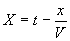 et
et 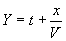 et cherchons
et cherchons 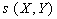 .
.
La substitution dans l’équation de propagation conduit à 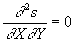 qui est réalisé si
qui est réalisé si 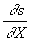 est indépendant de Y et
est indépendant de Y et 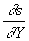 indépendant de X.
indépendant de X.
Par suite 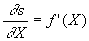 ,
, 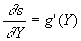 et
et 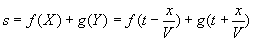 où les fonctions f et g sont arbitraires.
où les fonctions f et g sont arbitraires.
La fonction f qui prend une valeur 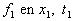 reprend cette même valeur
reprend cette même valeur 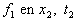 (ce qui est caractéristique de la propagation sans déformation
de la quantité f de l’abscisse
(ce qui est caractéristique de la propagation sans déformation
de la quantité f de l’abscisse 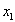 à l’abscisse
à l’abscisse 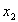 )
si
)
si 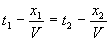 soit encore
soit encore 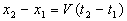 .
.
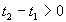 ð
ð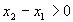 .
La propagation a lieu, à vitesse V, dans la direction des x
positifs.
.
La propagation a lieu, à vitesse V, dans la direction des x
positifs.
Ainsi le groupement 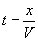 exprime que l'onde traduite par la fonction f se propage sans
déformation à vitesse V dans la direction des x
positifs (on dit onde positive ou progressive) et le groupement
exprime que l'onde traduite par la fonction f se propage sans
déformation à vitesse V dans la direction des x
positifs (on dit onde positive ou progressive) et le groupement 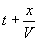 exprime que l'onde traduite par la fonction g se propage sans déformation
à vitesse V dans la direction des x négatifs (on
dit onde négative ou régressive).
exprime que l'onde traduite par la fonction g se propage sans déformation
à vitesse V dans la direction des x négatifs (on
dit onde négative ou régressive).
L’onde s est la superposition des deux propagations dites positive
(progressive) et négative (régressive).
1.1. Signification des fonctions f et
g
Soit une source émettant au point 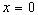 dans la direction des x positifs. On ne voit pas d’où proviendrait
la fonction g tant que l’on considère le milieu infini suivant
les x, mais s’il y a un obstacle en un point
dans la direction des x positifs. On ne voit pas d’où proviendrait
la fonction g tant que l’on considère le milieu infini suivant
les x, mais s’il y a un obstacle en un point 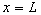 une partie de l’onde sera renvoyée (réfléchie) vers les
x négatifs et on aura, en tout point, la superpositions des deux
propagations.
une partie de l’onde sera renvoyée (réfléchie) vers les
x négatifs et on aura, en tout point, la superpositions des deux
propagations.
La fonction g est déterminée à partir de la fonction
f par les conditions à l’extrémité L. Le
cas particulier 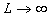 impose
impose .
.
La fonction f est déterminée par la nature de la source
en 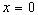 . L’expression
. L’expression 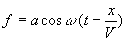 associée à une source de type vibratoire joue un rôle privilégié.
En effet pour l’équation de propagation, de type linéaire, étudiée,
toute excitation peut être traitée à l’aide de la technique
mathématique des séries de Fourier ou de celle de la transformée
de Fourier à partir de cette fonction (voir annexe " Eléments
de Mathématiques ").
associée à une source de type vibratoire joue un rôle privilégié.
En effet pour l’équation de propagation, de type linéaire, étudiée,
toute excitation peut être traitée à l’aide de la technique
mathématique des séries de Fourier ou de celle de la transformée
de Fourier à partir de cette fonction (voir annexe " Eléments
de Mathématiques ").
Il est commode, d’un point de vue mathématique, d’introduire la notation
complexe 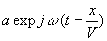 ,
la fonction f étant la partie réelle de
,
la fonction f étant la partie réelle de 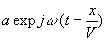 .
.
Si nous reprenons l'exemple de l'onde à la surface d'un liquide,
a représente l'amplitude du mouvement vertical de matière,
c’est à dire l'écartement maximal à la position d'équilibre.
La dérivée par rapport au temps de la fonction f
donne la vitesse de la matière. Cette vitesse est proportionnelle
à l'amplitude a.
Le carré de l’amplitude a est donc directement proportionnel
au carré de la vitesse de déplacement de la matière,
donc proportionnel à la puissance énergétique (intensité)
de l'onde.
Ceci constitue un résultat général pour toutes
les ondes matérielles ou non.
1.2. Périodicité temporelle. Périodicité
spatiale.
Si t et x deviennent 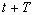 et
et 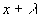 tels que
tels que 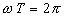 et
et 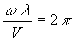 , la fonction
f est inchangée.
, la fonction
f est inchangée.
T , périodicité temporelle, est appelée période
et 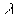 , périodicité
spatiale, est appelée longueur d’onde. Ces deux quantités
sont liées par la relation
, périodicité
spatiale, est appelée longueur d’onde. Ces deux quantités
sont liées par la relation 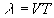 .
.
1.3. Ecriture générale de l'onde progressive.
Vecteur d'onde
- En introduisant la quantité
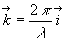 appelée vecteur d’onde, on obtient
appelée vecteur d’onde, on obtient 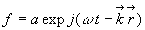 .
.
Cette écriture est intéressante par son caractère général
adapté à une propagation dans une direction de vecteur unitaire 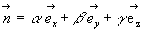 et
de vecteur d’onde
et
de vecteur d’onde 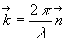 .
.
Elle permet d’écrire,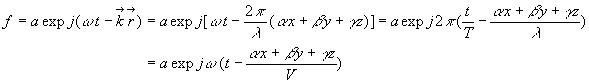
La quantité 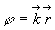 représente la phase de l’onde en un point quelconque de l’espace.
Les surfaces définies par
représente la phase de l’onde en un point quelconque de l’espace.
Les surfaces définies par 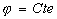 sont appelées surfaces équiphases ou surfaces d’onde.
sont appelées surfaces équiphases ou surfaces d’onde.
- D'une manière plus générale, la fonction
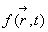 est le produit :
est le produit :
- d'une fonction 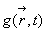 dans laquelle
dans laquelle  interviennent sous la forme d'un terme de propagation,
interviennent sous la forme d'un terme de propagation,
- d'une fonction 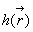 ,
dite fonction d'espace ;
,
dite fonction d'espace ; 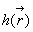 représente l'amplitude de l'onde, elle est indépendante de
représente l'amplitude de l'onde, elle est indépendante de 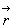 lorsque
l'onde est plane.
lorsque
l'onde est plane.
1.4. Propagation
libre et régimes stationnaires
En l’absence de limite 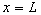 ,
la fonction g est nulle et la fonction f s’écrit :
,
la fonction g est nulle et la fonction f s’écrit :
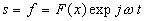 pour une propagation
suivant la direction x.
pour une propagation
suivant la direction x.
 .
.
Si, par contre, la limite 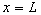 renvoie partiellement ou totalement l’onde f, alors la fonction g
est non nul et
renvoie partiellement ou totalement l’onde f, alors la fonction g
est non nul et 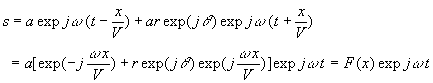
où 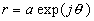 représente
le facteur de réflexion en
représente
le facteur de réflexion en 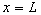 .
.
Pour une réflexion totale [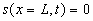 ],
], 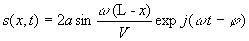
Dans ce cas, on dit que l’on a un régime stationnaire car le
phénomène de propagation n'existe plus.
Si, en 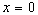 , existe
une autre réflexion totale, on se trouve en présence d’un régime
stationnaire confiné entre deux réflexions totales. Ce type de
régime stationnaire est appelé régime résonnant
qui ne peut exister que pour certaines valeurs discrètes
, existe
une autre réflexion totale, on se trouve en présence d’un régime
stationnaire confiné entre deux réflexions totales. Ce type de
régime stationnaire est appelé régime résonnant
qui ne peut exister que pour certaines valeurs discrètes 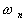 de
de 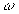 appelés
en mathématiques valeurs propres et en physique pulsations
de résonance. Les fonctions
appelés
en mathématiques valeurs propres et en physique pulsations
de résonance. Les fonctions 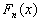 correspondantes sont appelées fonctions propres.
correspondantes sont appelées fonctions propres.
2. Propagation dans un milieu dispersif
Le cas d’une onde sinusoïdale pure de pulsation 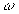 est
un cas extrêmement rare dans la réalité, il doit être
considéré comme un cas d’école.
est
un cas extrêmement rare dans la réalité, il doit être
considéré comme un cas d’école.
En fait, la forme du signal jointe à sa durée conduisent à
une représentation de celui-ci, dans l’échelle des 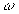 ,
par un spectre.
,
par un spectre.
Si la vélocité du phénomène V n’est pas fonction
de 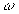 , chaque
composante spectrale se propage à cette vitesse et, à l’arrivée,
toutes les composantes peuvent être regroupées de façon
identique au départ : le signal n’est pas déformé (à
condition qu’il n’y ait pas d’atténuations ou que celles-ci soient indépendantes
de
, chaque
composante spectrale se propage à cette vitesse et, à l’arrivée,
toutes les composantes peuvent être regroupées de façon
identique au départ : le signal n’est pas déformé (à
condition qu’il n’y ait pas d’atténuations ou que celles-ci soient indépendantes
de 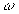 ).
).
Il en va autrement si V dépend de 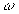 .
Ces phénomènes sont bien connus dans le cas de la lumière
où on dit qu’il y a dispersion.
.
Ces phénomènes sont bien connus dans le cas de la lumière
où on dit qu’il y a dispersion.
2.1. Cas de la propagation de deux ondes
Les deux ondes, émises en 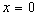 ,
supposées pour simplifier de même amplitude a, de pulsations
voisines
,
supposées pour simplifier de même amplitude a, de pulsations
voisines 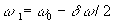 et
et 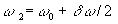 , se propagent
dans la direction des x positifs.
, se propagent
dans la direction des x positifs.
A partir de 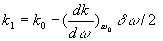 et
et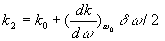 [où
[où 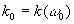 ]
, le calcul de l’onde totale conduit à
]
, le calcul de l’onde totale conduit à 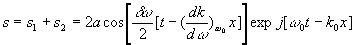
On retrouve la fonction d’onde habituelle avec une amplitude variable
c’est à dire dépendant de t et x.
Si l’on se place dans un référentiel d’observation se mouvant,
suivant l’axe des x, à la vitesse 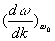 ,
l’amplitude apparaît constante.
,
l’amplitude apparaît constante.
Cette vitesse 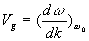 est appelée vitesse de groupe. Liée à l’amplitude,
elle traduit la vitesse de propagation de l’énergie.
est appelée vitesse de groupe. Liée à l’amplitude,
elle traduit la vitesse de propagation de l’énergie.
La vitesse 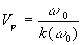 est appelée vitesse de phase.
est appelée vitesse de phase.
Une autre façon d’analyser la fonction d’onde est de considérer
que 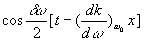 sert
d’enveloppe à la fonction d’onde habituelle et de faire apparaître
un phénomène de battement qui se déplace à la vitesse
sert
d’enveloppe à la fonction d’onde habituelle et de faire apparaître
un phénomène de battement qui se déplace à la vitesse 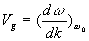 .
.
2.2. Ondes d'extension limitée : paquet d'ondes
On envisage le modèle simplifié d'ondes planes sinusoïdales,
de même amplitude a, dans un intervalle continu de pulsation 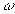 tel que :
tel que : 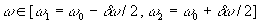 avec
avec 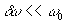 se propageant
dans la direction des x positifs (ondes progressives).
se propageant
dans la direction des x positifs (ondes progressives).
L'onde résultante est égale à :
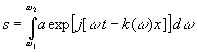
Un développement limité au premier ordre permet d'écrire
la fonction k :
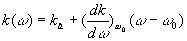
En remplaçant dans l'onde résultante et en intégrant,
on obtient :
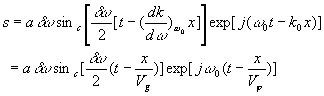
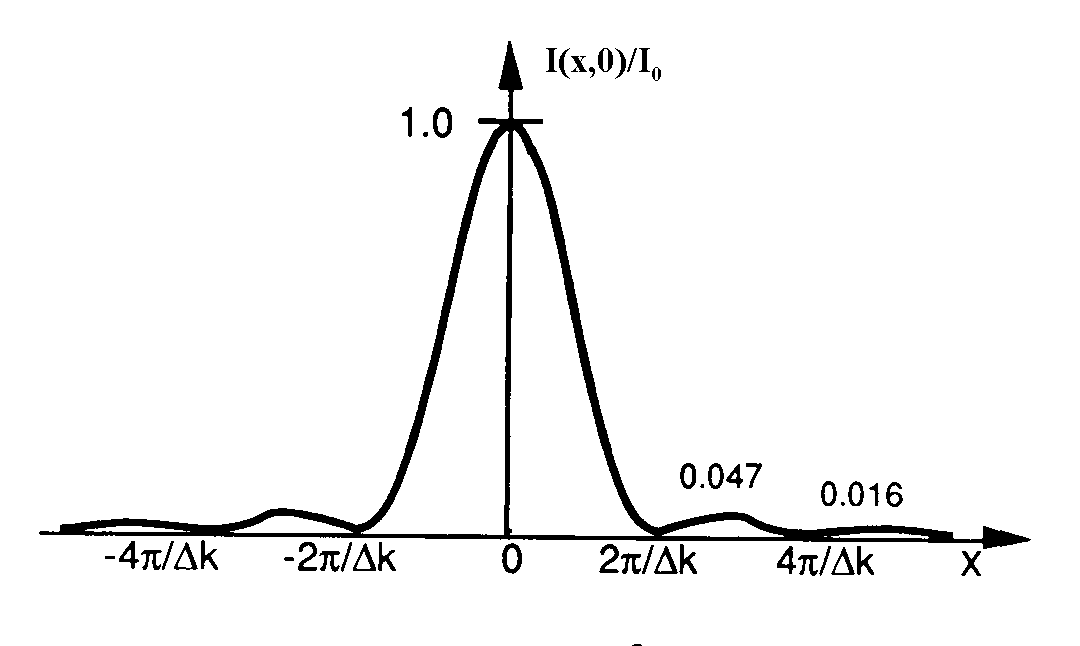
Ce graphe appelle plusieurs commentaires :
- les amplitudes des maxima secondaires sont très faibles vis à
vis du maximum central (en 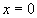 ),
),
- le paquet d'ondes simule donc un phénomène de propagation d'étendue 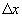 limitée ; on fixe la largeur du maximum central comme le domaine de variation
de x compris entre
limitée ; on fixe la largeur du maximum central comme le domaine de variation
de x compris entre 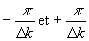 ,
soit
,
soit  . Aux
frontières du domaine,
. Aux
frontières du domaine, 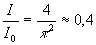 ,
,
- le maximum de I est atteint au temps 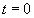 lorsque
lorsque 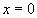 . Si
. Si 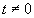 ,
ce maximum est atteint pour
,
ce maximum est atteint pour 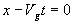 ð
il se déplace à la vitesse
ð
il se déplace à la vitesse 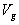 qui
est la vitesse de propagation de l'énergie puisque l'intensité
du paquet d'onde se situe autour du maximum central,
qui
est la vitesse de propagation de l'énergie puisque l'intensité
du paquet d'onde se situe autour du maximum central,
- l'onde monochromatique (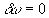 )
correspond donc à une extension spatiale illimitée (
)
correspond donc à une extension spatiale illimitée (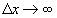 )
: correspondant à une énergie infinie, elle ne peut avoir un sens
physique réel et doit être comprise comme une limite théorique.
)
: correspondant à une énergie infinie, elle ne peut avoir un sens
physique réel et doit être comprise comme une limite théorique.
2.3. Remarque
La vitesse de groupe a un sens physique puisqu ‘elle représente
la vitesse de propagation de l’énergie, soit aussi de l’information
; pour les ondes électromagnétiques dans le vide, elle ne
pourra dépasser la " vitesse de la lumière c " ; la
vitesse de phase n’a pas de réalité physique, elle pourra,
dans le cas des ondes électromagnétiques, être supérieure
à celle de la lumière.
Le cas 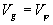 ð
ð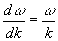 soit
soit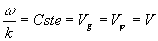 correspond
à une propagation d'ondes sans dispersion.
correspond
à une propagation d'ondes sans dispersion.
3. Régimes quasi-stationnaires
Le groupement 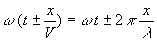 ,
où
,
où 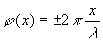 est la phase, joue un rôle privilégié. Dans un espace de
dimension
est la phase, joue un rôle privilégié. Dans un espace de
dimension 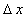 ,
la variation de phase s'écrit
,
la variation de phase s'écrit 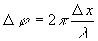 .
.
Dans le cas particulier où 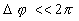 (soit aussi
(soit aussi 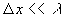 ),
les variations de phase sont négligeables, la fonction ne dépend
plus de x, le phénomène de propagation est négligeable,
la notion d'onde disparaît.
),
les variations de phase sont négligeables, la fonction ne dépend
plus de x, le phénomène de propagation est négligeable,
la notion d'onde disparaît.
Ceci s'appelle l'approximation des régimes (ou états)
quasi-stationnaires, bien connue en Electricité des courants
alternatifs.
Ainsi, pour le 50 Hz, dans un milieu non diélectrique et non magnétique
(le "vide"), 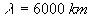 .
.
4. Effet Doppler-Fizeau 
Doppler a montré, pour les ondes acoustiques, que la période
est relative au référentiel où elle est mesurée.
Fizeau a élargi ce phénomène au domaine de l'optique.
La théorie doit être faite dans le cadre de la cinématique
relativiste si les vitesses des référentiels n'étaient
pas négligeables devant celle de la lumière.
Nous nous limitons au domaine classique des " faibles " vitesses, cependant
la théorie relativiste est importante car sa confirmation expérimentale
valide cette théorie et les idées émises par Einstein.
Calcul de Doppler (cinématique classique)
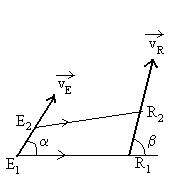 |
Un émetteur E se déplace à
vitesse 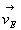 en
émettant de signaux de période en
émettant de signaux de période 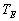 . .
Ces signaux se propagent uniformément dans toutes les directions
à intensité de vitesse V.
Un récepteur R se déplace à vitesse 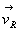 recevant les signaux avec une période
recevant les signaux avec une période 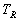 . .
Au temps 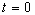 ,
l'émetteur est à la position ,
l'émetteur est à la position 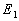 ,
le récepteur reçoit à la position ,
le récepteur reçoit à la position 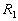 au temps
au temps 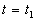 . . |
Au temps 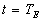 ,
l'émetteur est à la position
,
l'émetteur est à la position 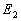 ,
le récepteur reçoit à la position
,
le récepteur reçoit à la position 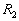 au temps
au temps 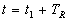 .
.
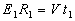 ;
; 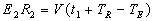 ;
; 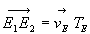 ;
; 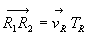
Dans un repère d'origine  ,
d'axe des x parallèle à
,
d'axe des x parallèle à  ,
on écrit les coordonnées :
,
on écrit les coordonnées :
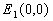 ;
; 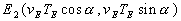 ;
; 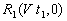 ;
; 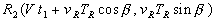
En écrivant la longueur 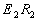 des deux manières possibles et en réorganisant, on obtient :
des deux manières possibles et en réorganisant, on obtient :
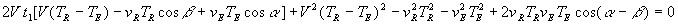 pour laquelle
il convient de chercher une solution indépendante de
pour laquelle
il convient de chercher une solution indépendante de 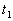 c'est à dire de l'émission initiale considérée.
c'est à dire de l'émission initiale considérée.
- Une solution rigoureuse correspond à
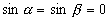 (pour
(pour 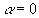 , le
récepteur s’éloigne de l’émetteur si
, le
récepteur s’éloigne de l’émetteur si 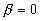 ; il s’en rapproche si
; il s’en rapproche si 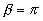 ).
).
Sous ces conditions, on obtient alors 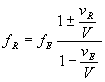 formule de Doppler écrite en introduisant les fréquences
formule de Doppler écrite en introduisant les fréquences 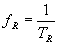 et
et 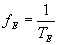 (le signe
– correspond à un éloignement du récepteur vis à
vis de l’émetteur, le signe + à un rapprochement).
(le signe
– correspond à un éloignement du récepteur vis à
vis de l’émetteur, le signe + à un rapprochement).
- Dans le cas habituel où la vitesse V de propagation de l’onde
est très supérieure aux vitesses de déplacement de l’émetteur
ou du récepteur,
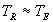 .
.
En négligeant tous les termes du second ordre, la seule condition 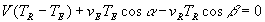 suffit et la formule de Doppler s’écrit sous la forme :
suffit et la formule de Doppler s’écrit sous la forme : 
L'effet Doppler est utilisé avec des ultrasons pour mesurer, par
exemple, des vitesses d'écoulement sanguin ou avec des ondes lumineuses
pour, par exemple, les contrôles de vitesse des véhicules.
Il permet aussi de connaître les vitesses des planètes de
l'Univers.
5. Interférences
Lorsque l'intensité résultant de la superposition de deux
ou plusieurs ondes n'est pas la somme des intensités de chacune
des ondes, on dit qu'il y a interférence ou que les ondes interfèrent.
L'interférence
est caractéristique d'un phénomène ondulatoire.
Conditions de réalisation d'une interférence
Le domaine de la lumière (des ondes électromagnétiques)
fournit un champ de réalisations très important. C'est pourquoi
il y sera fait référence de manière privilégiée.
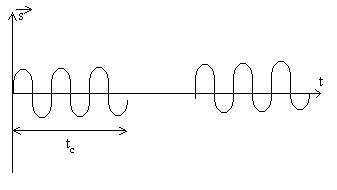 |
Les sources émettent de la lumière
par suite de la désexcitation des atomes qui ont été
préalablement excités.
Cette émission est lancée, interrompue puis relancée
au hasard des collisions entre les atomes.
On la représente sous la forme de trains d'onde successifs émis
de façon aléatoire. |
On caractérise cette émission par la fonction vectorielle 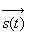 appelée
vibration lumineuse.
appelée
vibration lumineuse.
 pendant la
durée
pendant la
durée 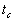 d'un train d'ondes largement inférieure à la durée moyenne
entre deux collisions successives (
d'un train d'ondes largement inférieure à la durée moyenne
entre deux collisions successives (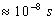 ).
).
L'intensité I associée à une telle onde est égale
à la valeur moyenne de l'intensité instantanée pendant
la durée 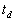 nécessaire
à la détection (
nécessaire
à la détection (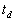 est de l'ordre de 0, 1 s).
est de l'ordre de 0, 1 s).

Pour les ondes mécaniques, la source vibrante entretient le
mouvement pendant la durée d'un train d'ondes, puis elle est relancée
pour un nouveau train d'ondes, ...
L'émission est caractérisée par une fonction scalaire 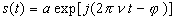
Interférence de deux ondes monochromatiques isochrones
Geneviève Tulloue [ 
 ] ; Jacques
Charrier
] ; Jacques
Charrier
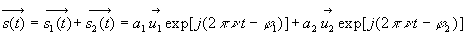 ð
ð
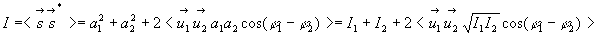
Pour une onde scalaire, il convient d'enlever tout caractère
vectoriel aux formules ci-dessus.
- Si nous considérons deux sources indépendantes, les phases
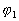 et
et 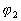 sont
aléatoires et indépendantes si bien que toutes les valeurs de
sont
aléatoires et indépendantes si bien que toutes les valeurs de 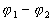 sont équiprobables dans l'intervalle [
sont équiprobables dans l'intervalle [ [
et
[
et 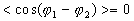 ð
ð 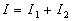 Il n'y a pas interférence
Il n'y a pas interférence
Une condition nécessaire pour obtenir des phénomènes
d'interférence est de neutraliser le caractère indépendant
de l'émission de deux sources. On y parvient en subordonnant les
deux sources a une même source primaire.
On dispose de deux types de système interférentiel :
ceux à division de front d'ondes et ceux à division d'amplitude
(ou incident unique).
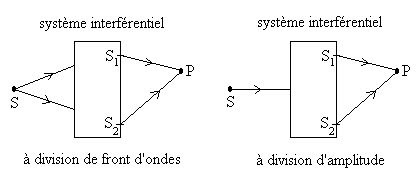
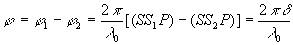 où
où 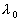 est la longueur d'onde et
est la longueur d'onde et 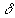 la différence de marche entre les deux chemins.
la différence de marche entre les deux chemins.
En fait, pour les ondes lumineuses, 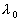 est la longueur d'onde dans le vide et
est la longueur d'onde dans le vide et 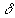 la différence de marche entre les chemins optiques.
la différence de marche entre les chemins optiques.
-
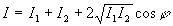 constitue
la formule de base dans les phénomènes d'interférence
à deux ondes (pour les ondes lumineuses c’est à dire à
caractère vectoriel, cette relation suppose les vecteurs
constitue
la formule de base dans les phénomènes d'interférence
à deux ondes (pour les ondes lumineuses c’est à dire à
caractère vectoriel, cette relation suppose les vecteurs 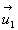 et
et 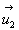 quasiment
parallèles.
quasiment
parallèles.
Suivant les valeurs de 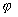 ,
l'intensité évolue d'une valeur minimale
,
l'intensité évolue d'une valeur minimale 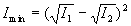 à une valeur maximale
à une valeur maximale 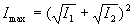 ,
elle n’est égale à
,
elle n’est égale à 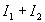 que pour des valeurs particulières de
que pour des valeurs particulières de 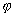 correspondant à
correspondant à 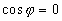 .
.
Entre un minimum et un maximum successif, la différence de phase est
égal à 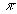 et la différence de marche à une demi longueur d'onde.
et la différence de marche à une demi longueur d'onde.
On définit le contraste (visibilité) par 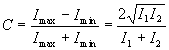 qui est maximum et égal à 100% si
qui est maximum et égal à 100% si 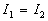 et tend vers 0 si
et tend vers 0 si 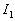 et
et 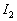 sont très différents.
sont très différents.
- L'interférence lumineuse étant réalisée (
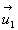 et
et 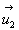 sont
quasiment parallèles), on fait disparaître ce phénomène
en intercalant, sur l'un des chemins, un polariseur dont l'action est de faire
tourner de 90 degrés la vibration lumineuse (
sont
quasiment parallèles), on fait disparaître ce phénomène
en intercalant, sur l'un des chemins, un polariseur dont l'action est de faire
tourner de 90 degrés la vibration lumineuse (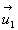 et
et 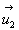 deviennent
perpendiculaires).
deviennent
perpendiculaires).
Ce type d'expérience, en montrant le caractère vectoriel
de la vibration lumineuse, a apporté une preuve déterminante
pour établir que l'onde lumineuse est une onde électromagnétique;
Cohérence spatiale [ Yves
Cortial ]
La figure d'interférence de la source étendue est la somme en
intensité des figures d'interférences des sources "ponctuelles"
constituant la source étendue.
Si les 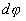 varient
de
varient
de 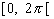 , il n'y
aura plus de figure d'interférences, les différentes sources ponctuelles
se contrariant , les maxima de l'une correspondant aux minima de l'autre.
, il n'y
aura plus de figure d'interférences, les différentes sources ponctuelles
se contrariant , les maxima de l'une correspondant aux minima de l'autre.
Une condition d'existence d'interférences est que  ,
valeur maximale de la variation de
,
valeur maximale de la variation de 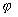 sur
toute l'étendue de la source reste très inférieure à .
sur
toute l'étendue de la source reste très inférieure à .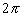
Si 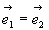 (incident
unique ou interférence à division d'amplitude), l'étendue
de la source ne pose pas de problème.
(incident
unique ou interférence à division d'amplitude), l'étendue
de la source ne pose pas de problème.
Pour la division de front d'ondes (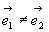 ),
il convient que la source soit "suffisamment ponctuelle".
),
il convient que la source soit "suffisamment ponctuelle".
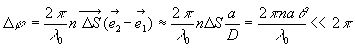 ð
ð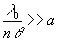
La quantité 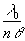 est appelée la largeur de cohérence spatiale.
est appelée la largeur de cohérence spatiale.
Cohérence temporelle [ Yves
Cortial ]
Les ondes émises par une source ne sont jamais parfaitement monochromatiques.
Pour les ondes lumineuses, la principale cause étant l'effet Doppler
résultant de l'agitation thermique.
L'intensité spectrale est définie par la relation 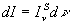 où
dI est l'intensité sur la bande spectrale
où
dI est l'intensité sur la bande spectrale 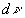 .
.
- Un autre processus pour appréhender cette question est de s'interroger
sur la durée d'émission.
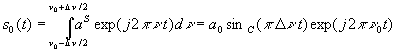 avec
avec 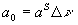 (
(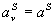 représente
l'amplitude de la vibration prise constante dans la bande spectrale considérée
et
représente
l'amplitude de la vibration prise constante dans la bande spectrale considérée
et 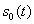 la vibration
émise).
la vibration
émise).
Au delà du temps 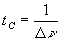 ,
la vibration devient très faible et on peut considérer que la
source n'émet plus. Dans cette interprétation,
,
la vibration devient très faible et on peut considérer que la
source n'émet plus. Dans cette interprétation,  est la durée de l'émission.
est la durée de l'émission.
On trouve là un résultant important : seule la source
monochromatique a une durée d'émission illimitée.
Evidemment, il ne peut s'agir que d'un cas limite d'école.
 |
Soient 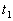 le temps que met l'onde pour parcourir SP par le chemin (1) et
le temps que met l'onde pour parcourir SP par le chemin (1) et 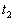 le temps par le chemin (2).
le temps par le chemin (2).
Nous raisonnons avec 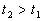 ,
par suite ,
par suite 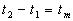 représente la différence des temps de marche.
représente la différence des temps de marche.
Le signal émis par la source S est perçu entre 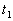 et
et 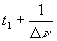 pour
le chemin (1), entre pour
le chemin (1), entre 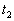 et
et 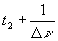 pour
le chemin (2). pour
le chemin (2). |
Pour qu'il y ait interférence, il convient que 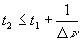 ,
soit
,
soit 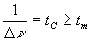 soit
la durée d'émission (appelée temps de cohérence)
supérieure à la différence des temps de marche.
soit
la durée d'émission (appelée temps de cohérence)
supérieure à la différence des temps de marche.
On introduit généralement la longueur de cohérence
définie par 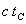 et, pour qu'il y ait interférence, il convient qu'elle soit supérieure
à la différence de marche.
et, pour qu'il y ait interférence, il convient qu'elle soit supérieure
à la différence de marche.
Des temps de cohérence (ou des durées d'émission) importants,
c'est à dire des sources les plus monochromatiques possibles, favorisent
le phénomène d'interférence.
Fonction
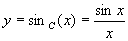 (prononcer
sinus cardinal de x)
(prononcer
sinus cardinal de x)
C’est une fonction paire.
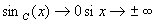 ;
; 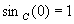
Cette fonction s’annule pour 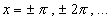
La dérivée est égale à 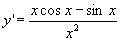 .
Elle s’annule pour
.
Elle s’annule pour 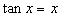 ,
soit pour
,
soit pour 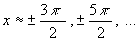 ; les valeurs correspondantes des extrema sont respectivement
; les valeurs correspondantes des extrema sont respectivement 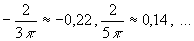
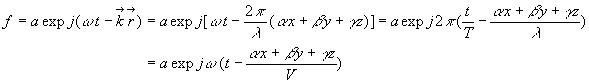
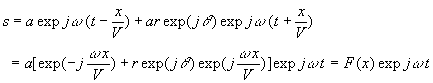
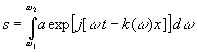
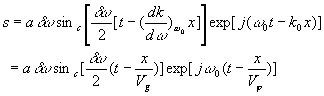

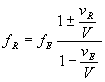 formule de Doppler écrite en introduisant les fréquences
formule de Doppler écrite en introduisant les fréquences 



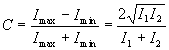 qui est maximum et égal à 100% si
qui est maximum et égal à 100% si 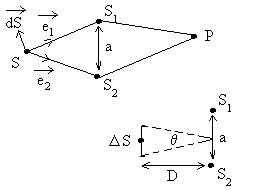
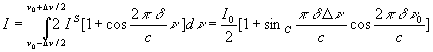 avec
avec 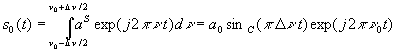 avec
avec 