Sur un élément de circuit
Sur un élément de circuit
La matière en présence d'un champ magnétique
Plan
1. Forces de Laplace. Loi de Biot et Savart
1.1. Forces de Laplace
1.2. Loi de Biot et Savart
1.3. Propriétés du champ magnétique
1.4. Energie potentielle
2. Le phénomène d'induction
2.1. Expériences significatives
2.2. Etude théorique quantitative
3. Les milieux magnétiques
3.1. Dipôle magnétique
3.2. Aimantation. Excitation magnétique
3.3. Potentiel vecteur créé par une aimantation
3.4. Théorème d'Ampère
3.5. Energie magnétique
4. Conséquences du phénomène d'induction
4.1. Exemple élémentaire de transformation énergie
électrique - énergie mécanique
4.2. Auto-induction. Induction mutuelle
4.3. Retour sur l'énergie magnétique
Lorsque deux circuits parcourus par des courants électriques constants
sont placés au " voisinage " l'un de l'autre, ils sont soumis à
des actions. L'étude de ces actions est le domaine de la magnétostatique.
La densité volumique de charges dans un conducteur parcouru par un courant
constant est nul si bien que l'origine des forces ne peut être attribué
à l'existence de champs électriques.
Enfin ce phénomène ne se limite pas aux circuits électriques,
les substances aimantées sont le siège d'interactions de
même nature.
1. Forces de Laplace. Loi de Biot et Savart
Résultats expérimentaux
 |
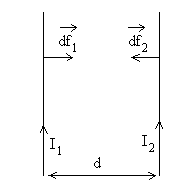
On considère deux fils rectilignes parallèles
de longueur " infinie " parcourus par des courants continus Sur un élément de circuit Sur un élément de circuit |
Les fils s'attirent si les courants sont de même sens et se repoussent
dans le cas contraire.
Cette formule est importante, elle sert à la définition de l'unité
d'intensité électrique l'ampère.
Deux fils rectilignes indéfinis distants de 1 m, parcourus par
des intensités électriques de 1 A exercent entre eux sur
des portions de 1 m des forces égales à ![]() .
Cette définition revient à dire que
.
Cette définition revient à dire que ![]() ,
perméabilité magnétique du vide, est égale à
,
perméabilité magnétique du vide, est égale à ![]() .
.
1.1. Forces magnétiques dites de Laplace
Une façon générale de présenter les forces qui
s'exercent entre circuits électriques est de considérer qu'un
circuit électrique 1 crée en tout point de l'espace un champ (induction)
magnétique ![]() tel que, sur un élément filiforme
tel que, sur un élément filiforme ![]() d'un circuit 2 parcouru par un courant
d'un circuit 2 parcouru par un courant ![]() ,
il s'exerce une force
,
il s'exerce une force ![]() .
Ce résultat est connu sous le nom de Force de Laplace.
.
Ce résultat est connu sous le nom de Force de Laplace.
Le champ ![]() fait
l'objet de la loi de Biot et Savart obtenue en généralisant les résultats expérimentaux
de l'interaction de deux fils rectilignes parallèles.
fait
l'objet de la loi de Biot et Savart obtenue en généralisant les résultats expérimentaux
de l'interaction de deux fils rectilignes parallèles.
Pour un circuit, il convient d'intégrer à tous les éléments
du circuit, il convient aussi de calculer le moment des forces.
Dans le cas d'un particule de charge q animée d'une vitesse ![]() dans un champ magnétique
dans un champ magnétique ![]() ,
la force de Laplace s'écrit
,
la force de Laplace s'écrit ![]() .
.
La loi de Biot et Savart donne l'expression du champ magnétique
créé, en tout point de l'espace, par un circuit électrique
filiforme parcouru par un courant ![]() ,
à savoir
,
à savoir 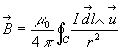 (
(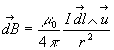 ).
).
Pour une particule de charge q animée d'une vitesse ![]() ,
la loi de Biot et Savart s'écrit
,
la loi de Biot et Savart s'écrit 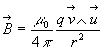 .
.
Dans la loi de Biot et Savart, ![]() représente le vecteur unitaire et r la distance entre l'élément
représente le vecteur unitaire et r la distance entre l'élément ![]() (où la charge est en mouvement) et le point où on considère
le champ magnétique.
(où la charge est en mouvement) et le point où on considère
le champ magnétique.
Pour des distributions volumiques ou surfaciques de courant, l'expression de
la force de Laplace et la loi de Biot et Savart doivent être réécrites.
Les termes ![]() deviennent
deviennent ![]() pour un courant volumique et
pour un courant volumique et ![]() pour un courant surfacique, les intégrations seront à faire suivant
le volume du conducteur ou sa surface.
pour un courant surfacique, les intégrations seront à faire suivant
le volume du conducteur ou sa surface.
Le champ magnétique est créé par des charges en mouvement et agit sur des charges en mouvement.
1.2.1. Remarque sur la loi de Biot et Savart. Forces électromagnétiques dites de Lorentz
La notion de mouvement est relative. Dans la présentation de la loi
de Biot et Savart, on s'est placé dans un référentiel 1
où le conducteur est immobile et on a considéré le mouvement
de charges positives fictives (en fait le mouvement est celui de charges électriques
de vitesses opposées et de charges opposées - électrons
libres -). Nous aurions pu considérer un référentiel lié
aux charges positives fictives, le conducteur (donc les ions positifs) aurait
été en mouvement et c'est à ce mouvement de charges qu'aurait
été attribuée l'origine du champ magnétique.
Prenons le cas d’une seule charge en mouvement dans un référentiel
1, elle crée, en tout point de l'espace, un champ magnétique ![]() et un champ électrique
et un champ électrique ![]() .
.
Plaçons nous dans un référentiel 0 lié à
la charge. Nous sommes ramenés à un problème d'électrostatique
et la charge immobile crée, en tout point de l'espace, un champ électrostatique
coulombien ![]() .
.
En Relativité on résout le problème du passage du
référentiel 0 au référentiel 1. A ce stade, nous
nous contenterons de dire, qu'en négligeant les propagations c'est à
dire la vitesse de la charge devant la vitesse c de propagation des interactions
dans le vide, on trouve pour ![]() l'expression du champ coulombien et pour
l'expression du champ coulombien et pour ![]() la loi de Biot et Savart.
la loi de Biot et Savart.
Si, dans un référentiel, coexistent un champ électrique
![]() et un champ magnétique
et un champ magnétique ![]() ,
une charge électrique q est soumise à la superposition
des forces électrique et magnétique dite force électromagnétique
de Lorentz égale à
,
une charge électrique q est soumise à la superposition
des forces électrique et magnétique dite force électromagnétique
de Lorentz égale à ![]()
1.3. Propriétés du champ magnétique
Le champ magnétique obéit à deux propriétés que nous ne démontrons pas.
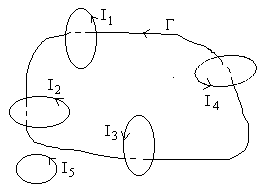 |
Sous sa forme intégrale, il s'exprime
:
|
Dans l'exemple de la figure ![]()
Localement le théorème d'Ampère s'écrit ![]() (application du théorème de Stokes pour passer d'une forme à
l'autre).
(application du théorème de Stokes pour passer d'une forme à
l'autre).
1.3.1. Potentiel vecteur ![]() .
Relation de jauge de Coulomb
.
Relation de jauge de Coulomb
La relation ![]() entraîne
l'existence d'un vecteur
entraîne
l'existence d'un vecteur ![]() ,
appelé potentiel vecteur, défini par
,
appelé potentiel vecteur, défini par ![]() .
.
On remarquera que le potentiel vecteur n'est pas défini de manière
unique. Connaissant un potentiel vecteur vérifiant la relation de définition,
on peut former un autre potentiel vecteur ![]() en ajoutant à
en ajoutant à ![]() le gradient
d'une fonction scalaire quelconque.
le gradient
d'une fonction scalaire quelconque.
On dit que ![]() n'est défini
qu'à un gradient additif près.
n'est défini
qu'à un gradient additif près.
En reportant le potentiel vecteur dans l'expression locale du théorème
d'Ampère, on obtient :
![]()
La jauge de Coulomb (qui entre dans le cadre plus générale
de la jauge de Lorentz) consiste à chercher (nous ne donnons pas la démonstration,
purement mathématique, sur la validité à faire cela) une
solution ![]() avec la condition
supplémentaire
avec la condition
supplémentaire ![]() .
.
Ainsi le potentiel vecteur obéit à l'équation aux dérivées
partielles ![]() qui donne trois relations scalaires analogues à
qui donne trois relations scalaires analogues à ![]() .
.
Pour un circuit filiforme parcouru par un courant I, le potentiel vecteur
s'écrit 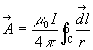
Pour des courants surfaciques ou volumiques, on peut écrire des formules
analogues en introduisant ![]() ou
ou ![]() .
.
1.3.2. Exemples de calcul du champ magnétique
En magnétostatique, il existe un certain nombre d'exercices
incontournables pour une bonne compréhension des idées. Sans
être exhaustif, nous citerons :
-le champ magnétique créé par un fil rectiligne de longueur
infinie et son flux à travers une spire rectangulaire,
- le champ magnétique sur l'axe d'une spire et sa circulation
suivant un contour fermé comprenant l'axe de la spire,
- le champ magnétique créé par un solénoïde
à spires jointives de longueur finie ou infinie,
- le potentiel vecteur d'un champ magnétique uniforme,
- le champ magnétique et le potentiel vecteur d'une nappe
volumique de courant, d'une nappe surfacique,
- le dipôle magnétique.
Soit un circuit ( C ) parcouru par un courant I , placé dans
un champ magnétique ![]() .
.
La force de Laplace s'écrit : ![]() .
.
Imaginons un déplacement élémentaire ![]() d'un point M quelconque du circuit. Le travail de la force de Laplace
sera :
d'un point M quelconque du circuit. Le travail de la force de Laplace
sera : ![]()
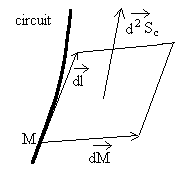 |
|
Ce flux est appelé flux coupé.
Calcul du flux coupé
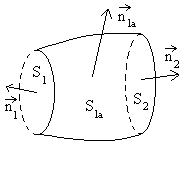 |
Nous considérons un circuit initialement
en position 1 (surface Le flux coupé est égal à |
Or ![]() ð
ð![]()
On dispose de deux méthodes pour calculer le flux coupé,
à partir de la définition ou en calculant la variation du
flux du champ magnétique entre la position initiale du circuit et
la position finale.
Pour un déplacement du circuit ( C ) entre deux positions notées
1 et 2.
![]()
Ce travail ne dépend que de la position initiale et finale, il est indépendant
du déplacement réel ð il existe
une énergie potentielle appelée magnétique ![]()
2.1. Expériences significatives
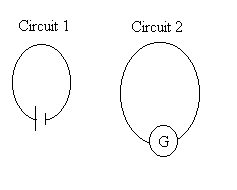 |
On considère deux circuits, le circuit
1 est alimenté par un générateur, le circuit 2 n'est
pas alimenté mais possède un galvanomètre pour détecter
un courant.
Nous avons dessiné des circuits à une spire, en fait des circuits à plusieurs spires (solénoïdes) produisent des résultats quantitatifs plus significatifs. 1) nous éloignons les circuits l'un de l'autre, le galvanomètre détecte un courant dans le circuit 2 pendant le déplacement. |
2) nous rapprochons les circuits l'un de l'autre, le galvanomètre
détecte un courant de sens contraire pendant le déplacement.
3) changer le sens du courant dans le circuit 1 change dans les expériences
1) et 2) le sens du courant dans le circuit 2.
4) les expériences 1) et 2) peuvent être reprises avec
un aimant à la place du circuit 1 ; le retournement de l'aimant
(inversion des pôles) inverse le sens du courant.
5) à l'aide d'un dispositif, nous faisons varier l'intensité
du courant dans le circuit 1, le galvanomètre détecte un
courant dans le circuit 2 dont le sens dépend du sens de la variation
de l'intensité (augmentation ou diminution).
Les expériences 1), 2), 3) et 4) font état du déplacement
relatif d'un dispositif par rapport à l'autre. Dans l'expérience
5), le phénomène est lié à la variation du
champ magnétique par variation de l'intensité du courant
qui le crée.
En fait, l'expérience 5) n'est pas très différente.
En effet, supposons une augmentation (ou diminution) de l'intensité
du courant du circuit 1, elle produit, au niveau du circuit 2, une augmentation
(ou diminution) de l'intensité du champ magnétique (créé
par le circuit 1) qui provoque (induit) un courant dans le circuit 2.
Dans les autres expériences, un rapprochement (ou éloignement)
entre les circuits provoque une augmentation (ou diminution) de l'intensité
du champ magnétique. La conséquence est identique, il y a
induction d'un courant électrique dans le circuit 2.
Le sens du courant induit n'est pas indifférent. Dans les expériences
où il y a déplacement, le sens du courant est tel que la résultante
des forces de Laplace nées de ce courant s'oppose au déplacement.
Dans l'expérience 5), localement le champ magnétique créé
par le courant induit s'oppose au sens de la variation du champ magnétique
du à la variation de courant du circuit 1.
Ceci traduit la loi de Lenz : les effets du courant
induit s'opposent aux causes qui lui on donné naissance. C'est une loi
de modération, de portée très générale en
Physique.
2.2. Etude théorique quantitative
2.2.1. Le circuit où le courant est induit est mobile
Le référentiel est lié au circuit 1 et nous considérons
les expériences où le circuit 2 est mobile dans le champ
magnétique constant créé par le circuit 1.
Les charges (ions et électrons libres) du circuit 2 sont soumises
à une force de Laplace puisqu'elles sont à vitesse ![]() .
.
En ce qui concerne les ions, fixes dans la structure métallique,
une réaction de la structure s'opposera à la force de Laplace.
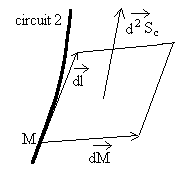 |
Au contraire, les électrons libres, soumis
à la force de Laplace, se déplacent (courant induit Pour les porteurs mobiles au point M, la force de Laplace totale sera 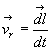 et
et 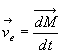 . . |
Le déplacement élémentaire de ces porteurs est ![]() .
.
Le travail élémentaire de la force de Laplace ![]()
En remaniant cette dernière équation, nous obtenons 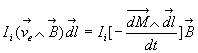
Tout se passe comme s’il apparaissait dans le circuit 2, un champ électromoteur
induit ![]() (donc
une force électromotrice
(donc
une force électromotrice ![]() ).
).
Le déplacement ![]() du circuit 2 a eu pour conséquence sur la charge dq à vitesse
du circuit 2 a eu pour conséquence sur la charge dq à vitesse ![]() ,
la force de Laplace
,
la force de Laplace ![]() qui engendre un mouvement supplémentaire à vitesse
qui engendre un mouvement supplémentaire à vitesse ![]() des
porteurs mobiles du circuit 2.
des
porteurs mobiles du circuit 2.
![]() est un vecteur
dont le module est égal à l'aire engendrée par le déplacement
de l'élément
est un vecteur
dont le module est égal à l'aire engendrée par le déplacement
de l'élément ![]() du
circuit 2.
du
circuit 2.![]() est
le flux du champ magnétique à travers cet élément
de surface. En intégrant à tous les éléments, on
obtient
est
le flux du champ magnétique à travers cet élément
de surface. En intégrant à tous les éléments, on
obtient ![]()
Ainsi il apparaît que la force électromotrice induite ![]() est égale à
est égale à ![]() où
où ![]() est
le flux du champ magnétique à travers la surface engendré
par le déplacement du circuit 2.
est
le flux du champ magnétique à travers la surface engendré
par le déplacement du circuit 2.
Ce flux a été appelé flux coupé ; il est
calculable par deux méthodes (paragraphe 13).
2.2.2. Variation du champ magnétique. Loi de Faraday
Dans le cas de l'expérience 5), la loi expérimentale de Faraday
introduit une force électromotrice induite ![]() où
où ![]() est
le flux du champ magnétique variable à travers une surface quelconque
s'appuyant sur le contour du circuit 2, le champ magnétique variable
se calcule en généralisant la loi de Biot et Savart à des
courants variables (cette généralisation ne pose pas de difficulté
si les temps de propagation sont négligeables).
est
le flux du champ magnétique variable à travers une surface quelconque
s'appuyant sur le contour du circuit 2, le champ magnétique variable
se calcule en généralisant la loi de Biot et Savart à des
courants variables (cette généralisation ne pose pas de difficulté
si les temps de propagation sont négligeables).
Envisager n'importe quelle surface s'appuyant sur le contour du circuit revient
à généraliser à des régimes variables la
conservation du flux du champ magnétique soit ![]()
Cette relation est connue sous le nom d'équation de Maxwell de conservation du flux du champ magnétique.
Rappelons que ![]() ð
ð![]() ,
c'est à dire que le champ magnétique dérive d'un potentiel
vecteur.
,
c'est à dire que le champ magnétique dérive d'un potentiel
vecteur.
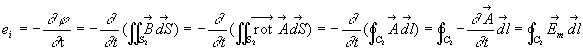
Ainsi, dans le cas de l'expérience 5), la loi de Faraday fait apparaître,
localement, un champ électromoteur 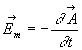 qui met en mouvement à vitesse
qui met en mouvement à vitesse ![]() les
porteurs mobiles par la force
les
porteurs mobiles par la force ![]() .
.
2.2.3. Champ électrique. Equation de Maxwell-Faraday
Les deux causes (champ magnétique variable et déplacement) peuvent
exister en même temps, le champ électromoteur sera 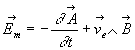 ð
la force électromotrice induite
ð
la force électromotrice induite ![]() .
.
Le signe moins qui apparaît dans l'expression de la force électromotrice induite rappelle la loi de Lenz, le courant induit s'oppose par ses effets à la variation de flux qui lui a donné naissance.
A ce champ électromoteur peut se superposer un champ électrostatique
ou électrocinétique ![]() si
bien que l'action totale sur une charge dq à vitesse
si
bien que l'action totale sur une charge dq à vitesse ![]() sera
sera 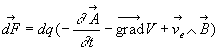 .
.
Le rapprochement de cette dernière expression avec celle de la force
de Laplace conduit à introduire, lorsqu'il y a des variations avec le
temps, un champ électrique 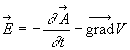 qui conduit à
qui conduit à 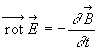
Cette dernière relation très importante est connue sous
le nom d'équation de Maxwell-Faraday.
On appelle dipôle magnétique toute source de magnétisme
quasi-ponctuelle, assimilable à une distribution localisée
de courants dont les dimensions sont très petites devant les distances
où s’exercent ses effets.
Pour un circuit filiforme (C), parcouru par un courant I, on définit
le moment magnétique par ![]() où S est une surface quelconque s’appuyant sur le contour (C),
orientée suivant la " règle du tire-bouchon ".
où S est une surface quelconque s’appuyant sur le contour (C),
orientée suivant la " règle du tire-bouchon ".
Si P est un point du circuit et O un point quelconque, ![]() et
et ![]() .
.
Pour une distribution volumique de courant, on obtient ![]()
3.1.1. Potentiel vecteur et champ magnétique créés
à grande distance
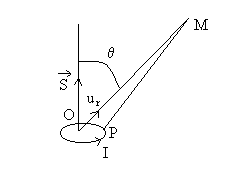 |
O arbitraire est au voisinage du circuit.
Le potentiel vecteur en M éloigné du dipôle est égal à 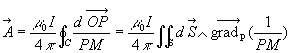
Sur la dimension de S,
|
En coordonnées sphériques, on obtient :
![]() et
et 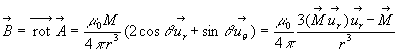
On remarque l’analogie qui peut être faite entre champ électrique
d’un dipôle électrique et champ magnétique d’un dipôle
magnétique (ainsi, il serait possible d’introduire un potentiel scalaire
magnétique 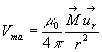 tel que
tel que ![]() ).
).
3.1.2. Action d’un champ magnétique extérieur sur un
dipôle magnétique
L’interaction entre un champ magnétique extérieur ![]() et un circuit électrique se traduit par une énergie potentielle
et un circuit électrique se traduit par une énergie potentielle ![]() où
où ![]() ,
S étant une surface s’appuyant sur le contour du circuit.
,
S étant une surface s’appuyant sur le contour du circuit.
Compte tenu des faible dimensions de ce dernier, ![]() est quasi-uniforme sur S et
est quasi-uniforme sur S et ![]() .
On remarque l’analogie qui peut être faite avec les résultats sur
le dipôle électrique à savoir
.
On remarque l’analogie qui peut être faite avec les résultats sur
le dipôle électrique à savoir ![]()
Dans le champ magnétique extérieur, le dipôle peut avoir
un mouvement de translation (qui correspond au travail de la force résultante ![]() qui
s’exerce sur le dipôle) et un mouvement de rotation (qui correspond au
travail du couple
qui
s’exerce sur le dipôle) et un mouvement de rotation (qui correspond au
travail du couple ![]() qui s’exerce sur le dipôle).
qui s’exerce sur le dipôle).
Par analogie avec le dipôle électrique, on trouve ![]() et
et ![]()
Ces derniers résultats peuvent être démontrés
en calquant la démonstration déjà présentée.
Pour être plus complet, nous présentons une autre démonstration
qui aurait pu être faite dans le cas du dipôle électrique.
Pour un déplacement élémentaire ![]() et une rotation élémentaire
et une rotation élémentaire ![]() ,
on obtient :
,
on obtient :
![]()
En considérant ![]() ,
on peut écrire
,
on peut écrire ![]() .
.
D’autre part, la variation du moment dipolaire due à la rotation est
égale à ![]() .
.
En remplaçant et en réorganisant dans l’expression de ![]() ,
on trouve :
,
on trouve :
![]() et
et ![]()
3.1.3. Magnéton de Bohr
Un électron en rotation sur son orbital est analogue à un circuit
de courant ![]()
Son moment magnétique est ![]()
Le moment cinétique ![]() étant une constante du mouvement dans un mouvement à force centrale,
on obtient :
étant une constante du mouvement dans un mouvement à force centrale,
on obtient :
![]()
La Mécanique quantique introduit une quantification du moment cinétique
où l’intensité du moment cinétique est égal à ![]() .
.
Il apparaît une unité naturelle de moment magnétique appelée
magnéton de Bohr ![]() .
Dans cette formule, l nombre quantique secondaire prend toute valeur
entière telle que
.
Dans cette formule, l nombre quantique secondaire prend toute valeur
entière telle que ![]() où
n est le nombre quantique principal.
où
n est le nombre quantique principal.
Pour un ensemble d’électrons en mouvement autour d’un noyau,
la situation est plus complexe car il s’agit de faire la sommation vectorielle
à tous les éléctrons.
On obtient la relation ![]() où
où ![]() est appelé le rapport gyromagnétique. Dans le cas simple
de l’électron unique, ce rapport est égal à
est appelé le rapport gyromagnétique. Dans le cas simple
de l’électron unique, ce rapport est égal à ![]() .
.
3.1.4. Précession d’un moment magnétique dans un champ
magnétique extérieur uniforme
On applique le théorème du moment cinétique : 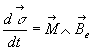 ,
soit
,
soit 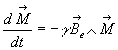 .
.
Cette dernière relation montre que l’intensité du moment magnétique
est constante (![]() )
et que " l’effet d’un champ magnétique sur un moment magnétique
isolé n’est pas d’orienter ce moment dans la direction du champ,
mais de le faire tourner (précesser comme une toupie) autour de la direction
du champ à vitesse angulaire
)
et que " l’effet d’un champ magnétique sur un moment magnétique
isolé n’est pas d’orienter ce moment dans la direction du champ,
mais de le faire tourner (précesser comme une toupie) autour de la direction
du champ à vitesse angulaire ![]() .
.
En Mécanique quantique, on montre que la projection du moment cinétique
orbital sur la direction du champ magnétique est quantifiée et
égale à ![]() où
où ![]() est le nombre quantique magnétique qui prend toute valeur entière
telle que
est le nombre quantique magnétique qui prend toute valeur entière
telle que ![]() .
Dans ces conditions, l’angle
.
Dans ces conditions, l’angle ![]() entre les directions du moment cinétique et le champ magnétique
est défini par
entre les directions du moment cinétique et le champ magnétique
est défini par ![]() .
.
3.2. Aimantation. Excitation magnétique
L’expérience (en particulier celle de Stern et Gerlach) montre qu’il convient d’introduire trois moments magnétiques permanents dans un atome :
Certaines substances possèdent la propriété d'aimantation
induite : si on les dispose dans un champ magnétique elles s'aimantent,
c'est à dire elles acquièrent pour un volume ![]() un dipôle magnétique
un dipôle magnétique ![]() .
.
3.3. Potentiel vecteur créé par une
aimantation. Distribution équivalente de courants
Le vecteur aimantation est défini par 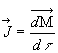
Soient Q un point quelconque du milieu magnétique et
M
un point extérieur à ce milieu.
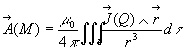 où
où ![]()
Cette formule est d’un emploi simple si le vecteur aimantation est uniforme, on fait l’analogie avec le calcul des champs électrostatiques pour une densité volumique de charge unité.
Dans le cas général, on remarque que 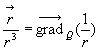 et on utilise la relation d’analyse vectorielle
et on utilise la relation d’analyse vectorielle ![]() .
.
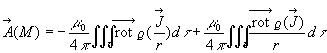
En utilisant la " formule du rotationnel "![]() ,
on obtient
,
on obtient
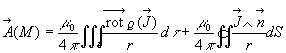 où
où ![]() est le vecteur unitaire normal, en chaque point, à la surface fermée
S, orientée vers l’extérieur.
est le vecteur unitaire normal, en chaque point, à la surface fermée
S, orientée vers l’extérieur.
On constate que le potentiel vecteur créé par l’aimantation est
identique à celui d’une distribution de courants de densité volumique ![]() et de densité surfacique
et de densité surfacique ![]() .
.
En dehors du milieu magnétique, le théorème d’Ampère
est inchangé. Dans le milieu magnétique, il doit être
réécrit en introduisant la distribution équivalente
de courants rendant compte de l’aimantation.
![]() ð
ð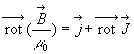
On obtient ![]() où
où 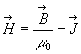 est appelé excitation (champ) magnétique.
est appelé excitation (champ) magnétique.
L'équation ![]() est connue sous le nom de théorème d'Ampère. Son expression
intégrale est
est connue sous le nom de théorème d'Ampère. Son expression
intégrale est ![]() .
.
On conçoit que l'aimantation est d'autant plus forte que le milieu est dense et que le champ extérieur est fort.
Une variation ![]() provoque
une réaction du milieu qui induit un courant qui s'oppose à
cette variation. Pour imposer un champ magnétique dans un milieu,
l'opérateur extérieur devra fournir une énergie qui
sera emmagasinée sous forme d'énergie magnétique.
provoque
une réaction du milieu qui induit un courant qui s'oppose à
cette variation. Pour imposer un champ magnétique dans un milieu,
l'opérateur extérieur devra fournir une énergie qui
sera emmagasinée sous forme d'énergie magnétique.
On admet (sans démonstration) que la densité volumique d'énergie
magnétique emmagasinée pour une variation ![]() est égale à
est égale à ![]()
Si le champ magnétique dans le milieu est égale à ![]() ,
on obtient, après intégration, de la formule précédente
,
on obtient, après intégration, de la formule précédente ![]() .
.
Dans le cas des milieux magnétiques linéaires, on obtient les
formules connues ![]()
4. Conséquences du phénomène d'induction
Les conséquences (ou applications) sont nombreuses. Nous citerons
:
- la transformation énergie mécanique - énergie
électrique c'est à dire la production de courants électriques
continus à partir de dynamos, la production de courants électriques
alternatifs à partir d'alternateurs, les microphones,
- la transformation énergie électrique - énergie
mécanique c'est à dire les moteurs électriques, les
haut-parleurs,
- les circuits électriques comprenant une auto-induction ou
une induction mutuelle,
- les courants de Foucault où le métal peut être
considéré comme formé d'une infinité de petits
circuits dans lesquels prennent naissance des courants induits dits courants
de Foucault.
4.1. Exemple élémentaire de transformation
énergie électrique - énergie mécanique
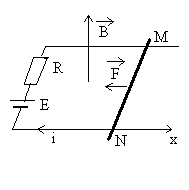 |
Le rail mobile MN , de masse m, de longueur
L, glisse sans frottement sur les rails fixes. Le circuit électrique
ainsi constitué est alimenté par un générateur
de f.e.m. continue E, la résistance R symbolise la
résistance totale du circuit. Le champ magnétique Il se produit des forces de Laplace qui vont provoquer le déplacement du rail mobile et, de ce fait, une force électromotrice induite dans le circuit |
Sur un élément ![]() du rail mobile, la force de Laplace est
du rail mobile, la force de Laplace est ![]() et la résultante
et la résultante ![]() .
.
Le principe fondamental de la dynamique s'écrit : ![]()
La force électromotrice induite est 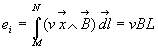 (ce résultat aurait pu être établi à partir du flux
coupé).
(ce résultat aurait pu être établi à partir du flux
coupé).
L'équation électrique est ![]()
Pour trouver le mouvement du rail ou l'intensité électrique,
il convient de découpler les deux équations différentielles
et de les résoudre avec des conditions limites qui peuvent être
: au temps initial, le rail est immobile et on établit le courant.
Nous laissons au lecteur le soin de le faire et nous nous intéressons
au bilan énergétique.
L'équation mécanique donne ![]()
L'équation électrique ![]()
Nous éliminons le terme couplé mécanique-électrique
et on obtient ![]() .
.
En intégrant à partir du temps initial 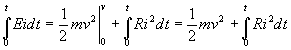
L'énergie électrique fournie par le générateur
est transformée en énergie mécanique et dissipée
par effet joule.
Ce type d'exercice présente toujours des difficultés
de signes ; nous conseillons, avant de faire la résolution des équations
différentielles, de faire le bilan énergétique.
Le lecteur pourra reprendre cet exercice en supprimant le générateur
et en imposant un déplacement au rail MN : il réalisera
un générateur électromécanique.
4.2. Auto-induction. Induction mutuelle
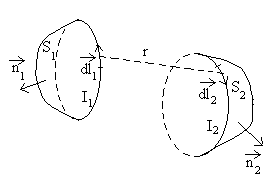 |
On considère deux circuits notés
1 et 2 parcourus par des courants Les deux circuits créent en tout point de l'espace des champs magnétiques notés respectivement |
Le flux de ![]() à travers
à travers ![]() est égal à
est égal à ![]() .
.
Par définition, ![]() est le coefficient d'auto-induction (on dit aussi self-induction ou inductance
propre) du circuit 1.
est le coefficient d'auto-induction (on dit aussi self-induction ou inductance
propre) du circuit 1.
Pareillement, on peut définir le coefficient d'auto-induction du circuit
par la relation ![]() .
.
Le flux de ![]() à travers
à travers ![]() est égal à
est égal à ![]() .
.
![]() est le coefficient
d'induction par influence du circuit 2 du au circuit 1.
est le coefficient
d'induction par influence du circuit 2 du au circuit 1.
Pareillement on peut définir ![]()
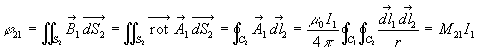
Ainsi, 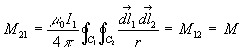
En conséquence, on emploie l'expression coefficient d'influence
mutuelle (inductance mutuelle).
Les formules ci-dessus sont généralisables, sans difficultés
particulières, à des courants surfaciques ou volumiques.
Les signes imposées à l'orientation des surfaces font
que les coefficients d'auto-induction sont positifs, les coefficients d'influence
mutuelle sont positifs ou négatifs.
4.3. Retour sur l'énergie magnétique
On se propose de calculer l'énergie magnétique d'un circuit
parcouru par un courant I. A l'application des formules du paragraphe
35, nous préférons le raisonnement ci-après.
Un générateur a établi le courant qui est passé
de la valeur initiale nulle à la valeur finale I. A un instant
t le courant est i, à un instant ![]() le
courant est
le
courant est ![]() .
.
Une force électromotrice induite ![]() s'oppose à cette variation, le générateur doit fournir
une énergie qui est emmagasinée sous forme magnétique.
s'oppose à cette variation, le générateur doit fournir
une énergie qui est emmagasinée sous forme magnétique.
![]()
Par intégration, on obtient ![]()
Le lecteur, sur l'exercice simple du solénoïde, pourra
vérifier la concordance entre ces formules et celles générales
du paragraphe 35.
Cas de deux circuits
On envisage deux circuits parcourus par des courants établis ![]() ,
par simplification d'écriture nous prenons
,
par simplification d'écriture nous prenons ![]() .
.
![]()
Par intégration ![]()
L'énergie magnétique est positive (emmagasinée) quelques
soient ![]() , ceci
entraîne
, ceci
entraîne ![]() .
.
Ce résultat peut être établi à partir des lignes
de champ magnétique. En effet les lignes de champ, créé
par le circuit 1 et le traversant, ne traversent pas toutes le circuit 2 ð![]()
De même ![]() et par conséquence
et par conséquence ![]() .
.
Les résultats ci-dessus sont généralisables à un nombre quelconque de circuits.