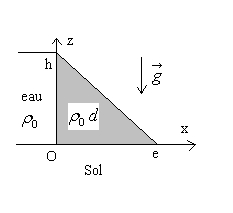Exercices de statique des fluides
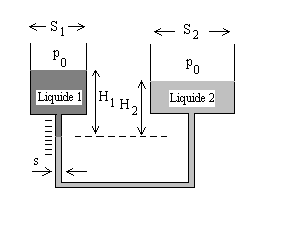
1 - La figure schématise un manomètre
à liquide (masse volumique m) à
réservoir de section
3) On incline le tube du manomètre, sa direction
faisant un angle a avec le plan horizontal.
La position du ménisque le long du tube est repérée par
son abscisse Z.
Calculer la nouvelle sensibilité.
Réponse
1 | Réponse
2 | Réponse
3 |
2 - Un manomètre différentiel est constitué
de deux récipients cylindriques, de sections droites respectives  ,
reliés par un tube de section intérieure s constante.
,
reliés par un tube de section intérieure s constante.
A.N. 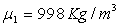 ;
; 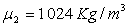 ;
; 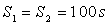
Réponse
1 | Réponse
2 |
|
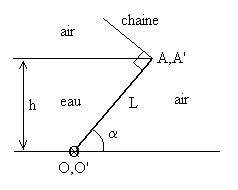
3 – La figure ci-contre représente une
vanne rectan-gulaire (L x l) en coupe verticale destinée
à fixer le niveau d’eau (hauteur h) d’une retenue. Cette
vanne est articulée à sa base sur un axe OO’ et maintenue
au sommet par 2 chaînes parallèles manoeuvrées par
un treuil. En position haute (angle a) on supposera
la direction des chaînes perpendiculaires à la vanne.
1) Calculer la poussée sur la vanne due à la pression
hydrostatique et son centre d’application.
|
|
2) Calculer les efforts transmis aux chaînes (on
négligera le poids propre de la vanne) et la réaction de l’axe
OO’.
Application numérique : h = 4m
; L = 5m ; l = 6m
Réponse
1 | Réponse
2 |
4 - On remplit d’eau sur une hauteur h un verre de forme cylindrique.
On appelle S la section de sa base.
1) Calculer la résultante des forces de pression sur les parois du verre.
Interpréter le résultat
2) Mêmes questions avec un verre en forme de cône, un verre ballon.
Réponse
1 | Réponse
2 |
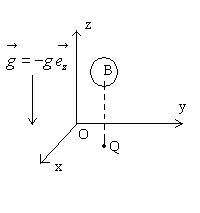
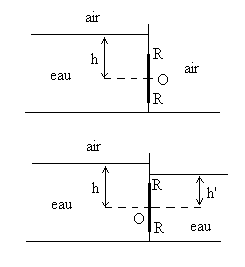
| 5 - Une vanne de vidange est constituée
par un disque de rayon R pivotant autour d’un axe horizontal. Le
centre O du disque est positionné à une hauteur h par
rapport au niveau d’eau.
1) Calculer la poussée sur le disque et la position
du centre de poussée.
2) Reprendre le calcul dans le cas où le disque
est noyé (eau de chaque coté du disque). Ce cas est celui
d’une écluse.
Application numérique : h = 2m
; R = 0,5m
|
|
Réponse
1 | Réponse
2 |
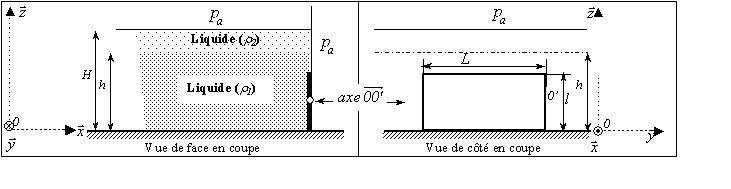
6) Une vanne plane verticale de forme rectangulaire
(largeur L et de hauteur l), articulée autour d’un axe
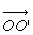 (figure ci-dessous),
maintient le niveau de deux liquides non miscibles de masses volumiques respectives
(figure ci-dessous),
maintient le niveau de deux liquides non miscibles de masses volumiques respectives
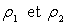 . Le niveau
du liquide de masse volumique
. Le niveau
du liquide de masse volumique 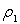 se situe à une hauteur h (le liquide 1 dépasse l’extrémité
haute de la vanne). L’autre liquide de masse volumique
se situe à une hauteur h (le liquide 1 dépasse l’extrémité
haute de la vanne). L’autre liquide de masse volumique 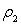 est situé à une hauteur H-h au de dessus du premier liquide.
La face de la vanne du côté liquide est complètement noyée
dans le liquide de masse volumique
est situé à une hauteur H-h au de dessus du premier liquide.
La face de la vanne du côté liquide est complètement noyée
dans le liquide de masse volumique 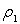 .
.
1) Calculer la force de poussée due à la pression hydrostatique
du liquide s’exerçant sur la face verticale de la vanne.
2) Déterminer la position du point d’application C de cette
poussée en fonction de 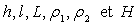 .
.
On vérifiera que 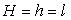 ð
ð 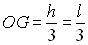
Réponse
1 | Réponse
2 |
|
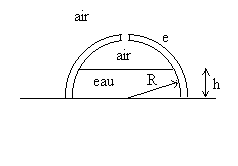
7 - Une cloche hémisphèrique ( rayon
R, épaisseur
e<< R, masse m) repose sur un plan horizontal.
Elle contient de l’eau jusqu’à une hauteur h. Un orifice
pratiqué au sommet permet de maintenir la pression atmosphèrique
à l’interface eau/air.
L’épaisseur de paroi e est suffisamment faible pour considérer
comme identiques les surfaces intérieure et extérieure de
la cloche.
Montrer qu’il existe une hauteur critique 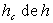 au
delà de laquelle l’équilibre est rompu (la cloche se soulève) au
delà de laquelle l’équilibre est rompu (la cloche se soulève)
|
|
Application numérique : cloche en verre de densité
d = 2,5 telle que e/R = 0,02
Réponse
1 |
|
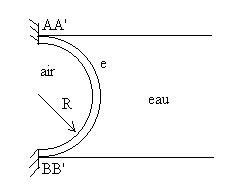
8 - Etude succincte d’un barrage voûte en
forme de ½ cylindre (épaisseur de paroi e, rayon moyen R,
hauteur h ; e/R << 1).
Ce barrage est en appui selon AA’ et BB’ (parallèle à l’axe
z vertical de la voûte).
Calculer la poussée totale sur le barrage et la
réaction des appuis.
Application numérique : h = R = 100m ; e
= 10m
|
|
Réponse
1 |
9 – Un récipient cylindrique de rayon 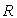 ,
d’axe vertical
,
d’axe vertical 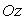 ,
contient une hauteur
,
contient une hauteur 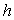 de liquide de masse volumique
de liquide de masse volumique 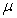 .
Le récipient est mis en rotation, à vitesse angulaire
.
Le récipient est mis en rotation, à vitesse angulaire 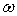 ,
autour de l’axe
,
autour de l’axe 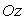 .
.
Le liquide est entraîné par le cylindre et on admet que chaque
couche de liquide est entraînée à la vitesse angulaire.
Dans un référentiel tournant à la vitesse angulaire 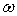 ,
le liquide est donc en équilibre dans le référentiel tournant.
,
le liquide est donc en équilibre dans le référentiel tournant.
On se propose de déterminer la forme de la surface libre du liquide.
Réponse
1 |
10 - Démontrer la loi de Laplace pour un goutte sphérique
de liquide dans de l’air, pour une bulle de vapeur dans un liquide, pour une
bulle de savon.
Réponse
1 | Réponse
2 |
11 – Démontrer la loi de Jurin
Réponse
1 |
12 – Formation d’un courant ascendant (Capes externe 1991)
Dans toute l’étude qui suit, le champ de pesanteur est
supposé uniforme, l’air se comporte comme un gaz parfait de masse molaire
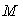 et de capacités
thermiques
et de capacités
thermiques 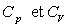 constantes.
constantes.
L’air est supposé sec. Un point N de l’atmosphère est repéré
par ses coordonnées cartésiennes dans un trièdre orthonormé
(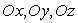 ), tel que l’axe
), tel que l’axe
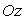 coïncide
avec la verticale ascendante, la cote
coïncide
avec la verticale ascendante, la cote 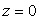 étant prise au niveau de la mer. Le module de l’accélération
de la pesanteur est appelé
étant prise au niveau de la mer. Le module de l’accélération
de la pesanteur est appelé 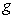 .
On désigne par
.
On désigne par 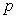 la pression au point
la pression au point 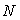 .
.
1) L’air est supposé être un fluide de
masse volumique 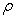 localement en état d’équilibre. On considère une tranche
d’air d’épaisseur
localement en état d’équilibre. On considère une tranche
d’air d’épaisseur 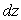 ,
de volume
,
de volume 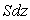 . Préciser,
à l’aide d’un schéma, la nature et la direction des forces extérieures
appliquées sur cette tranche.
. Préciser,
à l’aide d’un schéma, la nature et la direction des forces extérieures
appliquées sur cette tranche.
En écrivant que cette tranche reste en équilibre, établir
la relation : 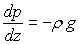
On appelle 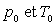 la pression et la température thermodynamique au niveau de la mer,
la pression et la température thermodynamique au niveau de la mer,  la pression et la température thermodynamique à la cote
la pression et la température thermodynamique à la cote 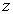 .
Exprimer
.
Exprimer 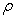 à l’altitude
à l’altitude 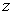 en fonction de
en fonction de 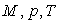 et de la constante molaire des gaz parfaits
et de la constante molaire des gaz parfaits 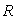 .
.
Des relevés expérimentaux montrent qu’en l’absence de mouvement
des masses d’air, la température est fonction affine de l’altitude 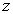 ,
pour
,
pour 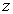 variant
de
variant
de 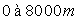 , suivant
la loi :
, suivant
la loi :  .
.
A l’aide de l’équation d’état des gaz parfaits et des relations
précédentes, montrer que la pression 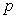 et la température
et la température 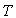 à l’altitude
à l’altitude 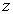 sont liées par la relation, appelée " loi de nivellement
barométrique " :
sont liées par la relation, appelée " loi de nivellement
barométrique " : 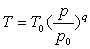 où l’on exprimera l’exposant
où l’on exprimera l’exposant 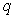 en fonction de
en fonction de 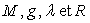 . Quelle est la
dimension physique de cet exposant ? Calculer numériquement
. Quelle est la
dimension physique de cet exposant ? Calculer numériquement 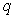 sachant que
sachant que 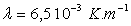 .
.
On donne : 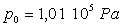 et
et 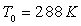 . Exprimer
numériquement la pression
. Exprimer
numériquement la pression 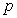 en fonction de la température
en fonction de la température 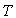 .
.
2) L’état d’équilibre étudié
précédemment n’est possible que si les isothermes et les isobares
coïncident avec les équipotentielles du champ de pesanteur, donc
ici avec les surfaces d’équation 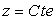 .
Si, par suite d’hétérogénéités du sol, celui-ci
présente des écarts de température d’un point à
un autre, l’air qui surmonte ces terrains s’échauffe différemment
et se met en mouvement. On se propose d’étudier de façon très
simplifiée la formation d’un courant ascendant.
.
Si, par suite d’hétérogénéités du sol, celui-ci
présente des écarts de température d’un point à
un autre, l’air qui surmonte ces terrains s’échauffe différemment
et se met en mouvement. On se propose d’étudier de façon très
simplifiée la formation d’un courant ascendant.
Réponse
1 | Réponse
2 |
13) Etude d’un barrage-poids
|
Le barrage-poids est représenté en coupe
sur la figure ci-contre, la longueur suivant la direction y sera
prise unitaire.
Le matériau constituant le barrage a pour masse volumique 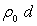 où
où 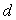 est la densité du matériau par rapport à l’eau de
masse volumique
est la densité du matériau par rapport à l’eau de
masse volumique 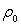 . .
La composante verticale de la force exercée par
le sol sur le barrage est de la forme : 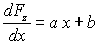
|
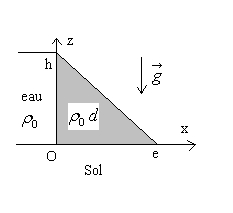
|
- En exprimant les conditions d’équilibre du barrage, calculer les
valeurs de
 en fonction de
en fonction de 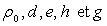
- Pourquoi convient-il que
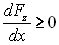 ?
En déduire une condition entre
?
En déduire une condition entre 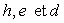
- Quelle doit être la valeur de la composante horizontale exercée
par le sol sur le barrage.
Réponse
1 |
![]() ,
on a
,
on a ![]() repérable
à travers le tube. Lorsque
repérable
à travers le tube. Lorsque ![]() ,
les cotes des deux surfaces libres deviennent
,
les cotes des deux surfaces libres deviennent ![]() et z, cette dernière cote étant seule repérable.
et z, cette dernière cote étant seule repérable.![]() en fonction de (
en fonction de (![]() )
et de m, g, s, S
(
)
et de m, g, s, S
(![]() ).
).![]()