Exercices de mécanique du solide
1) Chute d’une tige sur le sol
|
|
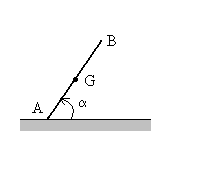
Une tige AB, homogène, de centre G
et de longueur 2b, est posée sur le sol horizontal, verticalement
sans vitesse initiale. Sous l’action d’un léger déséquilibre,
elle tombe.
En supposant que l’extrémité A glisse sans frottement
sur le sol, calculer la vitesse 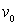 du centre G de la tige quand celle-ci heurte le sol.
du centre G de la tige quand celle-ci heurte le sol.
On pourra démontrer la valeur du moment d’inertie de la tige
par rapport à sa médiatrice 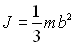
|
| Réponse
|
2) Mouvement d’une barre appuyée contre un mur
|
|
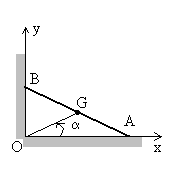
Le référentiel terrestre est supposé
galiléen. Une barre AB, homogène, de masse m,
de longueur 2b et de centre G, milieu de AB, est
posée sur le sol horizontal et repose contre un mur vertical. Sa
position est déterminée par l’angle 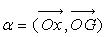 . .
Les contacts en A et en B sont supposés sans frottement.
a) Ecrire l’intégrale première du mouvement en supposant,
qu’à l’instant initial, la barre est immobile avec une inclinaison
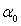 . .
|
b) Calculer la réaction 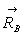 du mur sur la barre et en déduire pour quelle inclinaison
du mur sur la barre et en déduire pour quelle inclinaison 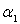 la barre quitte le mur.
la barre quitte le mur.
On pourra démontrer la valeur du moment d’inertie
de la tige par rapport à sa médiatrice 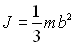
| Réponse
a | Réponse
b |
3) Mouvement d’une barre sur un axe horizontal
|
|
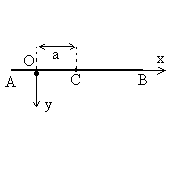
(Oxyz) est un référentiel galiléen.
Une barre homogène AB, de masse m, de longueur 2b,
de centre C, de moment d’inertie 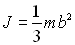 par rapport à un axe passant par C et perpendiculaire à
la barre, est posée sur une tige de rayon négligeable, coïncidant
avec l’axe Oz. Le contact entre la barre et la tige est caractérisé
par un coefficient de frottement f. A l’instant initial, on lâche
la barre sans vitesse initiale dans la position horizontale (
par rapport à un axe passant par C et perpendiculaire à
la barre, est posée sur une tige de rayon négligeable, coïncidant
avec l’axe Oz. Le contact entre la barre et la tige est caractérisé
par un coefficient de frottement f. A l’instant initial, on lâche
la barre sans vitesse initiale dans la position horizontale (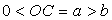 ) )
|
Pour quelle inclinaison 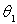 la barre commence t’elle à glisser sur la tige ?
la barre commence t’elle à glisser sur la tige ?
| Réponse |
4) Mouvement d’un chasse-neige
|
|
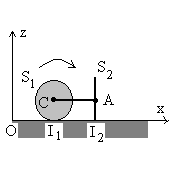
La figure schématise un chasse-neige se déplaçant
sur une horizontale.
Ce chasse-neige est constitué d’une roue S1
(de centre d’inertie C, de rayon R, de masse m répartie
uniformément sur la circonférence et de moment d’inertie
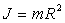 par rapport
à son axe) et d’une partie S2 (CABI2
), indéformable de même masse m que la roue, de centre
d’inertie A (on donne : par rapport
à son axe) et d’une partie S2 (CABI2
), indéformable de même masse m que la roue, de centre
d’inertie A (on donne : 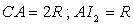 ),
en mouvement de translation parallèlement à l’axe Ox. ),
en mouvement de translation parallèlement à l’axe Ox.
|
Le moteur exerce sur la roue un couple de moment 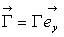 (G constante positive).
(G constante positive).
La roue tourne sans frottement autour de son axe et roule sans glisser sur le
sol. On suppose que le coefficient de frottement de glissement f sur le
sol est le même en I1 et en I2
(il vérifie 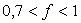 ).
).
a) Appliquer :
- à l’ensemble, le théorème de la résultante dynamique,
- à l’ensemble, le théorème du moment cinétique
au centre de masse du chasse-neige,
- à la roue, le théorème du moment cinétique en
C.
b) Ecrire les relations imposées par le roulement
sans glissement en 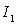 et le glissement en
et le glissement en 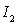 .
.
c) Quelles conditions doit vérifier le moment
G pour que le mouvement déterminé ci-dessus
soit effectivement réalisé ? On pourra supposer qu’à
l’instant initial le chasse-neige est fixe.
| Réponse
a | Réponse
b | Réponse
c |
5) Mouvement d’un cylindre sur un plan incliné
|
|
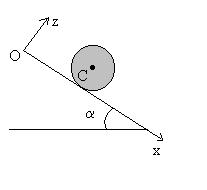
Un cylindre homogène, de centre d’inertie C,
de rayon R et de moment d’inertie (que l’on démontrera)
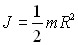 par rapport
à son axe, est posé sans vitesse initiale sur un plan incliné
d’un angle a sur l’horizontale, dans
le référentiel terrestre supposé galiléen. par rapport
à son axe, est posé sans vitesse initiale sur un plan incliné
d’un angle a sur l’horizontale, dans
le référentiel terrestre supposé galiléen.
On désigne par f le coefficient de frottement de glissement
entre le cylindre et le plan incliné.
|
a) Déterminer l’accélération 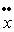 du cylindre. Montrer qu’il y a glissement ou non selon la valeur a
.
du cylindre. Montrer qu’il y a glissement ou non selon la valeur a
.
b) Faire un bilan énergétique entre les
instants 0 et t. Etudier le cas du mouvement sans glissement et celui
avec glissement.
| Réponse
a | Réponse
b |
6) Mouvement d’un point matériel dans un tuyau qui
roule sans glisser
|
|
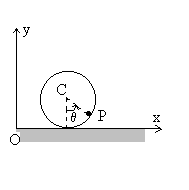
Dans le référentiel terrestre supposé
galiléen, un tuyau cylindrique de rayon R , de masse M,
de moment d’inertie 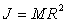 par rapport à son axe, roule sans glisser sur le sol horizontal.
par rapport à son axe, roule sans glisser sur le sol horizontal.
a) A l’intérieur de ce tuyau glisse sans frottement, dans
le plan vertical, un point matériel P de masse m.
L’ensemble est repéré par l’abscisse x du centre
C du tuyau et par l’angle 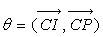 définissant la position du point matériel P.
définissant la position du point matériel P.
|
A l’instant initial, l’ensemble est immobile et 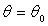 .
.
Ecrire deux équations vérifiées par 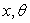 et leurs dérivées.
et leurs dérivées.
En supposant 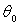 petit,
calculer la période des petites oscillations du système.
petit,
calculer la période des petites oscillations du système.
b) Le point matériel P de masse m
est maintenant solidaire du tuyau.
Calculer la période dans le cas de petites oscillations.
| Réponse
a | Réponse
b |
7) Oscillations d’un demi-disque sur un plan horizontal
|

|
On considère un demi-disque (D) homogène,
de " centre " C, de centre de masse G,
de rayon R et de masse m.
Le référentiel terrestre (Oxyz) est supposé
galiléen.
Tout en restant dans le plan vertical (Oxy), le demi-disque roule
sans glisser sur le plan horizontal.
On désigne par I le point de contact entre le sol et (D).et
on repère la position de (D) par l’abscisse x de C
et par l’angle 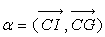 .
A l’instant initial, on lâche (D) sans vitesse initiale dans la
position .
A l’instant initial, on lâche (D) sans vitesse initiale dans la
position 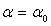 . .
|
On démontrera que 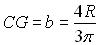 .
.
Le moment d’inertie de (D) par rapport à un axe passant par C
perpendiculaire à (D) vaut 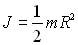 .
.
a) Ecrire une intégrale première du mouvement.
b) En déduire la période des petites oscillations.
| Réponse
a | Réponse
b |
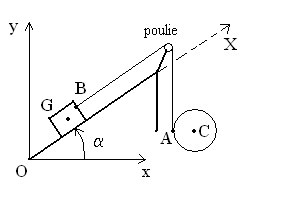
8) Entraînement d'un cube par un cylindre
Le cube glisse sans frottements sur le plan incliné
et on considère que la poulie a une masse négligeable et tourne
sans frottements autour de son axe de rotation.
Le système est abandonné sans vitesse initiale, le fil n'étant
ni lâché, ni tendu, le brin entre la poulie et le cylindre étant
parfaitement vertical et celui entre la poulie et le cube parallèle au
plan incliné. On note 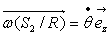 .
.
1) Appliquer le théorème de la résultante
dynamique au cylindre. En déduire que le mouvement de C est vertical.
2) Appliquer le théorème du moment dynamique
au cylindre par rapport à C.
3) Sachant que la poulie roule sans glisser sur le fil
en A, trouver une relation entre l'intensité vitesse 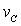 du centre C, l'intensité de la vitesse de translation
du centre C, l'intensité de la vitesse de translation 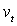 du cube, a et
du cube, a et 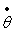 .
.
4) Appliquer le théorème de la résultante
dynamique au cube.
5) En déduire les accélérations
de G et C. Discuter suivant les valeurs de a
.
| Réponse
1 | Réponse
2 | Réponse
3 | Réponse
4 | Réponse
5 |
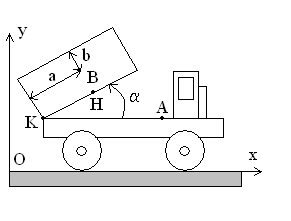
9) Déplacement d'un camion sur un sol horizontal
|
Dans le référentiel terrestre supposé
galiléen, le chauffeur d'un camion (tracteur+benne) immobile sur
une route horizontale a coupé le moteur, mais oublié de
serrer ses freins. Il fait alors basculer la benne d'un angle a
à un angle 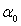 .
La masse du tracteur est notée M, celle de la benne est
notée m. On note A le centre de masse du tracteur,
B celui de la benne et G celui du camion. .
La masse du tracteur est notée M, celle de la benne est
notée m. On note A le centre de masse du tracteur,
B celui de la benne et G celui du camion.
Le camion est posée sur ses 4 roues, chacune de centre 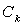 et de masse négligeable, tournant autour sans frottements autour
de leur axe respectif.
et de masse négligeable, tournant autour sans frottements autour
de leur axe respectif.
|
|
On note 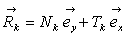 les réactions
du sol sur la roue au niveau de chacun des points de contact camion-sol.
les réactions
du sol sur la roue au niveau de chacun des points de contact camion-sol.
1) Appliquer le théorème du moment dynamique
à une roue et en déduire la direction des forces de contact entre
le camion et le sol.
2) Appliquer le théorème de la résultante
dynamique au camion entier. Qu'en déduisez vous pour le centre de masse
G du camion.
3) En déduire le déplacement horizontal
d du centre de masse A du tracteur
| Réponse
1 | Réponse
2 | Réponse
3 |

![]() du centre G de la tige quand celle-ci heurte le sol.
du centre G de la tige quand celle-ci heurte le sol.![]()