Exercices sur les champs de forces

Champs d’attraction universelle

Problème

1) On admet que la Terre présente une distribution volumique de masse à symétrie sphérique de centre O. Soit R le rayon terrestre et G(R) l’intensité du champ d’attraction universelle au niveau de la mer.
1)1) Calculer la masse volumique moyenne de la Terre.

A.N.  ;  ;

| Réponse 11 |

1)2) On admet maintenant que où r représente la distance au centre O et où sont des constantes positives.
Calculer le champ d’attraction universelle et le potentiel V(r) en tout point de l’espace.
Etablir une relation entre . Calculer si . Représenter G(r). Conclusion.

| Réponse 12 |

Pour la suite du problème, on pourra utiliser .

2) Effet de plateau
2)1) Déterminer en tout point de l’espace le champ d’attraction universelle d’un plateau homogène de masse volumique , d’épaisseur e, dont les dimensions latérales, très grandes devant e, peuvent être considérées comme infinies.

| Réponse 21 |

2)2) Le plateau est en contact avec la Terre modélisée en 1).
Déterminer le champ d’attraction universelle , en déduire la correction de plateau (correction de Bouguer) définie par 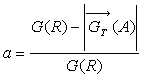en fonction de .
Que devient a pour  ?
A.N. Calculer a pour et .

| Réponse 22 |

3) Prospection gravimétrique. Anomalie de Bouguer .

Il s’agit d’étudier l’effet d’une modification locale de la masse volumique près de la surface de la Terre et la possibilité de la détecter en utilisant les gravimètres modernes dont la limite de détection est de l’ordre du microgal ()

| Réponse 31 |

3)2) Localement, la surface de la Terre peut être considérée comme plane et le champ d’attraction universelle terrestre uniforme.
Soit la masse volumique constante du terrain homogène dans la zone considérée. Un amas sphérique homogène de centre A, de rayon R’, de masse volumique est enfoui à la distance de la surface du sol.

- en utilisant le résultat du 3)1) et en remarquant que a(N) est approximativement la projection de sur la normale au plan (P), montrer que la connaissance de cette anomalie en tout point N du plan (P) permet de déterminer la masse perturbatrice M’ sans connaître L.
- Déterminer l’anomalie de Bouguer dans le cas d’une cavité sphérique creuse. On considère une cavité sphérique de située dans un terrain de masse volumique dont le centre est situé à 10 m de la surface du sol. Déterminer a(N) en H et en N tel que . Cette anomalie est-elle mesurable ?

| Réponse 32 |

1) Un segment, de milieu O, de direction x, est porteur d’une densité linéaire de charges uniforme . Calculer le champ et le potentiel en tout point de l’axe Ox et en tout point de l’axe Oy directement perpendiculaire.

| Réponse 1 |

2) La demi-droite Ay porte une densité linéique de charges uniforme l .
Déterminer le champ en M (

| Réponse 2 |

3a) Calculer le champ et le potentiel électrostatiques créés en tout point de l’espace par un plan uniformément chargé en surface d’une densité . Représenter champ et potentiel.
3)b) Calculer le champ et le potentiel électrostatiques créés en tout point de l’espace par une distribution volumique de charges uniforme de densité située entre deux plans parallèles distants de 2e. Cas limite où .

| Réponse 3a | Réponse 3b |

4)a) Soit un disque de rayon R d’épaisseur négligeable portant une densité surfacique de charges uniforme .
Calculer le champ et le potentiel électrostatiques en tout point de l’axe du disque. Retrouver le résultat du plan uniformément chargé.
4)b) On considère une couronne circulaire de centre O, de rayons R et R’ (R<R’). Cette couronne porte une densité surfacique de charges uniforme s .
Calculer le champ et le potentiel en un point de l’axe de la couronne. Examiner les cas particuliers.

| Réponse 4a | Réponse 4b |

5)a) Calculer le champ et le potentiel créés en un point à distance r d’une ligne infinie portant une densité linéique de charges l uniforme.
Déterminer, dans le cas de deux lignes infinies parallèles distantes de 2e portant des densités linéiques de charges uniformes , les surfaces équipotentielles.
5)b) Soit un cylindre de longueur infinie, de rayon R , portant une densité surfacique s uniforme. Déterminer le champ et le potentiel en tout point.
5)c) Calculer le champ et le potentiel créés en tout point par un cylindre de longueur infinie, de rayon R, portant une densité volumique de charges r uniforme.

| Réponse 5a | Réponse 5b | Réponse 5c |

6)a) On considère une sphère de centre O de rayon R portant une densité surfacique de charges s uniforme. Calculer le champ et le potentiel en tout point.
6)b) On considère une sphère de centre O de rayon R portant une densité volumique de charges r uniforme. Calculer le champ et le potentiel en tout point.
6)c) On considère une distribution de charges à symétrie sphérique centrée en O telle qu’ à une distance x de O, . Calculer le champ en tout point.

| Réponse 6a | Réponse 6b | Réponse 6c |

7) Un système de charges crée en tout point M de l’espace un potentiel V(M) tel que :
où r est la distance de M à une origine fixe O.
La charge q est positive.
On se propose de déterminer complètement le système de charges et d’en donner une signification physique.

Pour cela, on déterminera,
- la valeur asymptotique de la fonction V(M) quand ,
- la valeur de V(M) quand ,
- la densité volumique de charges .

| Réponse 7 |