Oscillateurs à un degré de liberté
Exercices
1 - Une masse m est reliée à deux
ressorts identiques placés verticalement. Les extrémités
des ressorts sont distants de 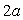 .
Chaque ressort non tendu a une longueur
.
Chaque ressort non tendu a une longueur 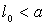 ,
sa raideur est k.
,
sa raideur est k.
1)1) Calculer, à l’équilibre, les longueurs  des ressorts. Montrer que, si
des ressorts. Montrer que, si 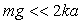 ,
on peut prendre
,
on peut prendre 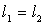 .
.
1)2) Dans cette hypothèse, la masse m peut se déplacer
horizontalement de x à partir de sa position d’équilibre.
Etablir l’équation du mouvement. Résoudre cette équation
en supposant 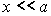 . Trouver
une intégrale première du mouvement et une constante du mouvement.
. Trouver
une intégrale première du mouvement et une constante du mouvement.
| Réponse
11 | Réponse
12 |
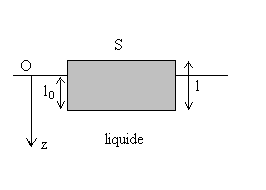
2 - Un solide homogène de section S ,
de hauteur l, de masse volumique 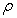 flotte sur un liquide de masse volumique
flotte sur un liquide de masse volumique 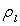 .
.
2)3) Trouver une intégrale première du
mouvement et une constante du mouvement.
On négligera toute force de frottement du liquide sur le solide.
| Réponse
21 | Réponse
22 | Réponse
23 |
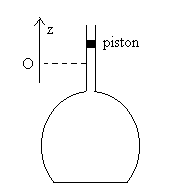
3 - On considère un récipient fermé
par un piston de masse 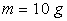 mobile sans frottements
mobile sans frottements
3)2)1) Décrire la nature des mouvements (de faible amplitude)
du piston.
3)2)2) Soit z la position du piston par rapport à sa position
d’équilibre. Ecrire la variation de volume 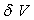 du gaz intérieur.
du gaz intérieur.
3)2)3) Trouver une relation entre les variations de volume 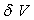 et
et 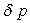 du gaz intérieur
(ces variations restent faibles devant respectivement V et
du gaz intérieur
(ces variations restent faibles devant respectivement V et 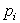 ).
).
3)2)4) En déduire l’équation différentielle du mouvement
du piston. Donner l’expression théorique de la période 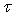 du mouvement. Si
du mouvement. Si 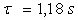 est la période, calculer g .
est la période, calculer g .
3)2)5) Trouver une intégrale première du mouvement et une
constante du mouvement.
| Réponse
31 | Réponse
321 | Réponse
322 | Réponse
323 | Réponse
324 | Réponse
325 |
Problème
A) Régime transitoire d’un oscillateur
mécanique
|
|
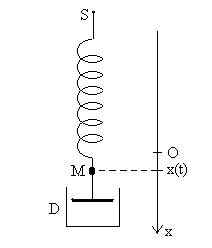
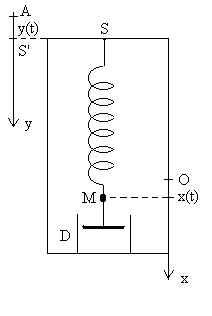
Un ressort élastique, de masse négligeable,
de raideur 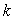 ,
de longueur à vide ,
de longueur à vide  ,
a son extrémité supérieure S fixe. A l’extrémité
inférieure est fixé un corps M assimilable à un point
matériel de masse ,
a son extrémité supérieure S fixe. A l’extrémité
inférieure est fixé un corps M assimilable à un point
matériel de masse 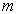 . .
Le rôle unique de l’amortisseur D, de masse négligeable,
lié à M, est d’exercer sur le corps la force 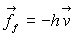 ,
où ,
où 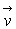 désigne
la vitesse de M et désigne
la vitesse de M et 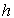 un coefficient de frottement fluide, positif.
un coefficient de frottement fluide, positif.
Les mouvements de M sont verticaux; ils sont étudiés dans
le référentiel, considéré comme galiléen,
pour lequel S est fixe.
La position M est repérée, au cours du temps, par son abscisse
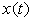 sur l’axe
vertical descendant sur l’axe
vertical descendant 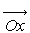 ,
fixe. A l’équilibre, l’abscisse de M est nulle. ,
fixe. A l’équilibre, l’abscisse de M est nulle.
|
A)1) Expliquer la phrase " référentiel
considéré comme galiléen ".
A)2) A l’équilibre, l’allongement du ressort est désigné
par 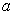 . Exprimer
. Exprimer 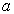 en fonction de
en fonction de  ,
de
,
de 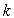 et de la valeur
absolue
et de la valeur
absolue 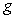 de l’intensité
de pesanteur.
de l’intensité
de pesanteur.
A)3) Etablir l’équation différentielle du mouvement de
M.
A)4) On supprime l’amortisseur D, puis on abandonne M sans vitesse initiale
à l’abscisse 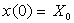 .
Etablir l’expression de
.
Etablir l’expression de 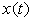 ;
on posera
;
on posera  .
.
Calculer l'énergie cinétique, l'énergie potentielle et
l'énergie mécanique à un instant t.
Calculer les valeurs moyennes des énergies cinétique et potentielle.
Conclusion.
A)5) Après avoir replacé l’amortisseur D, on reprend la
même opération que celle décrite précédemment
en A)4), on posera 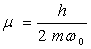 .
.
Dire qualitativement quels sont les régimes possibles d’évolution
de 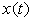 . La résolution de l’équation
différentielle n’est pas demandée.
. La résolution de l’équation
différentielle n’est pas demandée.
Définir et exprimer le coefficient de frottement critique  .
.
A)6) Calculer l’énergie dissipée dans
l’amortisseur D pendant le régime transitoire.
| Réponse
A1 | Réponse
A2 | Réponse
A3 | Réponse
A4 | Réponse
A5 | Réponse
A6 |
B) Oscillations forcées d’un oscillateur
mécanique
Au dispositif de la partie A, on ajoute un dispositif supplémentaire
grâce auquel le corps M est soumis à la force verticale 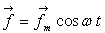 ,
qui vient s’ajouter aux forces étudiées dans la partie A.
,
qui vient s’ajouter aux forces étudiées dans la partie A.
B)1) Etablir l’équation différentielle
du mouvement de M.
B)2) Calculer l’amplitude 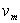 de la vitesse.
de la vitesse.
Définir puis établir l'expression donnant la bande passante.
Définir puis établir l'expression donnant le facteur de qualité
Q.
Calculer le déphasage 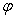 entre
la vitesse et la force.
entre
la vitesse et la force.
B)3) Calculer, en régime forcé, pour 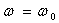 :
:
B)3)a) l’énergie 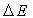 dissipée en une période ;
dissipée en une période ;
B)3)b) l’énergie cinétique maximale 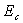 ;
;
B)3)c) l’énergie potentielle maximale 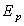 (l’énergie potentielle de référence sera prise en
(l’énergie potentielle de référence sera prise en 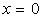 )
)
B)3)d) l’expression  ;
conclusion.
;
conclusion.
| Réponse
B1 | Réponse
B2 | Réponse
B3a | Réponse
B3b | Réponse
B3c | Réponse
B3d |
C) Principe d’un sismographe
C)2) En régime forcé, 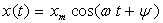 .
On pose
.
On pose 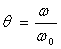 et
et 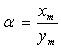 .
.
C)2)a) Exprimer 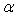 en
fonction de
en
fonction de 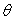 et
de
et
de 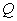 .
.
C)2)b) Exprimer 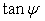 en fonction de
en fonction de 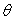 et de
et de 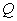 .
.
C)3) Le conditions d’utilisation du sismographe sont telles que  doit être égal à
doit être égal à 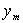 ,
à 2 % près, pour
,
à 2 % près, pour 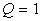 .
Déterminer le domaine de variation de
.
Déterminer le domaine de variation de 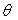 .
.
| Réponse
C1 | Réponse
C2a | Réponse
C2b | Réponse
C3 |
D) Vibration d'une molécule
La molécule d'HCl peut être schématisée par
deux points matériels 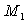 et
et 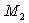 , de masses
respectives
, de masses
respectives 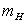 et
et
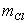 , portant des charges
respectives
, portant des charges
respectives 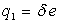 et
et
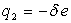 .
.
On pose 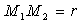 et on
donne les valeurs numériques suivantes :
et on
donne les valeurs numériques suivantes :
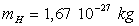 ;
; 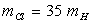 ;
; 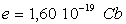 ;
; 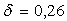
D)1) Qu'appelle t-on barycentre de deux points matériels
? Qu'appelle t-on référentiel barycentrique ?
D)2) L'énergie potentielle d'interaction entre
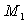 et
et 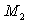 est de la forme :
est de la forme :
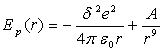 où A
est une constante positive.
où A
est une constante positive.
Quelle signification physique peut-on donner à chacun des deux termes
?
Donner l'allure de la courbe 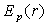 .
Montrer qu'il existe une valeur
.
Montrer qu'il existe une valeur 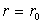 pour laquelle le système est dans une position d'équilibre stable.
En déduire une expression pour la constante A.
pour laquelle le système est dans une position d'équilibre stable.
En déduire une expression pour la constante A.
D)3) On étudie les oscillations libres de la
molécule.
D)3)a) Montrer que le référentiel barycentrique
est galiléen pour le mouvement des deux points matériels si leur
énergie potentielle d'interaction ne dépend que de leur distance.
Exprimer la relation fondamentale de la dynamique dans un référentiel
lié à 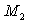 . Pouvait-on
considérer que le référentiel lié à
. Pouvait-on
considérer que le référentiel lié à 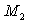 était
galiléen pour le mouvement de
était
galiléen pour le mouvement de 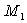 .
.
D)3)b) On pose 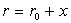 avec
avec 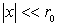 car on se
limite aux mouvements de faible amplitude autour de la position d'équilibre
dans une direction déterminée.
car on se
limite aux mouvements de faible amplitude autour de la position d'équilibre
dans une direction déterminée.
Exprimer l'énergie potentielle  en utilisant un développement limité au deuxième ordre.
en utilisant un développement limité au deuxième ordre.
D)3)c) Exprimer l'énergie cinétique 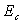 .
A partir de la conservation de l'énergie, en déduire l'équation
différentielle à laquelle obéit la variable x.
.
A partir de la conservation de l'énergie, en déduire l'équation
différentielle à laquelle obéit la variable x.
D)3)d) En déduire la fréquence propre 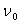 des oscillations libres de la molécule. Application numérique
si
des oscillations libres de la molécule. Application numérique
si 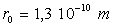 .
.
D)4) On soumet la molécule à un champ
électrique de la forme 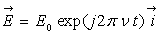 où
où 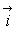 est le vecteur
unitaire de l'axe des x.
est le vecteur
unitaire de l'axe des x.
D)4)a) Etudier le mouvement forcé. En déduire la fréquence
de résonance.
D)4)b) Si n est le nombre de molécules
d'HCl par unité de volume, exprimer le vecteur polarisation créé
par déplacement ionique. Exprimer la dépendance de l'indice optique
avec la fréquence. Que se passe t'il pour 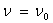 ?
?
| Réponse
D1 | Réponse
D2 | Réponse
D3a | Réponse
D3b | Réponse
D3c | Réponse
D3d | Réponse
D4a | Réponse
D4b |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

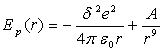 où A
est une constante positive.
où A
est une constante positive.