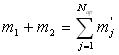Le problème à deux corps
Problème
A) Etude générale
On considère deux particules 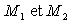 de masses respectives
de masses respectives  repérées, dans un référentiel galiléen d'origine
O, par les vecteurs
repérées, dans un référentiel galiléen d'origine
O, par les vecteurs 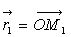 et
et 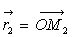 .
.
Nous supposons que ces deux particules sont "seules dans l'espace" c'est à
dire qu'elles forment un système isolé. Il y a donc interaction
entre ces deux particules et nous limitons l'étude au cas où cette
interaction peut être traduite par une fonction scalaire dépendant
de la seule distance r entre les particules soit 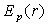 .
Cette fonction est appelée énergie potentielle d'interaction des
deux particules.
.
Cette fonction est appelée énergie potentielle d'interaction des
deux particules.
1) Montrer que les forces qui agissent sur chacune des
particules obéissent au principe de l'action et de la réaction.
2) Ecrire une intégrale première du mouvement.
3) Montrer que le référentiel barycentrique
d'origine G des deux particules est galiléen. En déduire que le
problème se ramène à la résolution d'un problème
à un mobile dont on déterminera la masse 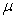 appelée masse réduite.
appelée masse réduite.
On étudiera le cas particulier 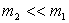 .
.
4)a) Calculer dans le référentiel barycentrique
l'énergie mécanique et le moment cinétique de l'ensemble
des deux particules.
Montrer que l'étude se réduit à celui du mouvement de la
masse réduite dans un référentiel d'origine 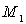 .
.
4)b) A partir du théorème du moment cinétique, montrer
que le mouvement s'effectue dans un plan (on montrera que le moment cinétique
est un vecteur constant que l'on notera 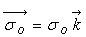 où
où 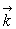 est le vecteur
unitaire perpendiculaire au plan où s'effectue le mouvement).
est le vecteur
unitaire perpendiculaire au plan où s'effectue le mouvement).
5) Pour la suite du problème, on se placera dans
le référentiel barycentrique, les masses  seront notées
seront notées  ,
les points
,
les points 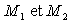 seront
notés O et P.
seront
notés O et P.
On pose 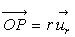 où
où
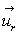 est le vecteur unitaire
de
est le vecteur unitaire
de 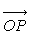 .
.
On étudie dans le référentiel d'origine O, de base
orthonormée directe 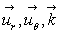 ,
en coordonnées polaires planes
,
en coordonnées polaires planes 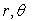 ,
le mouvement du mobile fictif de masse
,
le mouvement du mobile fictif de masse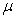 .
.
5)a) Ecrire le moment cinétique et l'énergie mécanique
du mobile fictif. Quel nom donne t’on à la relation 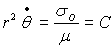 ?
?
En
déduire l'équation différentielle du mouvement.
5)b) Trouver l'équation différentielle ci-dessus à
partir du principe fondamental de la dynamique.
Pour les questions 5)a) et 5)b) on utilisera
implicitement ou explicitement les formules de Binet.
6) Application aux énergies potentielles
d’interaction Ep(r)=k/r
6)a) Exprimer la force d'interaction entre les deux
masses M et m et indiquer le type (attractif ou répulsif)
de cette force suivant le signe de k.
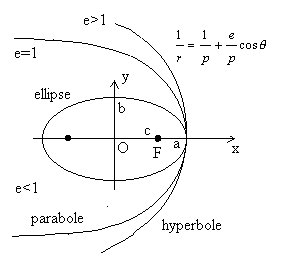
6)b) En remplaçant dans l'équation différentielle
du 5), montrer que la trajectoire de la masse m est une conique
dont l’équation peut être écrite en faisant un bon choix
de l’axe polaire :
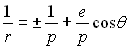
6)c) Exprimer l'énergie mécanique en fonction de 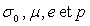 .
.
Discuter la nature de la conique à partir du signe de l'énergie
6)d)
Quelques conséquences pour les orbites elliptiques
- Montrer que l'énergie sur les orbites elliptiques ne dépend
que du grand axe de l'ellipse (elle est en particulier indépendante
de l'excentricité)
- Calculer la quantité
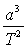 où a est la longueur du demi-grand axe et T la période
de révolution (on exprimera
où a est la longueur du demi-grand axe et T la période
de révolution (on exprimera 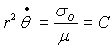 en fonction des paramètres de l'ellipse).
en fonction des paramètres de l'ellipse).
- Qu'en déduisez vous si
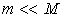 (ce résultat est connu sous le nom de 3ème loi de Képler)
(ce résultat est connu sous le nom de 3ème loi de Képler)
| Réponse
A1 | Réponse
A2 | Réponse
A3 | Réponse
A4a | Réponse
A4b | Réponse
A5a | Réponse
A5b | Réponse
A6a | Réponse
A6b | Réponse
A6c | Réponse
A6d |
B) Etude d’orbites
circulaires
1) En première approximation, on peut considérer
que l’orbite de la Lune autour de la Terre est circulaire de rayon 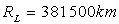 ,
la période de révolution étant
,
la période de révolution étant 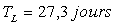 .
.
On admet que le référentiel géocentrique est galiléen
pour le mouvement de la Lune.
1)a) L’interaction Terre-Lune étant de type attraction universelle,
écrire le principe fondamental de la dynamique dans le référentiel
géocentrique.
Déduire une relation entre l’intensité 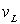 de vitesse de la Lune, la masse
de vitesse de la Lune, la masse 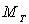 de la Terre et
de la Terre et 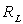 (on appellera
(on appellera 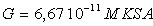 la constante d’attraction universelle).
la constante d’attraction universelle).
1)b) Ecrire une relation entre 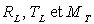 ;
A.N. calculer
;
A.N. calculer 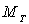
2) Reprendre la question 1) pour la Terre décrivant,
en première approximation, autour du Soleil une orbite circulaire de
150 millions de kilomètres de rayon en 365 jours.
3) On s’intéresse aux satellites géostationnaires.
3)a) Montrer que la trajectoire est un cercle de rayon 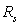 situé dans le plan équatorial.
situé dans le plan équatorial.
3)b) Calculer numériquement la valeur de 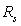 .
.
3)c) Calculer l’énergie mécanique d’un satellite de masse
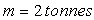 sur son orbite.
Application numérique.
sur son orbite.
Application numérique.
3)d) Calculer l’énergie nécessaire à la satellisation
si la base de lancement est située à une latitude 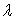 .
Application numérique pour la base de Kourou (
.
Application numérique pour la base de Kourou (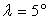 ),
pour la base de Cap Canaveral (
),
pour la base de Cap Canaveral (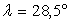 ),
pour la base de Baïkonour (
),
pour la base de Baïkonour (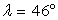 ).
).
Rayon de la Terre 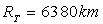
| Réponse
B1a | Réponse
B1b | Réponse
B2 | Réponse
B3a | Réponse
B3b | Réponse
B3c | Réponse
B3d |
C) Etude d’orbites elliptiques
Calcul d’une orbite de transfert
3) Exprimer l’énergie du satellite sur son orbite de transfert,
en déduire les intensités de vitesse 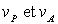 .
.
En déduire l’énergie à communiquer au satellite aux points
P et A ainsi que le temps de transfert pour aller de P à A.
A.N. : L’orbite circulaire basse est celle de première vitesse
cosmique, celle haute correspond à un satellite géostationnaire.
| Réponse
Cot1 | Réponse
Cot2 | Réponse
Cot3 |
Vitesse de libération
1) Faire une représentation des orbites elliptiques
tangentes à la surface de la Terre et montrer que les vitesses à
la surface de la Terre pour ces orbites sont comprises entre deux valeurs que
l'on déterminera.
2) Représenter sur la figure précédente
l'orbite parabolique
3) En Thermodynamique, on apprend que la "vitesse moyenne d'agitation"
des molécules est égale à 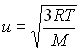 où
où 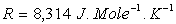
est la constante des gaz parfaits, M la masse molaire et T la
température exprimée en Kelvin. En déduire que l'atmosphère
est stable (ne s'échappe pas de la Terre).
| Réponse
Cvl12 | Réponse
Cvl3 |
Le vaisseau spatial de Youri Gagarine
Le 12 Avril 1961, Youri Gagarine fut le premier cosmonaute
; le vaisseau spatial satellisé était un engin de masse 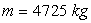 ,
les altitudes du périgée et de l'apogée étaient
respectivement
,
les altitudes du périgée et de l'apogée étaient
respectivement 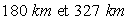 .
.
Calculer les vitesses au périgée et à l'apogée ainsi
que l'énergie nécessaire pour satelliser le vaisseau spatial.
| Réponse
Cyg |
Etude de la chute libre dans un champ d’attraction universelle
Un point matériel 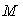 de masse
de masse 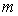 subit
une force attractive de centre
subit
une force attractive de centre 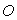 en
en 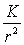 .
.
Lorsqu’il décrit une orbite circulaire autour de O de rayon 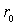 ,
il a une période
,
il a une période 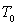 .
.
Déterminer le temps 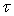 de " chute libre " du point matériel lâché,
sans vitesse initiale, à une distance
de " chute libre " du point matériel lâché,
sans vitesse initiale, à une distance 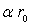 de
de 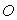 (on exprimera
(on exprimera
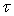 en fonction de
en fonction de
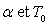 ).
).
| Réponse
Ccl |
D) Etude de trajectoires paraboliques
Comète 1
Une comète est passée en 1843 au voisinage du
Soleil sur une orbite " parabolique ". La distance minimale
comète-soleil a été 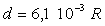 (où R est le rayon de l’orbite terrestre, la Terre décrivant
en première approximation une orbite circulaire autour du Soleil).
(où R est le rayon de l’orbite terrestre, la Terre décrivant
en première approximation une orbite circulaire autour du Soleil).
1) Déterminer la vitesse maximale de la comète.
2) En réalité, l’orbite de la comète est elliptique
et son excentricité est 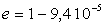 .
En quelle année reviendra t’elle ?
.
En quelle année reviendra t’elle ?
On donne 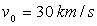 vitesse
de la Terre sur son orbite et
vitesse
de la Terre sur son orbite et 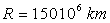 .
.
| Réponse
DC11 | Réponse
DC12 |
Comète 2
|
|
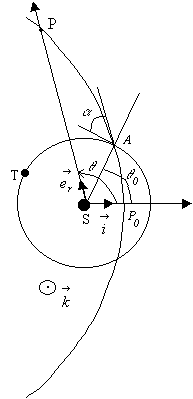
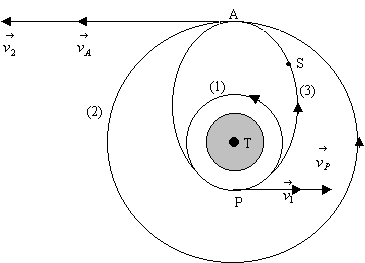
Une comète P de masse 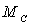 a une trajectoire parabolique dans la plan de l’écliptique.
On rappelle que la Terre T de masse
a une trajectoire parabolique dans la plan de l’écliptique.
On rappelle que la Terre T de masse 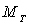 a un mouvement de révolution quasi-circulaire dans ce plan. On
supposera galiléen le référentiel d’origine le centre
S du soleil et que seules les interactions gravitationnelles à
envisager ici sont entre Soleil/Comète et Soleil/Tere. On néglige
l’interaction Comète/Terre.
a un mouvement de révolution quasi-circulaire dans ce plan. On
supposera galiléen le référentiel d’origine le centre
S du soleil et que seules les interactions gravitationnelles à
envisager ici sont entre Soleil/Comète et Soleil/Tere. On néglige
l’interaction Comète/Terre.
On appelle G la constante d’attraction universelle.
1) Sur la trajectoire terrestre de rayon R,
parcourue à vitesse uniforme 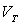 ,
déterminer la relation entre ,
déterminer la relation entre 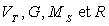 . .
2) L’équation polaire de la trajectoire
est donnée par 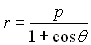 . .
En outre, on rappelle que dans le cas d’une trajectoire parabolique, l’énergie
mécanique totale est nulle. La distance du périhélie
est 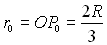 . .
|
2)a) Déterminer le paramètre p
en fonction de R.
2)b) Démontrer que le vecteur 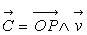 où
où 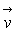 est
le vecteur vitesse de la Comète au point P, est une constante du mouvement
et que
est
le vecteur vitesse de la Comète au point P, est une constante du mouvement
et que 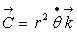
2)c) Déterminer en fonction de 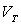 la vitesse maximale
la vitesse maximale 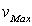 de la Comète. En déduire la valeur de
de la Comète. En déduire la valeur de 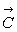 en fonction de
en fonction de  .
.
2)d) Calculer l’angle 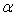 d’intersection des deux trajectoires en A.
d’intersection des deux trajectoires en A.
2)e) Calculer le temps passé par la Comète dans l’orbite
terrestre.
On donne 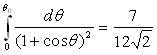
| Réponse
DC21 | Réponse
DC22a | Réponse
DC22b | Réponse
DC22c | Réponse
DC22d | Réponse
DC22e |
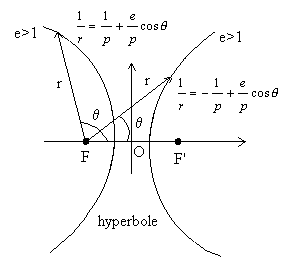
E) Etude de trajectoires hyperboliques
Cas de l’attraction universelle
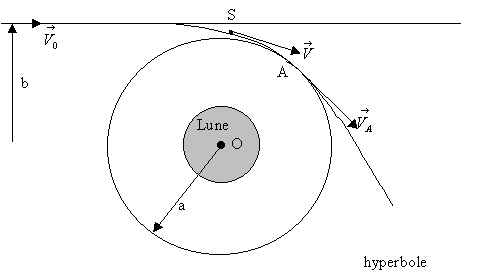
Un vaisseau spatial S de masse m en provenance de la
Terre arrive au voisinage de la lune où l’on supposera qu’il n’est soumis
qu’au seul champ d’attraction lunaire.
La distance d’impact est b et son intensité de vitesse loin de
la lune est 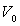 .
.
1) Exprimer l’énergie totale du vaisseau et la constante 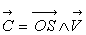 ;
déduire que la trajectoire du vaisseau est hyperbolique.
;
déduire que la trajectoire du vaisseau est hyperbolique.
2) On appelle a la distance minimale d’approche
du vaisseau au centre de la lune (A, sommet de l’hyperbole est tel que
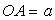 )
)
Etablir une relation entre 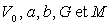 si
G est la constante d’attraction universelle et M la masse de la
Lune ; exprimer cette relation en introduisant
si
G est la constante d’attraction universelle et M la masse de la
Lune ; exprimer cette relation en introduisant 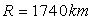 le rayon de la Lune et
le rayon de la Lune et 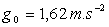 l’intensité de la " pesanteur " à la surface
lunaire).
l’intensité de la " pesanteur " à la surface
lunaire).
A.N. : Calculer 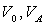 et l’excentricité e de l’hyperbole pour
et l’excentricité e de l’hyperbole pour 
3) Au point A le vaisseau freine " instantanément "
pour décrire une orbite circulaire d’observation de rayon a autour
de la Lune.
Calculer la vitesse 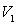 du vaisseau satellisé et l’énergie de freinage nécessaire
du vaisseau satellisé et l’énergie de freinage nécessaire
A.N. : 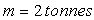
| Réponse
Eau1 | Réponse
Eau2 | Réponse
Eau3 |
Diffusion d'une particule de masse m
de charge positive Z'e par une particule de masse M de charge
positive Ze (expérience de Rutherford)
1) A partir de l'expression de la force coulombienne,
établir l'expression de l'énergie potentielle d'interaction 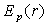 .
.
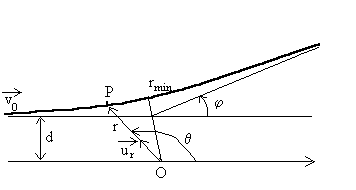
2) Dans un référentiel d'origine O
lié à la particule de masse M , la vitesse au loin de la
particule P de masse m est 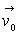 ,
le support de sa direction est à une distance d (paramètre
d'impact) de O.
,
le support de sa direction est à une distance d (paramètre
d'impact) de O.
(La condition m << M n’étant pas réalisée,
il convient pour faire l’étude dans le référentiel d’origine
O d’introduire la masse réduite 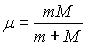 )
)
Déterminer la trajectoire et l'écrire en fonction du paramètre
p et de l'excentricité 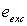 de la conique. On calculera
de la conique. On calculera 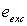 et on en déduira que la trajectoire est une hyperbole.
et on en déduira que la trajectoire est une hyperbole.
3) Exprimer l'énergie mécanique. Retrouver
la nature de la conique.
Déduire la distance minimale 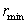 séparant les deux particules.
séparant les deux particules.
4) Déterminer l'angle de déviation 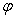 de la particule (Formule de Rutherford).
de la particule (Formule de Rutherford).
Remarque : l’expérience est réalisée
avec des noyaux d’Hélium (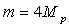 ;
;
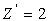 ) diffusant sur
des noyaux d’Or (
) diffusant sur
des noyaux d’Or (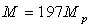 ;
;
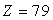 )
)
| Réponse
Eru1 | Réponse
Eru2 | Réponse
Eru3 | Réponse
Eru4 |
F) Atome de Bohr. Spectres de raies de l’atome d’hydrogène.
Détermination de la masse du neutron.
L’électron, de masse 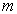 et de charge
et de charge 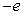 ,
décrit une orbite circulaire de rayon
,
décrit une orbite circulaire de rayon 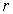 autour du proton de masse
autour du proton de masse 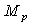 et de charge
et de charge 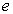 .
L’ensemble (électron + proton) constitue l’atome d’hydrogène que
nous supposerons isolé.
.
L’ensemble (électron + proton) constitue l’atome d’hydrogène que
nous supposerons isolé.
On néglige l’interaction gravitationnelle devant l’interaction électrostatique
entre électron et proton.
1)a) Dans un référentiel lié au
proton, supposé galiléen pour le mouvement de l’électron,
écrire la relation liant la vitesse 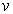 de l’électron et le rayon
de l’électron et le rayon 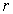 de l’orbite.
de l’orbite.
1)b) Déduire l’expression de l’énergie
mécanique E du système en fonction de r (l’énergie
potentielle à l’infini sera prise comme référence). De
même, déterminer, en fonction de r, l’expression du moment
cinétique de l’électron.
2) Pour expliquer les raies spectrales de l’hydrogène,
on introduit la dualité onde-corpuscule. Le comportement ondulatoire
de l’électron est représenté par une onde de longueur d’onde
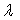 suivant la relation
de De Bröglie
suivant la relation
de De Bröglie 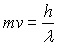 où h est la constante de Planck.
où h est la constante de Planck.
2)a) On postule que l’électron est sur une orbite stable si la
longueur de la circonférence de l’orbite est un nombre de fois entier
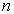 la longueur d’onde.
la longueur d’onde.
Ecrire la relation liant 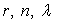 .
.
2)b)
En déduire la relation 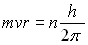 appelée postulat de quantification de Bohr.
appelée postulat de quantification de Bohr.
2)c) Montrer que le rayon de l’orbite est quantifié
(prend des valeurs discrètes) et donner son expression en fonction de
n. De même, montrer que l’énergie est quantifiée
et donner l’expression des niveaux d’énergie en fonction de n.
Application numérique : Calculer, en angström, le
rayon de la première orbite et, en électron-volt, son énergie.
2)d) Quelle est la longueur d’onde du photon émis
dans une transition où le nombre 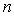 passe de
passe de 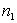 à
à
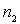 , avec
, avec 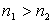 ? (on rappelle que l’énergie d’un photon de fréquence
? (on rappelle que l’énergie d’un photon de fréquence 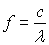 est
égale à hf )
est
égale à hf )
3) En toute rigueur, le référentiel lié
au proton n’est pas galiléen et on se propose d’en mesurer l’effet sur
les longueurs d’onde du spectre.
3)a) Montrer que le référentiel barycentrique du système
proton-électron est galiléen. En déduire que les résultats
précédents demeurent inchangés à condition de remplacer
la masse 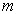 de l’électron
par
de l’électron
par 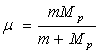 appelée
masse réduite.
appelée
masse réduite.
3)b) Le deutérium est un isotope de l’hydrogène c’est à
dire qu’il est constitué d’un noyau (masse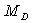 ,
charge e) et d’un électron décrivant une orbite circulaire
autour du noyau.
,
charge e) et d’un électron décrivant une orbite circulaire
autour du noyau.
Soient 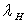 et
et 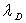 les longueurs d’onde des photons émis, respectivement, par l’hydrogène
et par le deutérium, dans une transition s’effectuant entre deux niveaux
d’énergie caractérisés dans les deux cas par les mêmes
nombres
les longueurs d’onde des photons émis, respectivement, par l’hydrogène
et par le deutérium, dans une transition s’effectuant entre deux niveaux
d’énergie caractérisés dans les deux cas par les mêmes
nombres  .
.
Calculer le rapport 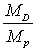 en fonction de
en fonction de 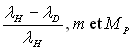 .
En déduire que le noyau du deutérium comporte, par rapport à
celui de l’hydrogène, une particule supplémentaire de charge nulle
et de masse à peu près égale à celle du proton.
.
En déduire que le noyau du deutérium comporte, par rapport à
celui de l’hydrogène, une particule supplémentaire de charge nulle
et de masse à peu près égale à celle du proton.
Application numérique : 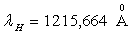 ;
; 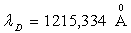
Données numériques générales
:
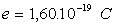 ;
; 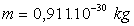 ;
; 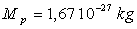 ;
; 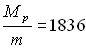 ;
; 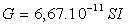 ;
; 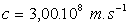 ;
; 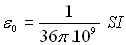 ;
; 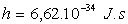
| Réponse
F1a | Réponse
F1b | Réponse
F2a | Réponse
F2b | Réponse
F2c | Réponse
F2d | Réponse
F3a | Réponse
F3b |
G) Collision de particules
(mécanique classique)
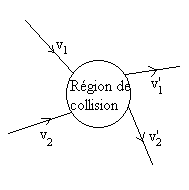
1) La collision de deux particules se manifeste par
une discontinuité dans les vitesses à la traversée d'une
petite région de l'espace où les deux particules se trouvent simultanément
et interagissent fortement.
|
|
Dans le cas d'objets macroscopiques, cette interaction
est due aux forces de contact qui apparaissent lorsque les deux corps
entrent en collision. Dans le cas de particules atomiques ou subatomiques,
il s'agit d'interactions à faible portée.
La connaissance de ce qui se passe pendant la collision elle-même
nécessite une connaissance détaillée de l'interaction.
Notre but n'est pas là, il est plus modeste : connaissant les vitesses
de particules avant la collision, nous désirons obtenir les vitesses
après la collision.
|
Nous supposerons que, avant et après la collision, l'interaction
entre les particules est négligeable et que l'énergie potentielle
correspondante est nulle.
Les masses des particules avant le choc sont  ,
après le choc leur nombre de particules est
,
après le choc leur nombre de particules est 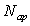 et leurs masses respectives
et leurs masses respectives 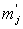 .
La conservation de la masse s'écrit
.
La conservation de la masse s'écrit 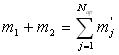
1)1) Ecrire, dans deux référentiels galiléens différents
en translation l'un par rapport à l'autre à vitesse 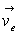 ,
la conservation de l'énergie. En déduire la conservation des quantités
de mouvement avant et après le choc.
,
la conservation de l'énergie. En déduire la conservation des quantités
de mouvement avant et après le choc.
1)2) Etablir les conditions pour que le choc soit élastique
c'est à dire pour qu'il y ait conservation des énergies cinétiques
avant et après le choc.
1)3) La particule de masse 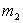 est, avant le choc, au repos, celle de masse
est, avant le choc, au repos, celle de masse 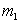 animée d'une vitesse
animée d'une vitesse 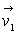 .
Après le choc, les particules sont conservées dans leur structure
interne et leurs vitesses sont respectivement
.
Après le choc, les particules sont conservées dans leur structure
interne et leurs vitesses sont respectivement 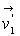 et
et 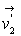 .
.
- Montrer que les vitesses avant et après le choc sont dans un même
plan
- 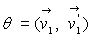 est appelé
angle de diffusion. Etudier les valeurs possibles de
est appelé
angle de diffusion. Etudier les valeurs possibles de 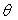 en fonction du rapport
en fonction du rapport 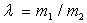 .
Dans le cas d'un choc droit, la particule de masse
.
Dans le cas d'un choc droit, la particule de masse 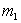 étant un électron, celle de masse
étant un électron, celle de masse 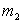 un proton, quelle fraction de l'énergie de l'électron avant le
choc est transférée au proton. Application numérique.
un proton, quelle fraction de l'énergie de l'électron avant le
choc est transférée au proton. Application numérique.
1)4) Dans un pendule balistique articulé autour
d'un axe horizontal, la particule de masse 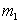 de vitesse
de vitesse 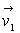 horizontal
vient s'incruster dans la particule de masse
horizontal
vient s'incruster dans la particule de masse 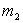 fixée à l'extrémité de la tige, de longueur L,
du pendule. La tige, avant le choc, est verticale et immobile. Après
le choc, elle se déplace d'un angle maximal
fixée à l'extrémité de la tige, de longueur L,
du pendule. La tige, avant le choc, est verticale et immobile. Après
le choc, elle se déplace d'un angle maximal 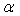 .
En déduire l'intensité de vitesse
.
En déduire l'intensité de vitesse 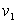 .
.
2) Reprendre la démarche de la question 1)
dans le cas de 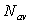 particules incidentes
et de
particules incidentes
et de 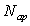 particules après le
choc.
particules après le
choc.
| Réponse
G11 | Réponse
G12 | Réponse
G13 | Réponse
G14 | Réponse
G2 |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
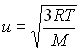 où
où 
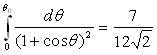

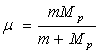 appelée
masse réduite.
appelée
masse réduite.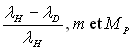 .
En déduire que le noyau du deutérium comporte, par rapport à
celui de l’hydrogène, une particule supplémentaire de charge nulle
et de masse à peu près égale à celle du proton.
.
En déduire que le noyau du deutérium comporte, par rapport à
celui de l’hydrogène, une particule supplémentaire de charge nulle
et de masse à peu près égale à celle du proton.