Mesure de la conductivité et de la diffusivité thermiques
On se propose díétudier un dispositif pour mesurer la
conductivité thermique 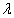 et la diffusivité thermique
et la diffusivité thermique 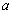 díun matériau.
díun matériau.
La mesure de la conductivité thermique suppose la connaissance du champ
de température permanent dans un dispositif soumis à un flux de
chaleur ; pour la mesure de la diffusivité thermique on envisage
de déterminer les caractéristiques díune onde thermique établie.
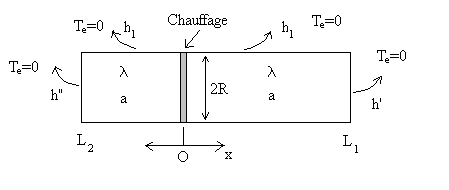
On dispose díun système de chauffage díépaisseur négligeable
délivrant une puissance de chauffage 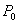 en régime permanent et
en régime permanent et 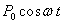 en régime périodique.
en régime périodique.
Ce système est intercalé, comme indiqué sur la figure,
entre les deux échantillons, de même rayon R, de longueurs
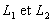 , díun même
matériau dont on veut connaître les caractéristiques thermophysiques.
, díun même
matériau dont on veut connaître les caractéristiques thermophysiques.
Ces deux échantillons sont isolés latéralement et refroidis
à leurs extrémités.
A) Mesure de la conductivité thermique
1) Líisolation latérale est parfaite et les deux échantillons
répondent à líhypothèse de " mur ".
1)a)
On appelle  les
gradients de température dans chacun des échantillons.
les
gradients de température dans chacun des échantillons.
Etablir une relation entre 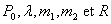 .
.
1)b) Calculer le rapport 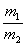 .
.
Peut on espérer que ce rapport soit parfaitement égal à 1
si 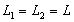 et
et 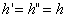 ?
2) Líisolation latérale níest pas parfaite et cette imperfection
est caractérisée par un coefficient díéchanges latéral
?
2) Líisolation latérale níest pas parfaite et cette imperfection
est caractérisée par un coefficient díéchanges latéral
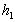 .
.
2)a) A quelle condition doit obéir 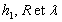 pour valider líhypothèse de " barre " dans les échantillons.
pour valider líhypothèse de " barre " dans les échantillons.
2)b) Cette condition étant remplie, on se limite au cas particulier
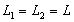 et
et 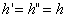 et on néglige tout résistance thermique de contact entre les échantillons
et le chauffage.
et on néglige tout résistance thermique de contact entre les échantillons
et le chauffage.
Etablir le champ de température 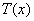 [identique dans chacun des échantillons] en fonction de
[identique dans chacun des échantillons] en fonction de 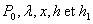 .
.
Montrer que líon retrouve le champ de température correspondant à
líhypothèse de " mur " si 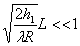 .
.
| Réponse
A1a | Réponse
A1b | Réponse
A2a | Réponse
A2b |
B) Mesure de la diffusivité thermique
1) Ecrire le bilan thermique correspondant à un champ de température
variable, líisolation latérale étant imparfaite et caractérisée
par 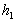 .
.
On pose 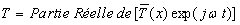 ,
écrire líéquation différentielle vérifiée
par
,
écrire líéquation différentielle vérifiée
par 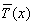 .
.
2) La pulsation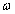 et
la longueur des échantillons sont telles que líon puisse considérer
ceux-ci comme semi-infinis.
et
la longueur des échantillons sont telles que líon puisse considérer
ceux-ci comme semi-infinis.
En déduire que le champ de température périodique dans chacun
des échantillons est de la forme : 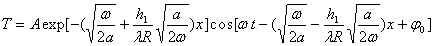 si la condition
si la condition 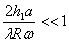 est réalisée.
est réalisée.
3) Peut on mesurer la diffusivité thermique ?
| Réponse
B1 | Réponse
B2 | Réponse
B3 |
