La température ambiante
-
-
-
-
-
-
Analyse thermique d'un système
Le fond d'un récipient métallique (type "
casserole ") est soumis à un flux de chaleur uniforme de densité
![]() .
.
La température ambiante ![]() sera prise comme référence et on notera :
sera prise comme référence et on notera :
- ![]() la conductivité
thermique du récipient,
la conductivité
thermique du récipient,
- ![]() l'épaisseur
des parois,
l'épaisseur
des parois,
- ![]() le rayon du
récipient,
le rayon du
récipient,
- ![]() la hauteur du
récipient,
la hauteur du
récipient,
- ![]() le coefficient
d'échanges thermiques latéral (paroi cylindrique vertical),
le coefficient
d'échanges thermiques latéral (paroi cylindrique vertical),
- ![]() le coefficient
d'échanges thermiques sur le fond intérieur du récipient.
le coefficient
d'échanges thermiques sur le fond intérieur du récipient.
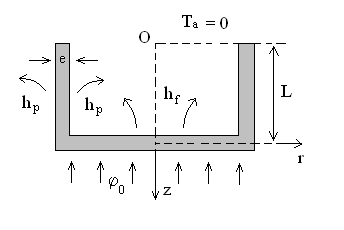
On désire analyser le champ de températures permanent dans le récipient.
1) Dans une première analyse, on ne considère
que le fond en forme de disque de rayon R et d'épaisseur e,
la température notée ![]() étant considérée uniforme.
étant considérée uniforme.
A partir d'un bilan thermique, calculer l'expression de ![]() .
A.N.
.
A.N.
2) Dans une deuxième analyse, on considère
le fond et la paroi cylindrique supposées à température
uniforme (notation ![]() ).
).
A partir d'un bilan thermique, calculer l'expression littérale de ![]() .
A.N.
.
A.N.
Indiquer pourquoi la première analyse donne une température
trop élevée, pourquoi la deuxième analyse donne une température
trop faible.
3) Dans une troisième analyse, on suppose que
le fond est à température uniforme notée ![]() et que la partie cylindrique se comporte comme une ailette de longueur L
en contact thermique parfait avec le fond.
et que la partie cylindrique se comporte comme une ailette de longueur L
en contact thermique parfait avec le fond.
Justifier l'hypothèse d'ailette (ou de " barre thermique ")
à partir du nombre de Biot.
On appellera ![]() le
flux de chaleur évacué par la partie cylindrique.
le
flux de chaleur évacué par la partie cylindrique.
Ecrire l'équation de bilan thermique pour la partie cylindrique (on appellera
![]() le champ de température).
le champ de température).
Résoudre cette équation en négligeant tout échange
de chaleur à l'extrémité libre de la partie cylindrique.
En déduire ![]() et, par un bilan thermique, l'expression littérale de
et, par un bilan thermique, l'expression littérale de ![]() .
.
Montrer que :
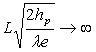
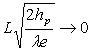
Calculer numériquement ![]() pour les conditions du problème.
pour les conditions du problème.
4) L'analyse du champ de températures dans la
partie cylindrique est conservée. En ce qui concerne le champ de température
pour le fond, il est supposé uniforme dans l'épaisseur la paroi
et à symétrie de révolution. Il sera noté ![]() .
.
Ecrire les équations de bilan thermique pour ![]() ainsi que les équations aux limites nécessaires.
ainsi que les équations aux limites nécessaires.
On ne résoudra pas le système d'équations.
| Réponse 1 | Réponse 2 | Réponse 3 | Réponse 4 |