On se propose de comprendre les phénomènes thermiques lors de la glaciation (évolution de l’épaisseur d’une plaque de glace) d’une nappe d’eau suite à un refroidissement brutal.
On supposera, dans toute l’étude, que les phénomènes thermiques sont unidimensionnels (direction cartésienne x) et que le milieu étudié peut être considéré comme semi-infini.

1) Dans cette première partie, on suppose que le refroidissement impose, en , à partir du temps , une température constante [] inférieure à la température de changement de phase eau-glace.

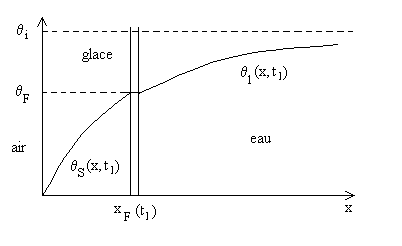
La courbe ci-dessus donne une représentation du champ de température à un instant donné .

1)1) Ecrire les équations régissant le champ de température dans la glace et dans l’eau.
On note la température initiale (supposée uniforme) de la nappe d’eau.
On négligera :

• le changement de masse volumique entre la glace et l’eau au cours de la glaciation,
• les mouvements convectifs à l’intérieur de la phase liquide eau.

De façon systématique, les paramètres sont indicés avec la lettre pour la glace et la lettre pour l’eau et on note la chaleur latente massique de fusion de la glace.

Données numériques :  ;  ; ;  ;  ; ;
 ; ;  ;
On montrera en particulier que le bilan thermique à la traversée de l’interface glace-eau s’écrit :

1)2) On souhaite déterminer à chaque instant la position du " front de glaciation ", c’est à dire de l’interface eau-glace.
1)2)a) On cherche une solution de l’équation de la chaleur dans la glace en utilisant le changement de variable proposé par Cauchy : où est la diffusivité de la glace.
De même, on cherche une solution de l’équation de la chaleur dans l’eau en utilisant le changement de variable proposé par Cauchy : où est la diffusivité de l’eau.
1)2)b) Montrer, à partir de l’équation de continuité de la température, sur le front de glaciation , que ces solutions sont possibles si et si .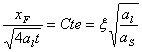
1)2)c) Montrer, à partir de l’équation de bilan thermique à la traversée de l’interface eau-glace, que la valeur du paramètre se déduit de la résolution de l’équation transcendante : où est l’effusivité thermique, et .

Lorsque la température initiale de l’eau est égale à , la résolution numérique de cette équation conduit aux résultats suivants :

Pour : ,

• calculer l’épaisseur de la glace,
• comparer, à tout instant, les densités de flux thermique dans la glace et dans l’eau au front de glaciation.

1)2)d) Montrer à partir des conclusions précédentes que :
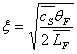ð 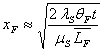constitue une solution approchée du problème tout à fait acceptable.

2) Lors d’hivers particulièrement rigoureux, on peut constater, dans la région nantaise, des refroidissements semblables à celui étudié dans la question 1).
L’eau de la rivière Erdre, assimilable à une nappe d’eau au niveau du quai de Versailles, gèle et une épaisseur de glace de l’ordre de se forme en deux heures.
Cette valeur très éloignée de celle trouvée ( en une heure) en 1) remet en cause la théorie faite et en particulier la condition de température imposée en .

2)1)
2)1)a) Réécrire les équations régissant le champ de température dans la glace et dans l’eau en tenant compte d’un coefficient d’échange à l’interface air atmosphérique-glace
2)1)b) On ne cherche pas à résoudre ce système d’équations (le lecteur pourra essayer pour constater qu’il n’y a pas de solution analytique) mais à le simplifier compte tenu de ce que nous a appris la partie 1) : on peut raisonnablement négliger le flux de conduction dans l’eau.
Ecrire le nouveau système d’équations
2)1)c) Pour simplifier, à nouveau ce système d’équations, on compare à partir de la question 1), le temps de formation d’une épaisseur de glace à la constante de temps maximale d’un mur conductif d’épaisseur .
En déduire que le temps de formation d’une épaisseur de glace est prépondérant et que l’on peut considérer que le champ de température dans la glace est, à chaque instant, en " régime permanent ".
Etablir, à partir d’un bilan thermique de la congélation d’une couche d’eau d’épaisseur , l’équation différentielle liant et .

2)1)d) Résoudre cette équation différentielle.
Etudier le cas particulier
A.N. . Calculer l’épaisseur de glace formée au bout d’une heure

3) Dans cette troisième partie, on s’intéresse à la glaciation de sol.
Sec, le sol a une masse volumique égale à . Gorgé d’eau, il a une masse volumique à . La conductivité thermique du sol glacé sera prise égale à
3)1) Calculer la chaleur latente massique de fusion du sol glacé .
On pourra introduire pour faire ce calcul la notion de porosité (défini dans le sol sec ou gorgé d’eau ou glacé comme le rapport du volume occupé par l’air ou l’eau ou la glace au volume occupé par le sol).
On montrera aussi que la masse volumique du sol glacé est pratiquement égale à celle du sol gorgé d’eau.
3)2) Dans les conditions d’un hiver nantais où la moyenne journalière des températures ne descend pas en dessous de , combien de jours consécutifs devraient avoir lieu pour que la glaciation du sol se fasse sur une profondeur de  ?

| Réponse 11 | Réponse 12a | Réponse 12b | Réponse 12c | Réponse 12d | Réponse 21a | Réponse 21b | Réponse 21c | Réponse 21d | Réponse 31 | Réponse 32 |