Mesure de la diffusivité thermique
par la méthode flash
(Corrections à apporter à la méthode suivant
les conditions expérimentales)
1)
![]() ;
;
![]() ;
; ![]() ;
;
![]()
Recherche d’une solution en ![]()
Nous cherchons la fonction ![]() sous la forme :
sous la forme : ![]() avec
avec ![]()
En dérivant par rapport à ![]() ,
,
![]() on obtient :
on obtient :
![]() ð
ð
![]()
![]() ;
;
![]()
![]()
![]() ð
ð ![]() ð
ð ![]() ð
ð ![]()
ð ![]() ð
ð ![]()
![]() ð
ð ![]() ð
ð ![]()
On intègre cette dernière expression par rapport
à la variable ![]() .
Le calcul est classique et se fait par parties pour ce qui concerne la fonction
erf.
.
Le calcul est classique et se fait par parties pour ce qui concerne la fonction
erf.
On obtient : ![]()
![]() ð
ð ![]()
En ce qui concerne la condition ![]() ,
nous adoptons la visualisation ci-après.
,
nous adoptons la visualisation ci-après.
|
|
|
Pour ![]() ,
on obtient
,
on obtient ![]() et
la solution cherchée s’obtient comme la limite, quand
et
la solution cherchée s’obtient comme la limite, quand ![]() ,
de :
,
de :
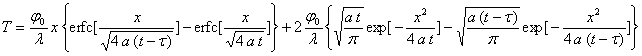 ð
ð
![]()
Utilisation de la transformée de Laplace
![]() ;
;
![]() ;
; ![]() ;
;
![]()
ð ![]() ;
;
![]() ;
; ![]() avec
avec ![]()
La résolution
de ce système donne : ![]() dont l’original est directement dans les tables,
dont l’original est directement dans les tables, ![]() .
.
Utilisation des fonctions de Green
![]() ;
;
![]() ;
; ![]() ;
;
![]()
La fonction de Green associé à ce problème
est :
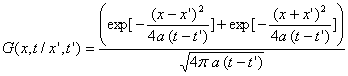
La solution sera trouvée à partir de :
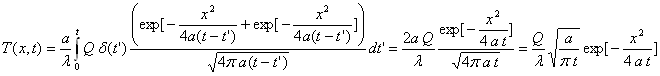
Exploitation
La recherche du temps ![]() où se produit le maximum de la température en une abscisse
où se produit le maximum de la température en une abscisse ![]() se calcule à partir de la relation,
se calcule à partir de la relation,
![]() ð
ð
![]() ð
ð
![]()
Cette dernière constitue
une méthode classique de mesure de la diffusivité d’un matériau
où on n’a pas besoin de connaître la valeur de la température.
2)
Recherche d’une solution en ![]()
Dans la question 1), nous avons traité cette
question (nous ne pouvions faire autrement avec la méthode en ![]() .
Nous avons trouvé pour
.
Nous avons trouvé pour ![]() ,
,
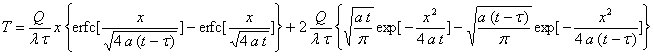
Utilisation de la transformée de Laplace
![]() ;
;
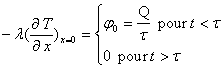 ;
; ![]() ;
;
![]()
ð ![]() ;
;
![]() ;
; ![]() avec
avec ![]()
La résolution de ce système donne : ![]() dont l’original est presque directement dans les tables. Il convient, pour la
deuxième partie de l’original, d’appliquer le théorème
du retard,
dont l’original est presque directement dans les tables. Il convient, pour la
deuxième partie de l’original, d’appliquer le théorème
du retard, 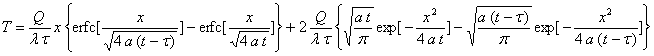
Utilisation des fonctions de Green
![]() ;
; 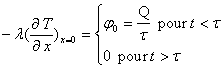 ;
; ![]() ;
; ![]()
La fonction de Green associé à ce problème
est :
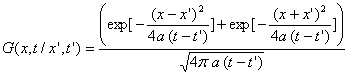
La solution sera trouvée à partir de :
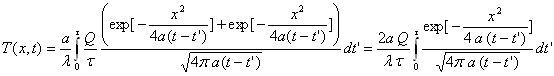
Le calcul de cette intégrale est un peu fastidieux.
Nous posons ![]() ð
ð
![]()
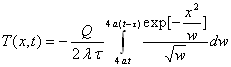
Cette intégrale se fait par parties. On obtient :
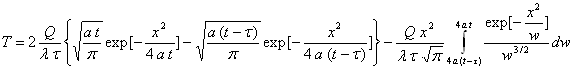
Pour cette dernière intégrale, on pose
![]() ð
ð
![]() ð
ð
![]()
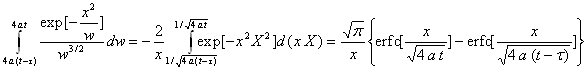
En reportant, on obtient
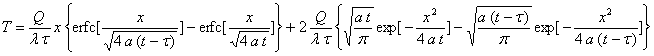
Exploitation
La recherche du temps ![]() où se produit le maximum de la température en une abscisse
où se produit le maximum de la température en une abscisse ![]() se calcule à partir de la relation,
se calcule à partir de la relation,
![]() ð
ð
![]() ð
ð
![]() avec
avec ![]()
Si![]() ,
, ![]() et
et ![]() ð
ð
![]()
3)
![]() ;
;
![]() ;
; ![]() ;
;
![]()
Recherche d’une solution en ![]()
Nous ne connaissons pas de méthode pour calculer la solution analytique
Utilisation de la transformée de Laplace
Compte tenu de 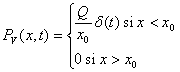 ,
l’espace doit être séparé en deux suivant que l’on se situe
pour
,
l’espace doit être séparé en deux suivant que l’on se situe
pour ![]() ou
ou ![]() .
.
Pour ![]()
ð
![]() ;
; ![]() avec
avec ![]()
Pour ![]()
ð
![]() ;
; ![]() avec
avec ![]()
La continuité de la température et du flux de
chaleur imposent :
![]() et
et ![]()
La résolution de ces deux systèmes liés
ne présente guère de difficultés. On obtient,
![]()
![]()
Ces deux images ont un même original, à savoir
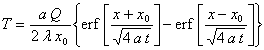
Utilisation des fonctions de Green
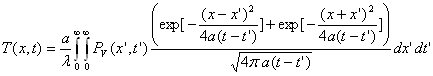
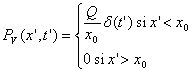 ð
ð 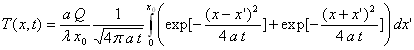
On pose ![]() ð
ð ![]() et
et ![]() ð
ð
![]()
ð 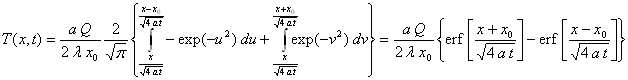
Exploitation
La recherche du temps ![]() où se produit le maximum de la température en une abscisse
où se produit le maximum de la température en une abscisse ![]() se calcule à partir de la relation,
se calcule à partir de la relation,
![]() ð
ð
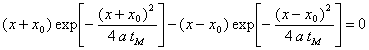
ð 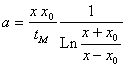 ð
ð 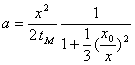 si
si ![]()
4)
![]() ;
;
![]() ;
; ![]() ;
;
![]()
Ce système d’équations peut être traité
par superposition de deux systèmes d’équations en posant :
![]() où
où
![]() ;
; ![]() ;
;
![]() ;
; ![]()
et
![]() ;
; ![]() ;
;
![]() ;
; ![]()
Le système ![]() a été résolu dans la question 1).
a été résolu dans la question 1). ![]()
La solution du système ![]() doit être recherchée.
doit être recherchée.
Recherche d’une solution en ![]()
Nous ne connaissons pas de méthode pour calculer la solution analytique
Utilisation de la transformée de Laplace
Compte tenu de 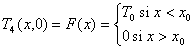 ,
l’espace doit être séparé en deux suivant que l’on se situe
pour
,
l’espace doit être séparé en deux suivant que l’on se situe
pour ![]() ou
ou ![]() .
.
Pour ![]()
ð ![]() ;
;
![]() avec
avec ![]()
Pour ![]()
ð ![]() ;
;
![]() avec
avec ![]()
La continuité de la température et du flux de
chaleur imposent :
![]() et
et ![]()
Les équations obtenues sont identiques à celles obtenues dans
la question 3) à condition d’identifier ![]() et
et ![]() .
.
On obtiendra donc : 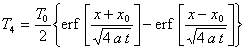
Utilisation des fonctions de Green
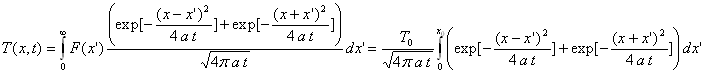
Cette dernière intégrale est identique à celle calculée
dans la question 3) à condition d’identifier ![]() et
et ![]() .
.
On obtiendra donc : 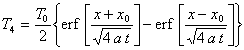
La solution complète sera donc :
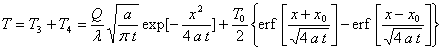
5)
![]() ;
;
![]() ;
; ![]() ;
;
![]()
Recherche d’une solution en ![]()
Dans la question 1), nous avons d’abord cherché ![]() puis intégré le résultat.
puis intégré le résultat.
Nous étendons cette méthode en cherchant la fonction
![]() qui est solution
du système d’équations,
qui est solution
du système d’équations,
![]() ;
; ![]() ;
;
![]() ;
; ![]()
Nous avons vu dans la question 1) la forme générale de
la solution, ![]()
![]() ð
ð
![]()
En ce qui concerne la condition ![]() ,
nous adoptons la visualisation ci-après.
,
nous adoptons la visualisation ci-après.
|
|
|
Pour ![]() ,
on obtient
,
on obtient ![]() et
la solution cherchée s’obtient comme la limite, quand
et
la solution cherchée s’obtient comme la limite, quand ![]() ,
de :
,
de :
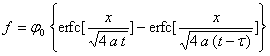 ð
ð
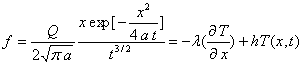
Il convient de faire l’intégration par rapport à
la variable ![]() de
cette équation différentielle du premier ordre avec second membre
non nul.
de
cette équation différentielle du premier ordre avec second membre
non nul.
Pour faire cette intégration, nous appliquons la méthode de la
variation de la constante, c'est-à-dire que la solution se présente
sous la forme générale
![]()
En remplaçant dans l’équation différentielle,
on obtient :
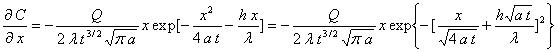
Nous posons ![]() ð
ð ![]()
ð ![]()
ð ![]()
ð
![]()
![]() ð
ð ![]() ð
ð ![]()
Utilisation de la transformée de Laplace
![]() ;
; ![]() ;
; ![]() ;
; ![]()
ð ![]() ;
;
![]() ;
; ![]() avec
avec ![]()
La résolution de ce système donne : 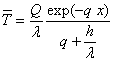 dont l’original est directement dans les tables,
dont l’original est directement dans les tables,
![]() .
.
Utilisation des fonctions de Green
![]() ;
;
![]() ;
; ![]() ;
;
![]()
Dans le cours de Conduction mis à disposition sur le
net, la fonction de Green associée à ce système d’équations
n’est pas indiquée. Il est recommandé de calculer la fonction
![]() , solution du
système d’équations,
, solution du
système d’équations,
![]() ;
; ![]() ;
;
![]() ;
; ![]()
et de procéder à l’intégration de l’équation différentielle
comme il a été fait dans la méthode en ![]() .
.
La fonction de Green associé au système d’équations
![]() (condition limite
de type température imposée) est :
(condition limite
de type température imposée) est :
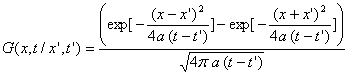
ð ![]()
La solution sera trouvée à partir de :
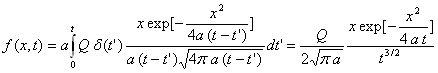
L’intégration, pour calculer ![]() a été faite et conduit à :
a été faite et conduit à :
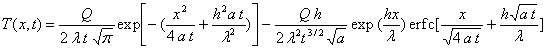
Remarques