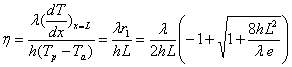; h tient compte des échanges de chaleur par convection et par
rayonnement thermique1)
; h tient compte des échanges de chaleur par convection et par
rayonnement thermique
2)1) Un bilan thermique en régime permanent entre
une section 
s'écrit
:
Pour l'ailette à section constante : 
2)2) 
;
2)3) 
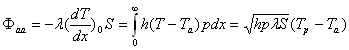
3) 
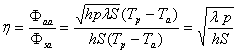
Ailette à section rectangulaire : 
;
puisque 
;
Ailette à section circulaire : 
;
;
4) Lorsque l'on se rapproche de l'extrémité
, la température
dans l'ailette se rapproche de la température du fluide et l'ailette
échange de moins en moins. De plus la surface d'échange à
l'extrémité étant faible par rapport à la surface
latérale de l'ailette, les échanges de chaleur à l'extrémité
seront faibles devant les échanges latéraux. On remarquera enfin
que faire le calcul avec une condition " flux de chaleur nul à l'extrémité
" revient à calculer une température de l'extrémité
plus forte qu'elle n'est réellement et donc à minimiser les échanges
avec ailette c'est à dire à faire un calcul pessimiste sur l'efficacité
de l'ailette. Ainsi la condition trouvée pour justifier l'approximation
" ailette semi-infinie " sera, de fait, mieux assurée.
Les équations régissant le problème seront
:
; 
; 
La solution est :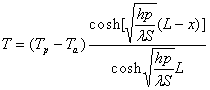 
Le flux de chaleur échangé par l'ailette est
donnée par : 
soit l'efficacité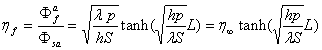 
.
L'approximation " ailette semi-infinie " est justifiée
si 
.
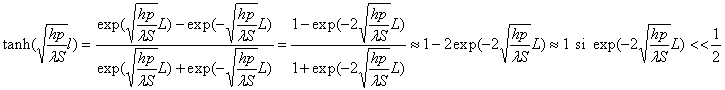
soit 
5) Le traitement de l'équation bilan du 2)1)
donne :
Soit 
ð 
Calcul de 
; 
Le profil parabolique donne la forme de 
avec 
ð 
L'équation différentielle bilan devient : 
La recherche de solution sous la forme 
conduit à l'équation caractéristique :
soit deux racines 
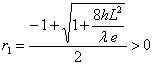et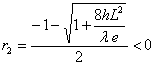 
et à la solution générale 
La température doit rester finie en 
a pour conséquence 
L'écriture de 
donne la solution : 
L'efficacité sera égale à 