On considère une paroi à température au contact d’un fluide à température .

1) Exprimer la densité de flux de chaleur échangée entre la paroi et le fluide si h est le coefficient d'échanges de chaleur (on précisera les modes d'échanges de chaleur intervenant dans h).
| Réponse 1 |

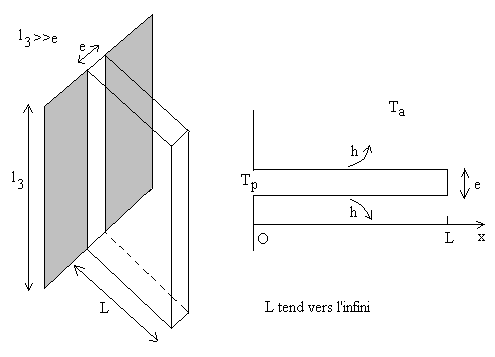
2) On place sur une partie de cette paroi une ailette de section constante (figure ci-après). On notera respectivement p et S le périmètre et la section de l’ailette.
2)1) Etablir, à partir d’un bilan énergétique, l’équation différentielle qui régit le champ de température permanent [on considérera qu’en chaque section le champ de température peut, en première approximation, être pris uniforme].
| Réponse 21 |
2)2) Ecrire les équations aux limites en et
| Réponse 22 |

2)3) Déterminer le champ de température  ; en déduire le flux de chaleur échangé entre l’ailette et le fluide.
| Réponse 23 |

3) En déduire l’efficacité rapport du flux de chaleur échangé par l'ailette au flux échangé par la paroi sans ailette pour une même section.
Que deviennent les résultats précédents pour une ailette semi-infinie de section constante à symétrie de révolution de rayon R.
| Réponse 3 |

4) On désire apprécier l'approximation " ailette semi-infinie ".
Expliquer pourquoi on peut raisonnablement se limiter à un calcul où la condition prise en consistera à négliger les échanges de chaleur à cette extrémité.
Montrer que, sous cette condition, l'efficacité de l'ailette finie est égale à . En déduire une condition justifiant l'approximation " ailette semi-infinie ".
| Réponse 4 |

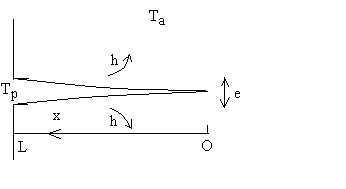
5) Reprendre le bilan énergétique dans le cas d'une ailette à profil parabolique.

| Réponse 5 |