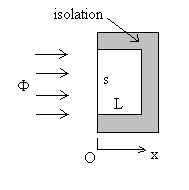
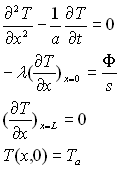Etude d'un fluxmètre
1) Dans une première analyse, on néglige
le phénomène de conduction de la chaleur. Le champ de température
 dans l’échantillon
est donc indépendant de l’abscisse
dans l’échantillon
est donc indépendant de l’abscisse 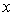 .
.
A partir d’un bilan thermique, montrer que 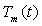 évolue
linéairement avec le temps.
évolue
linéairement avec le temps.
A.N. Calculer 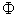 si
si 
2) On ne néglige plus le phénomène
de conduction, le champ de température est noté 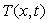 .
.
a)
Justifier les équations qui régissent ce champ de température,
à savoir :
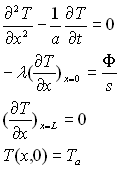
b) La résolution du système d’équations conduit à :
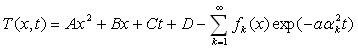 où les
où les 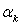 forment une suite infinie de valeurs croissantes positives.
forment une suite infinie de valeurs croissantes positives.
En déduire que la constante de temps du système est 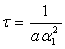 .
.
Donner un ordre de grandeur pour 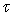 et indiquer à partir de quel temps
et indiquer à partir de quel temps 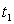 on peut considérer que
on peut considérer que 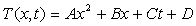 .
.
c)
Montrer à partir du système d’équations que 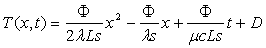 .
En déduire qu ‘il est possible de déterminer la quantité
.
En déduire qu ‘il est possible de déterminer la quantité
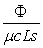 à partir
de l’enregistrement de la température en un point quelconque de l’échantillon.
à partir
de l’enregistrement de la température en un point quelconque de l’échantillon.
3) Le flux de chaleur 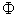 est un flux de chaleur par rayonnement réalisé en plaçant
en face de l’échantillon un disque de surface
est un flux de chaleur par rayonnement réalisé en plaçant
en face de l’échantillon un disque de surface 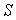 à température
à température 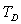 d’émissivité
d’émissivité 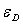 .
.
a) Calculer le facteur de forme échantillon-disque 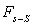 si
si 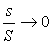 . En déduire
que
. En déduire
que 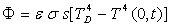 si
si 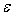 est l’émissivité de la surface de l’échantillon.
est l’émissivité de la surface de l’échantillon.
b) La température de la face du disque est égale à
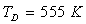 . En déduire
que dans les premiers instants le flux
. En déduire
que dans les premiers instants le flux 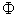 est constant et que la solution en 2)c) est justifiée.
est constant et que la solution en 2)c) est justifiée.
Pour une élévation de 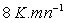 ,
calculer
,
calculer  .
.
c)
Expliquer comment seraient affectés les résultats précédents
si la condition 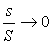 n’était plus réalisée (on pourra s’aider de l’analogie
électrique).
n’était plus réalisée (on pourra s’aider de l’analogie
électrique).

| Réponse
1 | Réponse
2a | Réponse
2b | Réponse
2c | Réponse
3a | Réponse
3b | Réponse
3c |
![]() ;
;
![]() ), de forme
cylindrique (section
), de forme
cylindrique (section ![]() ;
épaisseur
;
épaisseur ![]() )
est thermiquement parfaitement isolée latéralement et sur
sa face arrière
)
est thermiquement parfaitement isolée latéralement et sur
sa face arrière ![]() .
.![]() reçoit un flux de chaleur
reçoit un flux de chaleur ![]() .
Initialement l’échantillon est à la température ambiante
.
Initialement l’échantillon est à la température ambiante
![]() .
.