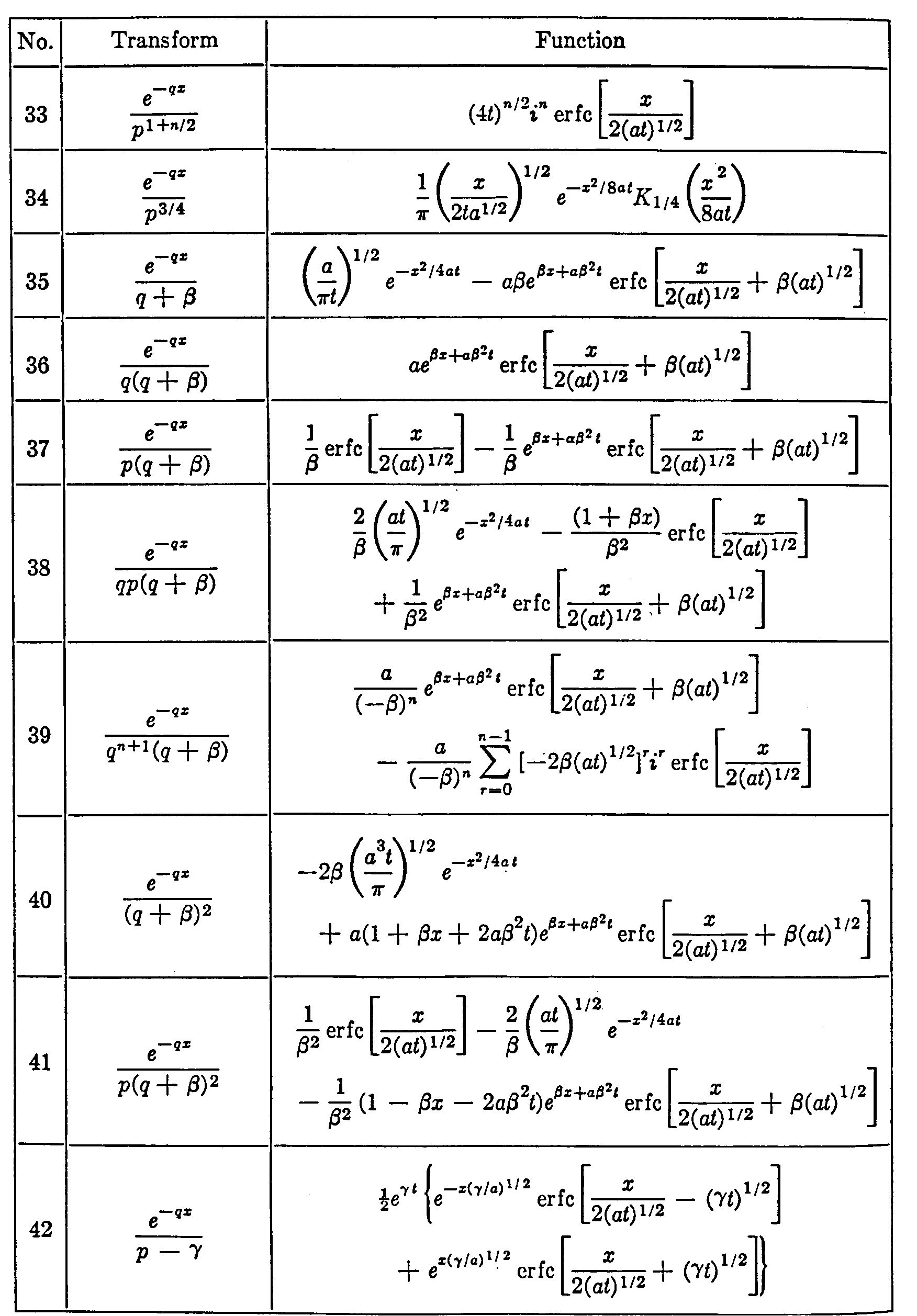CHAPITRE 6 : Résolution par utilisation de la transformée de Laplace
Plan
1. Définition de la Transformée de
Laplace et conditions d’existence>/a>
2.Propriétés de la Transformée
de Laplace
3. Utilisation de la Transformée de Laplace
à partir de Tables
4. Inversion numérique de la Transformée
de Laplace
5. Inversion analytique de la Transformée
de Laplace
Tables de Transformées de Laplace
1. Définition de la Transformée de Laplace et conditions d’existence
1.1. Définitions préalables
1.1.1. Une fonction f(t) est dite " continue par morceau
" sur un domaine fini ![]()
1.2. Définition de la Transformée de Laplace et conditions d’existence
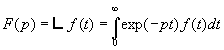 où
p est complexe
où
p est complexe
- l’existence de F(p) suppose la convergence de l’intégrale
- on dit que F(p) est " l’image " de f(t)
2. Propriétés de la Transformée de Laplace
On note ![]() la
fonction dite " image " de f(t) et
la
fonction dite " image " de f(t) et ![]() la
fonction dite " original " de F(p).
la
fonction dite " original " de F(p).
Sous réserve des conditions d’existence, la correspondance ![]() est unique (le calcul de f(t) connaissant F(p)
-retour à l’original- sera examiné plus tard).
est unique (le calcul de f(t) connaissant F(p)
-retour à l’original- sera examiné plus tard).
2.1. Linéarité
Si ![]() alors
alors ![]() ; la démonstration est évidente à partir de la définition
de la transformée de Laplace.
; la démonstration est évidente à partir de la définition
de la transformée de Laplace.
Exemple :![]() ð
ð![]() où u(t) est la fonction échelon unité.
où u(t) est la fonction échelon unité.
2.2. Transformée de Laplace de la fonction dérivée
Si f(t) est continue, alors ![]() où
où ![]() ; la démonstration est évidente à partir de la définition.
; la démonstration est évidente à partir de la définition.
Plus généralement, si f(t) est discontinue aux points ![]()
![]()
Les expressions ci-dessus se généralisent aux dérivées
" d’ordre n " et, en particulier, si la fonction f(t) et
ses dérivées sont continues, on obtient :
![]()
Exemple :![]() ð
ð![]()
soit ![]()
2.3. Transformée de l’intégrale 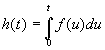
![]() ; on pose
; on pose ![]()
![]() ð
ð![]()
En généralisant, on obtient 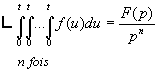
Exemple :![]() ð
ð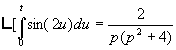
2.4. Dérivation et intégration par rapport à un paramètre a
Soit 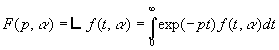 ð
ð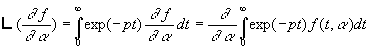
d’où ![]()
Soit  ð
ð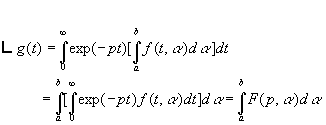
d’où 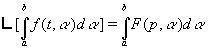
Exemples :
- ![]() ð
ð![]()
- ![]() ð
ð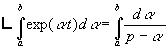 ð
ð![]()
2.5. Théorème du retard
Soit ![]() alors
alors 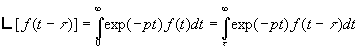
En faisant le changement de variable![]() ,
on montre que
,
on montre que ![]()
Transformée de Laplace d’un créneau unité de
largeur t ; cas limite de la fonction
de Dirac
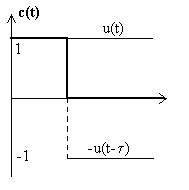 |
Le cas limite où
|
2.6. Transformée de Laplace d’une fonction périodique
Soit une fonction f(t) périodique de période T,
on définit ![]() afin de pouvoir écrire
afin de pouvoir écrire ![]()
Si G(p) est la transformée de Laplace de g(t),
alors F(p) la transformée de f(t) s’écrit
![]()
ð![]()
Exemple : Train d’impulsion de hauteur A, de largeur![]() ,
de période T ð
,
de période T ð![]()
2.7. Théorème de l’amortissement
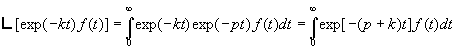
d’où ![]()
Exemple :![]() ð
ð![]()
2.8. Changement d’échelle de temps (similitude)
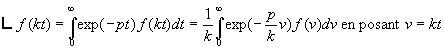
d’où ![]() avec, évidemment, k positif.
avec, évidemment, k positif.
Exemple :![]() ð
ð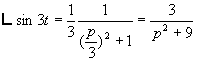
2.9. Dérivation et intégration de la fonction symbolique F(p)
 ð
ð 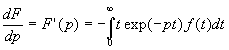
Exemple :![]() ð
ð![]()
 ð
ð 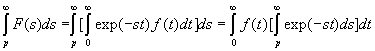
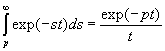
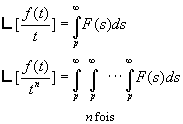
L’équation 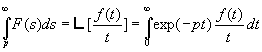 devient, dans le cas particulier p = 0,
devient, dans le cas particulier p = 0,
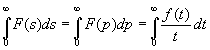
Exemples :
- ![]() ð
ð
-  se calcule
à partir de
se calcule
à partir de ![]() dont l’image est
dont l’image est ![]() ð
ð
-  se calcule
à partir de
se calcule
à partir de ![]() dont l’image est
dont l’image est ![]() ð
ð
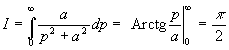
2.10. Comportements asymptotiques

Si ![]() , alors
, alors ![]() et on obtient
et on obtient ![]()
Exemple :![]() ;
; ![]()
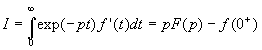
Si 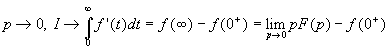 ð
ð![]()
2.11. Le Théorème de convolution
On appelle convolution de deux fonctions f(t) et g(t),
la fonction h(t) définie par 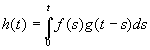 que l’on note h(t) = f * g .
que l’on note h(t) = f * g .
Cette opération est commutative, c’est à dire que 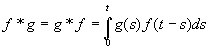
On démontre que ![]()
Exemple : Calculer l’original de ![]() sachant que
sachant que ![]() et que
et que ![]()
Le théorème de convolution donne 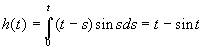
Evidemment, pour cet exemple, il est plus rapide de remarquer que :
![]() (immédiat)
(immédiat)
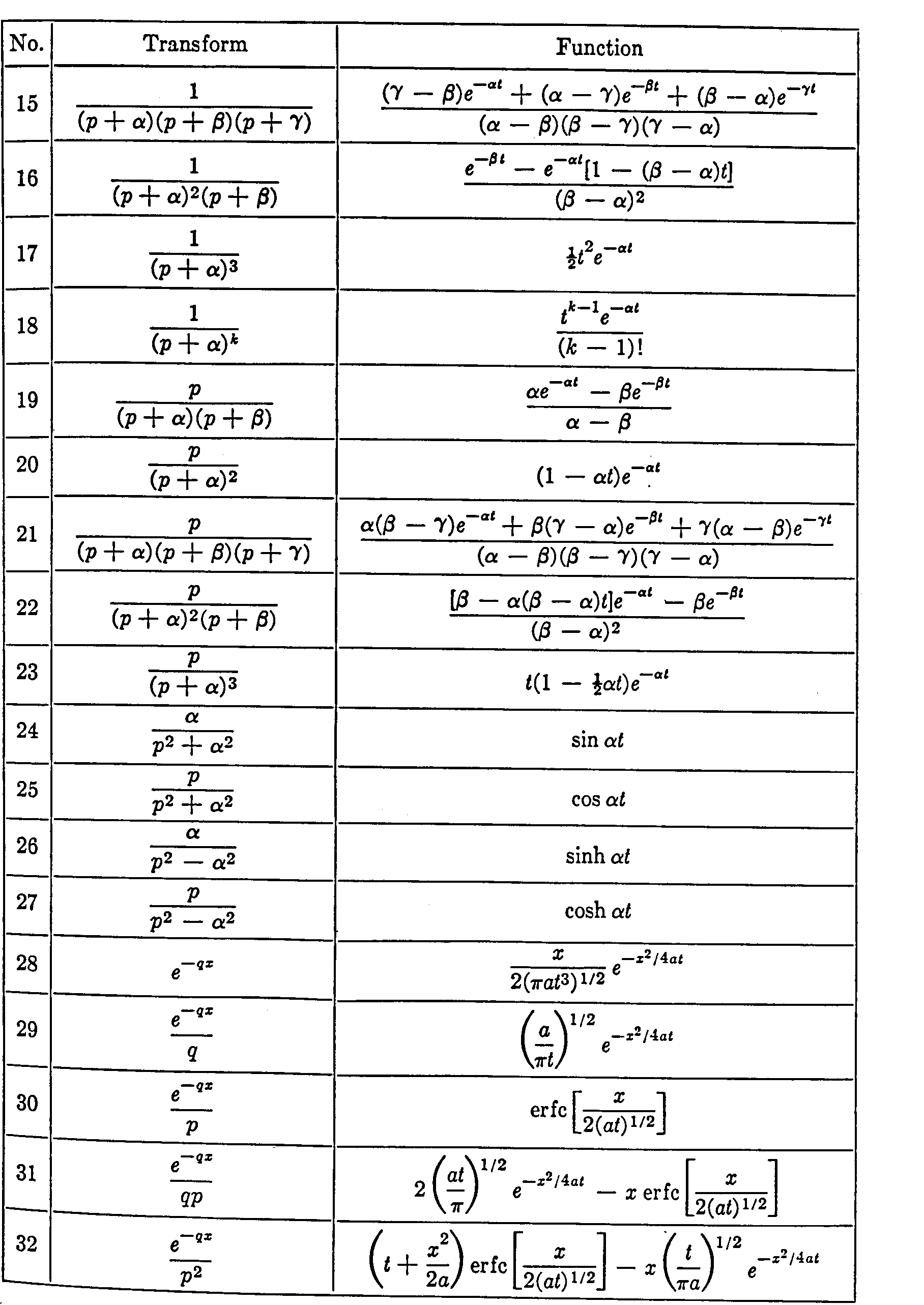
3. Utilisation de la transformée de Laplace à partir des Tables
Dans la pratique, pour un problème donné, on obtient assez
facilement l’image F(p), la véritable difficulté
se trouve dans la recherche de la fonction f(t) origine.
Cette recherche est aidée par l’existence de Tables de correspondances
très complètes ![]() qui
s’utilisent comme un " dictionnaire " mais dont la manipulation demande de l’expérience
pour appliquer judicieusement les propriétés de la Transformée.
qui
s’utilisent comme un " dictionnaire " mais dont la manipulation demande de l’expérience
pour appliquer judicieusement les propriétés de la Transformée.
A défaut de pouvoir appliquer ces tables, il convient d’avoir recours
au théorème d’inversion dontla mise en oeuvre se révèle,
souvent, lourde.
Ce théorème appelé aussi " formule d’inversion
de Mellin-Fourier " s’écrit :
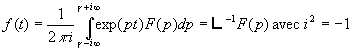
Cette intégrale se calcule à l’aide du théorème
des Résidus, ![]() est une constante réelle supérieure aux abscisses de tous les
points singuliers de F(p). Nous traiterons de l’application du
théorème d’inversion dans le paragraphe 5 de ce chapitre, pour
la suite immédiate de ce chapitre nous utilisons les Tables de Transformées
extraites de l’excellent ouvrage de V. ARPACI " Conduction Heat Transfer " édité
chez Addison-Wesley
est une constante réelle supérieure aux abscisses de tous les
points singuliers de F(p). Nous traiterons de l’application du
théorème d’inversion dans le paragraphe 5 de ce chapitre, pour
la suite immédiate de ce chapitre nous utilisons les Tables de Transformées
extraites de l’excellent ouvrage de V. ARPACI " Conduction Heat Transfer " édité
chez Addison-Wesley
3.1. Première règle de Heaviside
Soit ![]() développable
en série de Mac Laurin.
développable
en série de Mac Laurin.
Sachant que ![]() ,
on obtient
,
on obtient ![]()
La correspondance étant réversible, dans la pratique
on recherche un développement en série de F(p)
et on trouve f(t).
Exemple :![]()
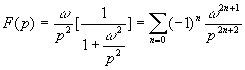
On sait que ![]() ,
donc
,
donc ![]()
et par suite ![]()
3.2. Deuxième règle de Heaviside
![]() est une fraction
rationnelle, c’est à dire que P et Q sont des polynômes.
On impose que le degré du polynôme Q soit supérieur
au degré du polynôme P.
est une fraction
rationnelle, c’est à dire que P et Q sont des polynômes.
On impose que le degré du polynôme Q soit supérieur
au degré du polynôme P.
Il suffit de décomposer F(p) selon les règles
usuelles et de revenir à f(t) par inversion immédiate
de chaque terme.
Exemple 1 :![]() ð
ð![]()
Exemple 2 :![]() ð
ð![]()
3.3. Exemples empruntés à la Conduction de la Chaleur
3.3.1. Remarques générales
 ð
ð![]()
Par suite ![]() ð
ð![]() voir tables formule n° 30
voir tables formule n° 30
Soit ![]() ð
ð![]() (voir tables)
(voir tables)
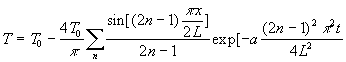 , série
de Fourier difficilement utilisable pour les temps faibles.
, série
de Fourier difficilement utilisable pour les temps faibles.
Ce même problème traité par la transformée de Laplace
donne ![]() .
La fonction origine (qui est la série ci-dessus) ne se trouve pas dans
les tables et son calcul nécessite l’utilisation du théorème
d’inversion.
.
La fonction origine (qui est la série ci-dessus) ne se trouve pas dans
les tables et son calcul nécessite l’utilisation du théorème
d’inversion.
Une méthode intéressante consiste à faire un développement
en série de l’image ![]() .
.
![]()
![]() ð
ð![]()
L’original ![]() figure dans les tables.
figure dans les tables.
Cette dernière solution est adaptée aux les temps faibles pour lesquels le développement en série peut être limité aux premiers termes si L est suffisamment grand, soit aussi t suffisamment petit.
![]() ;
; ![]() ;
;
![]() ;
; ![]()
Une recherche de la solution sous la forme ![]() conduit
à :
conduit
à :
![]()
![]()
On obtient ![]()
Pour trouver ![]() ,
on utilise la technique de la transformée de Laplace.
,
on utilise la technique de la transformée de Laplace.
 , soit encore
, soit encore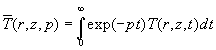
![]()
On en déduit ![]() et
et ![]()
![]() ð
ð![]()
L’original de ![]() se
calcule à partir de la formule n° 43 des tables et du théorème
de l’amortissement.
se
calcule à partir de la formule n° 43 des tables et du théorème
de l’amortissement.
Ainsi, ![]()
3.4. Comportement des solutions pour les " faibles " temps ou pour les temps " suffisamment élevés "
On rappelle les théorèmes (valables si les limites existent)
: ![]() et
et ![]() si
bien que l’original de la transformée obtenue en faisant p grand
donne le comportement pour les faibles temps (c’est à dire aussi pour
les milieux semi-infinis) et que l’original de la transformée obtenue
pour p faible donne le comportement pour les temps élevés.
si
bien que l’original de la transformée obtenue en faisant p grand
donne le comportement pour les faibles temps (c’est à dire aussi pour
les milieux semi-infinis) et que l’original de la transformée obtenue
pour p faible donne le comportement pour les temps élevés.
On comprendra l’intérêt de ces propos sur un exemple.
Exemple :![]() correspond à la transformée de Laplace d’un mur initialement à
température de référence, soumis sur sa face x =
0 à un échelon de température
correspond à la transformée de Laplace d’un mur initialement à
température de référence, soumis sur sa face x =
0 à un échelon de température ![]() dont on maintient la face x = L à la température de référence.
dont on maintient la face x = L à la température de référence.
Il existe plusieurs méthodes approchées pour calculer
la valeur numérique de l’original f(t) à partir
de sa transformée F(p). Dans le cas de fonctions f(t)
monotones
la plus simple est la suivante :
![]() où il
suffit de remplacer la variable p par
où il
suffit de remplacer la variable p par ![]() pour obtenir f(t) avec une excellente précision. On trouvera
ci-après les valeurs numériques
pour obtenir f(t) avec une excellente précision. On trouvera
ci-après les valeurs numériques ![]() .
.
Cette technique, que nous avons utilisée à maintes reprises,
est très performante dans des situations complexes où il
est " impossible " d’obtenir une solution exacte.
Pour permettre au lecteur d’en juger, nous prenons l’exemple d’un tube métallique
de rayons intérieur et extérieur respectivement égaux à ![]() et
et ![]() . Les
échanges de chaleur sur la face extérieure du tube sont caractérisés
par un coefficient h et une température du milieu extérieur
. Les
échanges de chaleur sur la face extérieure du tube sont caractérisés
par un coefficient h et une température du milieu extérieur ![]() .
A l’intérieur, un milieu conductif de conductivité thermique
.
A l’intérieur, un milieu conductif de conductivité thermique![]() est
en contact parfait avec le tube (sous certaines conditions, le milieu à
l’intérieur du tube peut être un fluide au repos).
est
en contact parfait avec le tube (sous certaines conditions, le milieu à
l’intérieur du tube peut être un fluide au repos).
Nous considérons que les échanges de chaleur sont radiaux
et supposons la paroi du tube métallique suffisamment faible pour
négliger les gradients de température dans celle-ci.
Le système à résoudre est le suivant :
![]()
où ![]() diffusivité
du milieu conductif,
diffusivité
du milieu conductif, ![]() ,
,  et
et ![]() .
.
On obtient sans difficulté 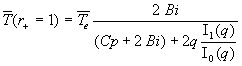 .
On conçoit facilemment que, aussi simple que soit
.
On conçoit facilemment que, aussi simple que soit ![]() ,
l’original ne se trouve pas dans les Tables et que l’inversion analytique est,
évidemment, très lourde.
,
l’original ne se trouve pas dans les Tables et que l’inversion analytique est,
évidemment, très lourde.
Par contre, l’utilisation de l’inversion numérique se montre
particulièrement efficace.
5. Inversion analytique de la Transformée de Laplace
Si 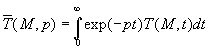 est
la transformée de Laplace de
est
la transformée de Laplace de ![]() ,
on démontre réciproquement le théorème d’inversion
appelé " formule d’inversion de Mellin-Fourier " :
,
on démontre réciproquement le théorème d’inversion
appelé " formule d’inversion de Mellin-Fourier " :
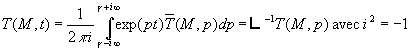
Dans cette formule, l’intégration est effectuée sur la
droite Cette droite laisse à sa " gauche " tout point singulier de |
 |
5.1. Rappels sur les fonctions ![]() de la variable complexe
de la variable complexe ![]()
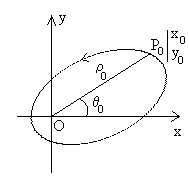 |
En effet La valeur 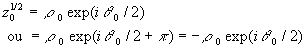
Il existe donc deux expressions de Dans le plan |
Si on fait un tour complet autour de l’origine O, c’est à dire si ![]() fait un tour complet pour revenir au point de départ, alors
fait un tour complet pour revenir au point de départ, alors ![]() et
et ![]() .
.
Exemple 2 : la fonction ![]() est
multiforme
est
multiforme
En effet, nous pouvons choisir ![]() puisque
puisque ![]() quelque soit k entier.
quelque soit k entier.
Ainsi ![]() a
une infinité de valeurs.
a
une infinité de valeurs.
Partant de P0 , chaque fois que l’on
fait un tour autour de O, la détermination change.
De manière générale, pour éviter ce problème
et rendre la fonction uniforme (c’est à dire à valeur unique),
on pratique une coupure dans le plan complexe comme indiqué
sur la figure dans le cas du contournement du point origine.
 |
Ainsi partant de P0
, on décrite la courbe fermée (G)
pour revenir en P0 et |
5.2. Le théorème des résidus
Soit, dans le plan complexe, un domaine (R) délimité par
le contour fermé (G).
Si, en ![]() ,
il existe, pour la fonction
,
il existe, pour la fonction ![]() ,
un pôle d’ordre k, le théorème des résidus
permet d’écrire
,
un pôle d’ordre k, le théorème des résidus
permet d’écrire 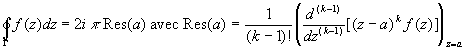
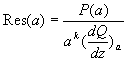
Il s’agit de calculer ![]() dans le plan complexe (voir figure 1).
dans le plan complexe (voir figure 1).
La droite verticale (B) d’abscisse ![]() (réel)
sera prise telle que
(réel)
sera prise telle que ![]() soit suffisamment grand pour que toutes les singularités de
soit suffisamment grand pour que toutes les singularités de ![]() se trouvent à sa gauche.
se trouvent à sa gauche.
5.3.1. Cas n° 1
![]() est holomorphe
exceptée en des points singuliers qui constituent les n pôles
situés à gauche de la droite (B). Cette circonstance, pour les
problèmes de Conduction de la Chaleur, se produit généralement
dans les milieux limités.
est holomorphe
exceptée en des points singuliers qui constituent les n pôles
situés à gauche de la droite (B). Cette circonstance, pour les
problèmes de Conduction de la Chaleur, se produit généralement
dans les milieux limités.
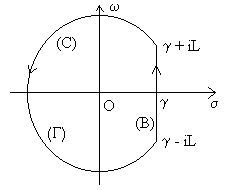 |
On utilise le contour fermé (G)
constitué de la droite (B) et du cercle (C) de centre O et de rayon
L où L et 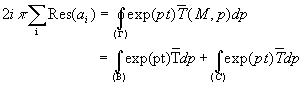 |
Si nous faisons tendre L vers l’infini, l’intégrale suivant (C)
portion de cercle de rayon L tend vers 0 et on obtient  de la fonction
de la fonction ![]() .
.
Exemple :![]() ð
ð![]()
Les pôles sont ![]() et
et ![]() qui
sont des pôles simples.
qui
sont des pôles simples.
On utilise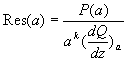 et
on obtient :
et
on obtient :![]()
Finalement, 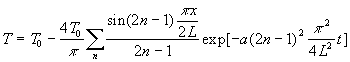
5.3.2. Cas n° 2
Au cas n° 1, il convient d’ajouter un branchement en ![]()
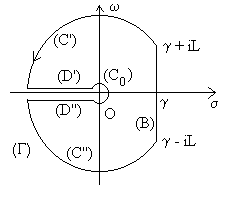 |
Le contour (G) devient
constitué de (B), (C’), (D’), (C0),
(D’’) et (C’’).
Lorsque nous ferons tendre L vers l’infini, les intégrales suivant les portions de cercle (C’) et (C’’) tendront vers 0. Par contre, il conviendra de calculer les autres intégrales et le calcul devient très lourd. En Conduction de la Chaleur, ce cas se produit pour les milieux semi-infinis. On comprendra tout l’intérêt des tables pré-établies dans le cas de résolution par la transformée de Laplace. |
Pour illustrer nos propos, nous prenons l’exemple de ![]() pour lequel le pôle
pour lequel le pôle![]() est un point de branchement. Après un long calcul, on peut montrer que
l’original est
est un point de branchement. Après un long calcul, on peut montrer que
l’original est ![]() .
.
Tables de Transformées de Laplace