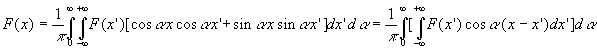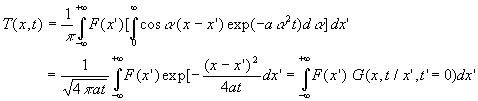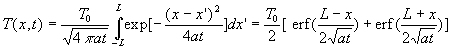CHAPITRE 4 : Les régimes transitoires
Plan
1. Exemples
2. Autres exemples
3. Equation de type " ailette "
4. Conclusions sur les régimes transitoires
dans les milieux finis. Constante de temps
5. Orthogonalisation dans les milieux semi-infinis
6. Orthogonalisation dans les milieux infinis
Les régimes transitoires correspondent à l’évolution
d’un système d’un état initial (permanent ou en équilibre)
vers un état final (permanent ou en équilibre) provoquée
par un changement à l’instant initial des sources; le champ de température 
dépend du champ de température initial 
mais l’influence de clui-ci s’estompe avec le temps. A l’instant initial, au
moins une source change, par contre elles demeurent constantes ensuite.
Les régimes transitoires ne doivent pas être confondus
avec les régimes variables pour lesquels les sources évoluent
au cours du temps.
Le champ de températures est régi par le système d’équations
: 
La méthode générale de résolution par les
fonctions de Green ne peut être envisagée sans posséder
une bonne maîtrise préalable de la technique de séparation
de variables avec développement en série de fonctions orthogonales.
A partir d’exemples, comme il a été fait dans le chapitre
2, nous allons nous initier et nous perfectionner à cette technique.
Remarque : dans tous ces exemples, les dimensions restent finies, le cas de dimensions semi-infinies ou infinies sera traité séparément.
1.1. Exemple 1 : la condition initiale n’est pas homogène
 |
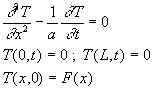Il s’agit du cas simple d’un mur sans sources internes.
Au temps t = 0 , on change les sources externes. Dans le cas traité, on impose une température de référence sur les faces du mur, la température initiale n’étant pas à cette température de référence. |
Dans un premier temps, la méthode consiste à chercher
une solution à variables séparées, c’est à
dire sous la forme 
.
Le report dans l’équation aux dérivées partielles conduit
à 
en tenant compte du fait que le premier terme ne dépend que de x
et que le second ne dépend que de t .
Par intégration, en tenant compte des conditions aux limites
dans la direction x, on obtient :
et 
Remarque : le choix du signe devant 
est imposé par le fait que 
doit rester fini quelque soit t ; cette remarque impose à la direction
spatiale d’être homogène pour conduire à une infinité
de valeurs propres.
Dans un deuxième temps, le système d’équations
étant linéaire, on cherche une solution sous la forme d’une combinaison
linéaire 
.
La dernière condition aux limites s’écrit 
Le dernier temps consiste à déterminer 
par la méthode des fonctions orthogonales.
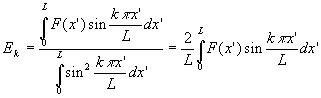
Le champ de température s’écrit alors :
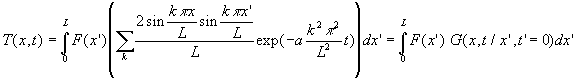
Remarque : la fonction 
sera la fonction de Green du problème pour 
.
1.2. Exemple 2 : la direction spatiale n’est pas homogène
 |
Par rapport à l’exemple 1, la condition initiale a été rendue homogène et une condition aux limites sur la direction x n’est pas homogène. |
Le lecteur vérifiera que la méthode appliquée sur
l’exemple 1 conduit à une impasse.
En fait, cette méthodologie n’est applicable que pour :
système
3 Pour rendre le système d’équations de l’exemple 2 en système
3, on utilise la superposition des solutions (linéarité des équations)
en cherchant une solution sous la forme 
où 
est le champ de température final indépendant du temps.
Le champ de température 
est régi par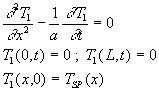 
Par différence le champ de température
sera régi par 
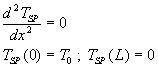
La solution est immédiate 
Le calcul de 
est
une application directe de l’exemple 1, on obtient :
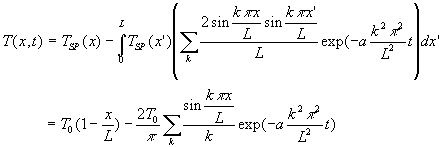
1.3. Exemple 3 : l’équation aux dérivées partielles
n’est pas homogène
 |
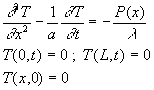Par rapport à l’exemple 1, la condition initiale a été rendue homogène et l’équation aux dérivées partielles n’est pas homogène. |
Pour rendre le système d’équations de l’exemple 3 en système
3, on utilise la superposition des solutions (linéarité des équations)
en cherchant une solution sous la forme 
où 
est le champ de température final indépendant du temps.
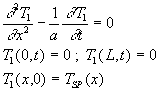ð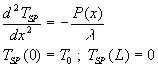
Pour déterminer 
,
la connaissance explicite de P(x) est nécessaire.
Si 
ð
Le calcul de est
une application directe de l’exemple 1, on obtient :
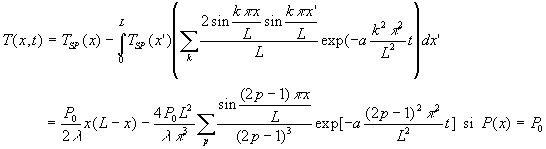
1.4. Exemple 4 : exemple 1 + exemple 2 + exemple 3
 |
Compte tenu des raisonnements, la solution de
l’esemple 4 est la superposition des solutions des exemples 1, 2 et 3.
Une autre méthodologie aurait été de chercher une solution particulière aux équations de l’exemple 4 pour obtenir un système 3 d’équations. |
La solution particulière serait évidemment 
Remarque préliminaire : la superposition de solutions (avec recherche de solutions particulières) transforme le système d’équations en un système de type 3, on ne traite que des systèmes d’équations de ce dernier type.
2.1. Champ de température 
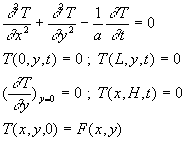ð
ð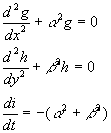
Après intégration et application des conditions aux limites,
on obtient :
; 
; 
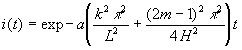
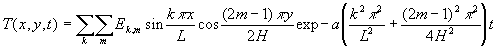
Le calcul de 
se
fait à partir de 
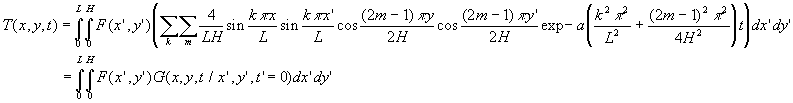
Remarque importante :
La fonction propre 
apparait
comme le produit des fonctions propres :
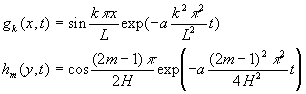
On obtient ces deux fonctions propres si on traite chacune des directions
x et y de manière indépendante.
Ce résultat est général et pourra être utilisé
pour un champ de température 
2.2. Champ de température à symétrie de révolution 
La séparation de variables 
conduit
à 
Par intégration, on obtient 
Il convient d’avoir deux conditions homogènes suivant la direction
r .
Le cas particulier du cylindre plein conduit à la simplification 
car la température doit rester finie en 
(
).
A titre d’exemple, nous choisissons ce cas particulier et la condition 
Cette dernière condition devient 
et conduit à l’équation transcendante
.
Par suite, 
,
le calcul de 
se
fait à partir de 
,
on obtient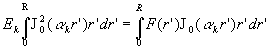 
.
Compte tenu de l’équation transcendante,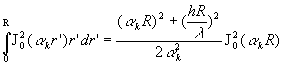 
et
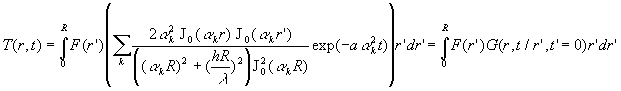
Le cas particulier 
ð
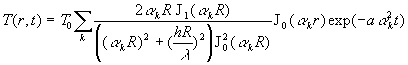
Remarques :
- le lecteur aura noté l’introduction de la fonction de pondération 
,
- l’identité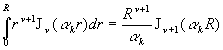 
est très utilisée.
2.3. Champ de température à symétrie de révolution 
Il convient de raisonner à partir 
en
faisant un rapprochement avec l’exemple du paragraphe 2.1. ou d’utiliser la
remarque du paragraphe à savoir 
produit
de fonctions propres suivant les directions indépendantes r et
z .
Le lecteur pourra, à titre d’exemple, coupler les problèmes
traités dans les paragraphes 1.1. et 2.2.
2.4. Champ de température à coordonnées cylindriques
La séparation de variables 
conduit
à 
La suite du calcul est particulière, le lecteur se reportera avec intérêt au paragraphe 1.3.5.4. du chapitre 2.
se calcule à
partir de 
est possible [
].
En reportant, on obtient : 
ð
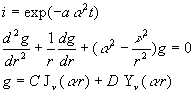
Le calcul redevient classique, les conditions aux limites suivant la direction
r fournissent les valeurs 
,
celles suivant j les valeurs de 
.
Nous nous limitons à un exemple où 
r = 0 ð D = 0 car 
ð
Nous imposons, en plus, la condition 
qui implique les équations transcendantes 
où 
permet le calcul des coefficients,
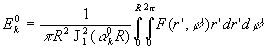
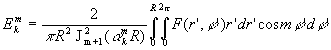
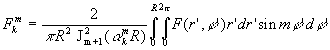
2.5. Champ de température à coordonnées cylindriques 
Il convient de raisonner à partir 
en tenant compte du paragraphe 2.4. ou d’utiliser la remarque du paragraphe
2.1. à savoir 
produit de fonctions propres suivant les directions 
d’une part et z d’autre part.
2.6. Champ de température à symétrie shérique
Le mieux, pour cette équation aux dérivées partielles,
est de faire la transformation 
qui conduit à 
.
Cette dernière équation est celle du mur.
ð
Le cas particulier de la sphère pleine conduit nécessairement
à 
A titre d’exemple, nous choisissons ce cas particulier et la condition qui
s’écrit 
.
La méthodologie est habituelle, on obtient 
avec l’équation transcendante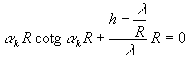 
.
L’application de la condition initiale donne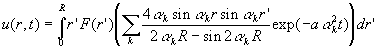 
et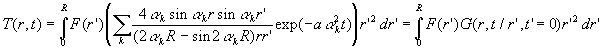 
2.7. Champ de température à coordonnées sphériques 
La séparation de variables 
conduit à :
avec 
ð
ð
ð
Nous ne donnons pas d’exemple, le lecteur pourra se reporter au chapitre 2 paragraphe 1.3.5.7.
2.8. Champ de température à coordonnes sphériques 
La résolution de ce type de problème fait apparaitre les Polynômes associés de Legendre et ne sera pas envisagée.
3. Equation de type " ailette "
La recherche d’une solution à variables séparées 
entraine 
et 
.
Le problème sur les dimensions spatiales est inchangé, quant à
celui suivant le temps il consiste à changer 
.
4. Conclusions sur les régimes transitoires dans les milieux finis. Constante de temps
Le champ de température évolue d’un état initial
à un étal final indépendant du temps.
Pour illustrer nos propos, nous prenons l’exemple traité dans le paragraphe
12 où à un mur, initialement à température uniforme
prise comme référence, on impose sur la face x = 0 une
température 
,
l’autre face x = L étant maintenue à température
de référence.
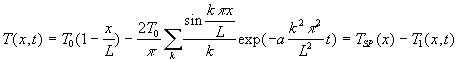représente
le champ de température calculé.
Il est constitué de deux termes, le premier 
indépendant du temps (régime final permanent), le second [
]
sous forme d’une série dépendant de l’espace et du temps. Ce second
terme devient nul pour un temps suffisant ( lorsque 
). 
représente,
ici, l’évolution du champ de température de l’état final
à l’état initial.
Les figures ci-après représentent :
- le champ de température en fonction de x pour différentes
valeurs du temps,
- le champ de température en fonction du temps pour une abscisse
x
fixée.
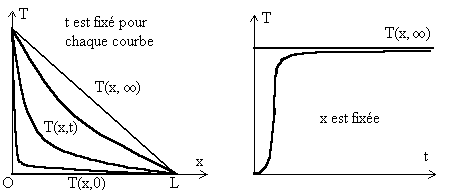
Mis à part les premiers instants, le champ de température se
présente sous la forme 
car
on peut se limiter au premier terme de la série.
La constante 
est, par définition, la constante de temps du système thermique.
Elle joue un rôle important car elle fixe l’échelle de temps, en
particulier on peut dire que la phase transitoire est terminée si 
.
La constante de temps augmente avec les dimensions du système,
est inversement proportionnelle à la diffusivité thermique
et dépend des conditions aux limites.
Dans le cas particulier considéré, 
Nous illustrons nos propos sur l’exemple :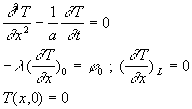 
où un mur, initialement à température uniforme prise comme
référence, est soumis sur sa face x = 0 à une densité
de flux de chaleur continue, la face x = L étant parfaitement
isolée.
La chaleur entrant régulièrement par une face n’étant
pas évacuée, il ne peut exister de régime permanent
(indépendant du temps).
La recherche d’une solution (la direction x n’étant pas
homogène) s’appuie sur l’existence d’une solution particulière
dépendant de l’espace et du temps.
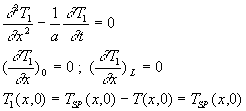ð
ð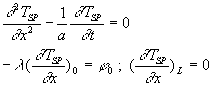
Il n’existe pas de méthode générale pour trouver une solution
particulière. Dans le cas présent, on cherche 
sous
forme de série de puissance en x et en t.
On obtient 
La recherche de la solution 
est
classique.
.
Le calcul des coefficients se fait à partir de 
Après calculs,
Passé un temps suffisant, le champ de température devient asymptotique
et égal à 
.
La notion de constante de temps reste valide, pour le cas particulier
étudié elle est égale à 
.
5. Orthogonalisation dans les milieux semi-infinis
5.1. Milieu semi-infini cartésien ( 0 < x < ¥ )
La recherche d’une solution à variables séparées
(en tenant compte de la condition en x = 0) conduit à :
Dans le cas d’un mur fini d’épaisseur L, on obtient une suite
infinie de valeurs discrétes pour 
qui se rapprochent les unes des autres si l’épaisseur augmente.
Si 
, on obtient
une suite continue pour .
La solution qui se présentait sous forme d’un développement en
série des valeurs discrètes de
devient une suite continue.
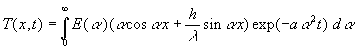
et doit vérifier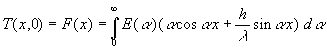
L’orthogonalisation conduit à :
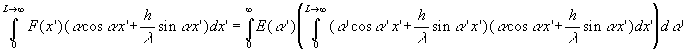
Le calcul de 
est
fastidieux et n’est pas reproduit ici.
],
il suffit de faire 
.
],
il suffit de faire 
.
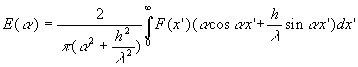
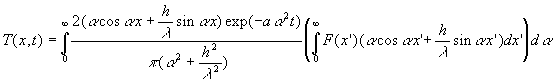
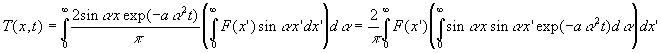
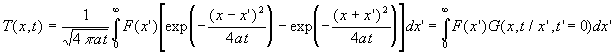
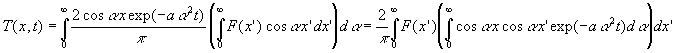
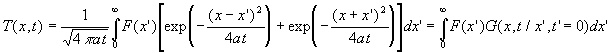
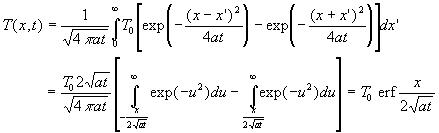
On trouvera en annexe 2 les propriétés de la fonction erf
définie par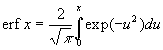 
et de erfc définie par 
.
nous
ramène à l’exemple précédent.
La solution est donc,
et
à remarquer que cette fonction est solution de 
[Exemple 1’].
Par suite, 
L’intégration se fait par partie et n’offre guère de difficultés.
En tenant compte de 
,
on obtient
et à remarquer que cette fonction est solution de 
[Exemple 1’].
Par suite, 
[équation différentielle du premier ordre avec second membre]
En tenant compte de ,
on obtient :
5.2. Milieu semi-infini de révolution ( 0 < r < ¥ )
Nous ne reproduisons pas les calculs.
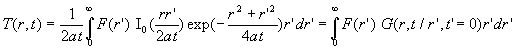
5.3. Milieu semi-infini à symétrie sphérique ( 0 < r < ¥ )
La recherche de la solution sous la forme 
conduit à : 
A ces équations, il convient d’ajouter le fait que la température
en r = 0 reste finie c’est à dire 
.
La solution pour 
correspond à celle d’un mur semi-infini soumis à une condition
de type température imposée.
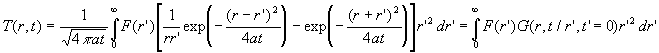
5.4. Approximation milieux semi-infinis
Il nous importe de savoir dans quelles conditions la solution obtenue
dans le cadre des milieux semi-infinis s’identifie avec celle du milieu
fini réel.
Pour illustrer ce propos, nous prenons l’exemple 1’ du paragraphe 5.1.
Un mur d’épaisseur L, initialement à température
uniforme prise comme référence, est soumis sur sa face x
= 0 à une température 
.
La solution " mur semi-infini " c’est à dire L ®
¥ est donnée par :
Cette solution est acceptable si, en x = L, la température, en première approximation, est inchangée.
ð
; 
Les solutions " milieu fini " et " milieu semi-infini " sont identifiables
dans les premiers instants de l’évolution.
Pour le cas étudié, suivant la condition limite en x = L,
la constante de temps évolue de 
à 
.
Il est intéressant de comparer temps d’identification et constante de
temps qui est caractéristique de l’échelle de temps du système.
6. Orthogonalisation dans les milieux infinis ( - ¥ < x < + ¥ )
La recherche d’une solution à variables séparées
conduit à :
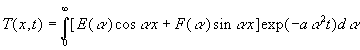avec 
Nous ne reproduisons pas les calculs. On obtient :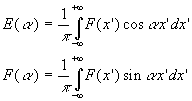 
et 
