représente
la surface de la frontière extérieure i, l’indice i
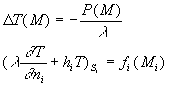
est au maximum égal à 6. CHAPITRE 2 : Les régimes permanents
Plan
1. Milieu conductif sans source interne
2. Milieu conductif sans source externe
3. Bilan thermique de type " ailette "
Il s’agit de résoudre le système d’équations linéaires(*)
:
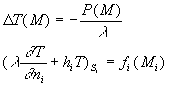
représente
la surface de la frontière extérieure i, l’indice i
est au maximum égal à 6.
(*) Pour un milieu conductif répondant à l’hypothèse de
" barre thermique ", on obtient l’équation 
. Les techniques de résolution sont transposables directement à
cette équation.
Ce système d’équations est décomposable, par superposition
rendue possible par la linéarité des équations, en
deux systèmes notés 1 et 2 :
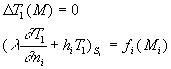système 1 |
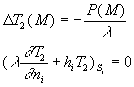système 2 |
Le champ de température est alors égal à 
Le système 1 correspond à un milieu conductif sans source
interne soumis à au moins une source externe, le système
2 correspond à un milieu conductif sans source externe soumis à
des sources internes.
1. Milieu conductif sans source interne (système 1)
1.1. Résistance thermique
1.1.1. Définition
 |
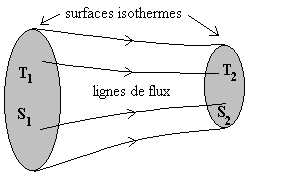On considère deux surfaces isothermes S1
et S2 de températures 
et  .
Ces deux surfaces sont correspondantes c’est à dire que toute ligne
de flux quittant la surface S1 atteint la
surface S2 . Pour un milieu conductif en régime permanent sans source interne, le bilan thermique s’écrit  . |
Appliquons, sur le volume fermé délimité par les
deux surfaces isothermes S1 et S2
et la surface latérale constituée de toutes les lignes de
flux s’appuyant sur le contour fermé délimitant les deux
surfaces isothermes, le théorème d’Ostrogradsky,
Entre surfaces isothermes correspondantes le flux de chaleur est conservé.
Pour une surface isotherme quelconque S du tube de courant 
Le calcul de la circulation de 
suivant une ligne de flux quelconque joignant les surfaces isothermes S1
et S2 conduit à :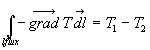 
La multiplication de 
par un coefficient quelconque entraine la multiplication par le même coefficient
de 
.
On obtient donc la relation : 
R est appelée résistance thermique, c’est l’analogue thermique de la résistance électrique. Elle est inversement proportionnelle à la conductivité du milieu et augmente avec la longueur des lignes de flux.
112 Résistances thermiques en série, en parallèle
| Tubes de flux de chaleur en série
Les surfaces isothermes S1 S2
d’une part, S2 S3
d’autre part se correspondent, leurs températures respectives sont Par suite |
Tubes de flux de chaleur en parallèle
|
1.1.3. Résistance thermique relative à un coefficient d’échange h
ð
Remarque : on retrouve les relations classiques de l’électrocinétique des courants continus sur l’association de résistances.
1.2. Les problèmes monodimensionnels
1.2.1. Le mur
En Thermique, on appelle " mur " un milieu dont les évolutions de température dépendent de la seule variable cartésienne x (les gradients dans tout plan perpendiculaire à l’axe Ox sont nuls).
 |
ð
|
 |
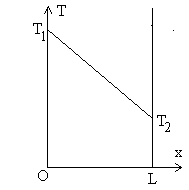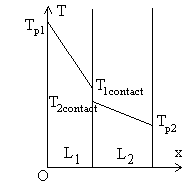Un bilan thermique entre deux sections quelconques
prises dans chacun des deux murs conduit à :
 puisque
les sections transversales ont même surface. Par suite,  ; 
Le problème posé est celui de l’écart |
L’extrapolation jusqu’au contact du champ de température dans le milieu
1 conduit à la valeur 
qui est différente de 
température
d’extrapolation jusqu’au contact dans le milieu 2 si la couche de transition
est notable c’est à dire s’il existe un phénomène de constriction
entrainant un allongement des lignes de flux.
Ceci explique l’introduction d’une résistance thermique supplémentaire
appelée résistance thermique de contact puisque la
résistance thermique augmente avec la longueur des lignes de flux.
 |
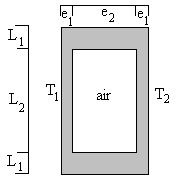La dimension transversale de la brique est égale
à H.
Dans la cavité d’air, coexistent, en parallèle, des échanges par rayonnement et par conduction si on considère que les dimensions sont suffisamment faibles pour empêcher les mouvements convectifs. La résistance pour la cavité d’air est égale à :  La résistance pour la partie centrale sera :  |
La résistance pour les " parties pleines " est égale à
: 
Ces deux résistances sont en parallèle si bien que la
résistance globale de la brique sera :
en introduisant
une conductivité équivalente 
pour le matériau composite considéré alors comme un matériau
conductif homogéne.
Application numérique :
 |
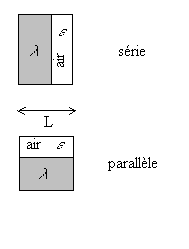Les transferts série ou parallèle
sont mal définis.
On appelle e la porosité c’est à dire la proportion en volume des cavités. Pour le schéma série,  Pour le schéma parallèle,  Généralement, on considère qu’il y a autant de schémas séries et parallèles  |
1.2.2. Symétrie de révolution autour d’un axe
; 
où r est la distance à l’axe et L une longueur axiale
arbitraire.
et 
.
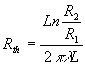représente
la résistance thermique (
).
1.2.3 Symétrie sphèrique
; 
où r est la distance au centre de symétrie.
et 
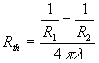représente
la résistance thermique ().
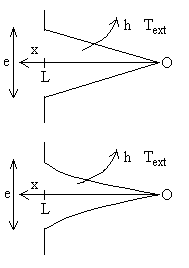
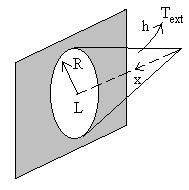
1.2.4. Milieu semi-infini
 |
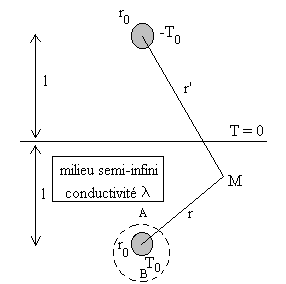La surface du milieu semi-infini est supposée
isotherme, sa température est prise comme température de
référence.
Sur la figure le milieu semi-infini s’étend vers le bas, à une profondeur l existe une canalisation de grande longueur L, de rayon r0 et de température T0 . Pour trouver le champ de température en un point M, on associe, vers le haut, un milieu semi-infini identique dans lequel on place une canalisation identique à température -T0 . L’application des solutions du paragraphe 1.2.3. donne :  . |
Les surfaces isothermes sont données par r’/r = Cste ð
cylindres de longueur L (cercles dans le plan de la figure).
D’autre part r = r’ ð plan médiateur
tel que T = 0 .
L’application de cet exercice est le cas d’une canalisation enterrée.
L’hypothèse d’un sol isotherme est discutable, aussi il convient
que la chute de température à partir de la canalisation soit
suffisante ce qui implique l >> r0
.
Sur la canalisation, on aura r = r0 , 
et 
.
Pour apprécier la validité du calcul, nous envisageons un rapport 
et calculons l’isotherme 
.
ð
La résistance thermique est égale à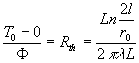 
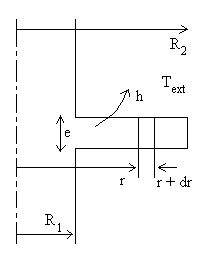
Quand le transfert thermique entre une surface et un fluide est faible,
on place sur celle-la des ailettes conductrices pour augmenter les échanges.
Ces ailettes qui pénètrent dans le fluide dans une direction
Ox sur une profondeur L peuvent être à section uniforme
ou non.
L’approximation dite de la " barre " consiste à dire
que le gradient de température est essentiellement dans une direction
Ox c’est à dire que dans une section x = Cste le champ de
température est, en première approximation, uniforme. Toutefois,
et contrairement à l’hypothèse de " mur thermique ", on ne
néglige pas les échanges de chaleur dans les directions transversales,
on en tient compte par l’intermédiaire d’un coefficient h
traduisant les échanges par convection et rayonnement.
 |
On considére un mur en contact avec un
fluide.
 ð
|
 |
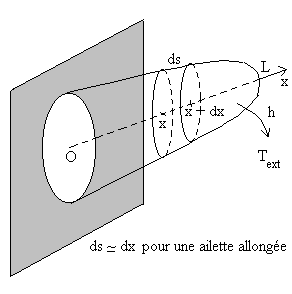Le bilan thermique entre la section x
et la section x + dx conduit à :
|
 |
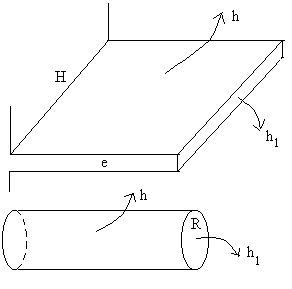Pour la section rectangulaire,
 Pour la section circulaire,  Le système d’équations à résoudre s’écrit : 
La solution est si
|
Le flux de chaleur évacué par l’ailette peut être
calculé de deux manières :
- en calculant le flux de chaleur du aux coefficients d’échanges
suivant les éléments de surface en contact avec l’extérieur,
- en calculant (plus agréable) le flux de chaleur entrant par
conduction dans l’ailette.
Pour une ailette très longue (semi-infinie), on obtient
:
(le lecteur
reprendra la résolution avec 
ou fera tendre L vers l’infini dans les résultats de l’ailette
finie ; dans ce dernier cas, il obtiendra la condition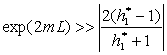 
).
La surface sans ailette, supposée à température 
et échangeant avec l’extérieur par un coefficient h, évacue
un flux de chaleur 
.
On appelle efficacité e
d’une ailette le rapport du flux de chaleur évacué par l’ailette
au flux de chaleur évacué par la surface sans ailette.
Pour l’ailette semi-infinie 
Une ailette sera performante si sa conductivité est élevée
et son épaisseur (ou son rayon) faible.
Pour une ailette de longueur finie, remarquerons que la température
se rapproche de celle extérieure lorsqu’on s’approche de l’extrémité
x = L . De plus la surface d’échange à l’extrémité
(eH) est plus faible que celle latérale (2LH) si bien qu’il
est tout à fait raisonable de négliger les échanges à
l’extrémité (mathématiquement faire 
).
On obtient 
L’ailette de longueur finie se comporte comme celle infinie si 
.
 |
La profondeur des ailettes est égale à  .
Pour l’ailette à profil triangulaire, 
et  ð .
Pour l’ailette à profil parabolique, |
- Le champ de température et le flux de chaleur évacué de l’ailette à profil triangulaire sont respectivement égaux à
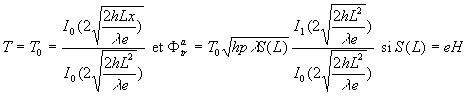
où 
sont les fonctions de Bessel modifiées de 1ère
espèce d’ordre zéro et un.
- Le champ de température et le flux de chaleur évacué par l’ailette à profil parabolique sont respectivement égaux à
 |
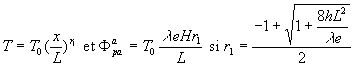
Pour cette ailette  .
Le bilan thermique conduit à :  Les conditions aux limites s’écrivent : 
La résolution donne
|
Le flux de chaleur évacué par cette ailette sera :
où 
sont les fonctions de Bessel modifiées de 2ème
espèce d’ordre zéro et un.
 |
Le bilan thermique conduit à : 
Les conditions aux limites s’écrivent :
|
La solution est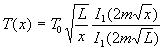 
.
Le flux de chaleur évacué par cette ailette s’écrit :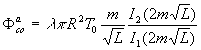 
1.3. Les problèmes pluridimensionnels
Nous avons à résoudre le système 1 d’équations
où le champ de température dépend de plusieurs variables
d’espace.
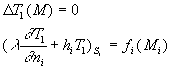
La linéarité des équations permet de chercher une
solution sous la forme,
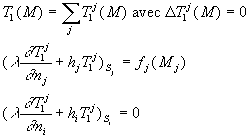avec 
;
on rappelle que i est, au maximum, égal à 6
La résolution sera faite par la technique de séparation de variables avec développement en série de fonctions orthogonales. Nous présentons cette méthode à partir d’un exemple.
 |
|
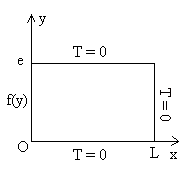Le report dans l’équation aux dérivées partielles conduit
à 
en tenant compte du fait que le premier terme ne dépend que de x
et que le second ne dépend que de y.
Les trois dernières équations aux limites pour lesquelles le second
membre est nul s’écrivent 
puisqu’elles doivent être vérifiées quelque soit y
ou quelque soit x.
Par intégration on obtient :
* 
qui,
après application des conditions aux limites, devient
(les valeurs possibles 
conduisent à la même solution et ne sont donc pas à considérer)
* 
en tenant
compte de la condition aux limites 
.
La condition aux limites (sauf cas particulier) 
n’est pas assurée pour une valeur particulière de 
.
Dans un deuxième temps, on remarque que, le système
d’équations étant linéaire, on peut chercher une solution
sous la forme d’une combinaison linéaire.
où tous
les sont
possibles.
Cette combinaison est connue sous le nom de développement
en série de Fourier.
La dernière condition aux limites à vérifier s’écrit
alors :
Le dernier temps consiste à déterminer les coefficients 
par la méthode des fonctions orthogonales.
Pour cela, nous multiplions chacun des membres par 
et intégrons sur l’intervalle de variation de y. La variable d’intégration
étant " muette ", nous l’appelerons y’ plutôt que y
qui est attribuée, dans l’exemple, à une variable cartésienne
d’espace.
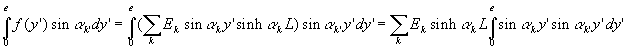
Le lecteur vérifiera sans peine que, dans notre exemple,
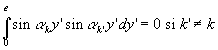, que 
et qu’en conséquence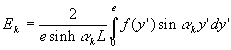 
Le champ de température s’écrit alors :
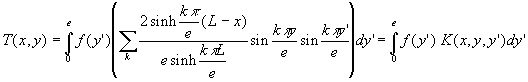
1.3.2. Quelques remarques et conséquences générales
est dite homogène.
est dite non-homogène.
est tel que l’on doit être conduit à une infinité de valeurs 
positives, appelées valeurs propres qui vont permettre un développement
en série de Fourier. L’équation qui permet de trouver les valeurs
est appelée équation transcendante.Soit l’équation différentielle 
avec
les conditions aux limites 
et 
L’équation transcendante détermine une infinité de valeurs
et la solution u est traitée comme une fonction de x et
de.
est solution
de 
est solution
de 
où
nous considérons deux valeurs quelconques possibles de 
qui sont identiques si 
et différentes si 
.
En multipliant respectivement par 
et 
ces
deux dernières équations, en retranchant les deux équations
obtenues et en intégrant sur l’intervalle 
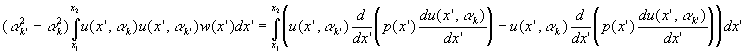
En intégrant par partie, on obtient
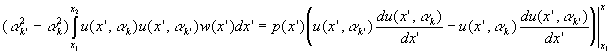
Le membre de droite s’annule pour les cas particuliers :
ou pour
des conditions aux limites homogènes :
et 
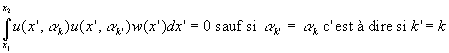
On dit que les fonctions propres u sont orthogonales sur l’intervalle
suivant la fonction de pondération 
.
.
Ainsi, dans l’exemple étudié, 
ð
Remarquons que 
a
été obtenu à partir de 
.
Si, par la méthode du bilan thermique, on cherche à établir
l’équation 
,
il convient de définir un élément de volume 
où
S peut être pris arbitrairement égal à 1.
L’identification 
conduit pareillement à 
.
Dans les problèmes à symétrie de révolution,
on traite l’équation différentielle
ï
ð
ð
Pour établir l’équation différentielle 
,
il convient de définir un élément de volume 
où 
peuvent être pris égaux à 1 (souvent, on fait 
).
L’identification 
conduit à 
.
1.3.4 Cas d’une direction homogène avec des conditions aux limites de 2ème espèce
L’exemple du paragraphe 1.3.1. est repris et modifié en ce qui
concerne les conditions aux limites suivant la direction y.
; 
; 
conduit à 
Par intégration, on obtient :
* 
qui,
après application des conditions aux limites [
]
devient 
avec 
et 
* 
en tenant
compte de 
La différence avec l’exemple du paragraphe 1.3.1. est la possibilité
k = 0 qui entraine 
.
Pour , les
équations différentielles, après séparation des
variables, s’écrivent 
et 
.
Compte tenu des conditions aux limites, on obtient 
.
Le développement en série de Fourier devient :
Il doit vérifier 
ce qui implique 
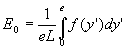et 
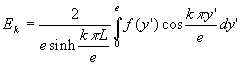
La solution s’écrit :
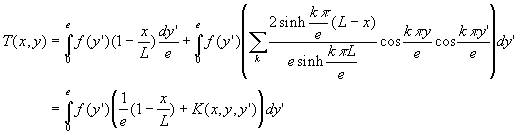
1.3.5. Des exemples pour se perfectionner
1.3.5.1. Champ de température avec une condition de 3ème espèce
; 
; 
; 
La méthode est identique à celle suivie lors de l’exemple
du paragraphe 1.3.1.
On obtient 
et, après application de la condition aux limites en 
, 
.
La condition en y = e conduit à l’équation transcendante 
.
est inchangé.
Par suite, 
,
les coefficients 
sont calculés pour vérifier 
ce qui entraine 
.
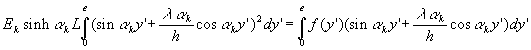La suite est une question de calcul.
En fait dans le cas présent, il était intéressant d’utiliser 
et d’écrire 
.
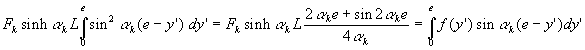
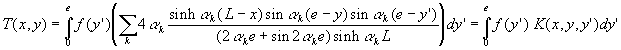
Remarque : une série de ce type est appelée
série de Fourier si les coefficients 
sont
équidistants les uns des autres; la série ci-dessus n’est
pas une série de Fourier, elle se traite cependant de manière
analogue
1.3.5.2. Champ de température
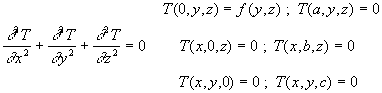
Les directions y et z sont homogènes.
ð
L’écriture des conditions aux limites conduit à :
* 
; 
; 
* 
* 
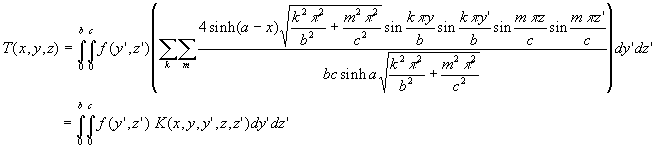
La méthode est généralisable à n variables sans difficulté particulière.
1.3.5.3. Champ de température à symétrie de révolution 
; 
; 
Remarque : nous avons écrit que la température
reste finie sur l’axe de révolution, on montre que la condition
flux de chaleur nul est équivalente.
La séparation de variables 
conduit aux équations différentielles 
et 
Après intégration et application des conditions aux limites 
où
La fonction 
est la fonction de Bessel modifiée de première espèce d’ordre
0, la fonction de Bessel modifiée de deuxième espèce d’ordre
0 
n’apparait
pas dans la solution car elle devient infinie pour r = 0 (on se rapportera
à l’annexe 1 sur les fonctions de Bessel).
ð
; 
; 
La séparation de variables 
conduit aux équations différentielles 
et 
Après intégration et application des conditions aux limites 
où 
est l’équation transcendante.
La fonction 
est la fonction de Bessel de première espèce d’ordre 0, la fonction
de Bessel de deuxième espèce d’ordre 0 
n’apparait pas dans la solution car elle devient infinie pour r = 0 (on
se rapportera à l’annexe 1 sur les fonctions de Bessel).
ð
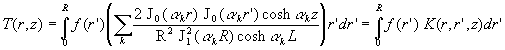
1.3.5.4. Champ de température à coordonnées cylindriques
Pour cette équation aux dérivées partielles, les valeurs caractéristiques sont toujours fournies par la " direction j ".
La séparation de variables 
conduit à :
ð
ð
L’étude des conditions aux limites de j est singulière.
1)
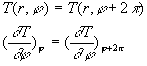ð
2)
L’écriture d’une condition de type 
n’est pas possible à cause du terme r qui ne s’élimine
pas.
Les seules conditions possibles sont celles de première ou de deuxième
espèce 
et/ou 
.
Le cas 
est possible si les deux conditions aux limites sont de deuxième espèce.
On est, encore, conduit à 
.
Le cas particulier du cylindre plein (r = 0) conduit à
B = 0 c’est à dire à 
Pour illustrer ces propos, on considère deux exemples
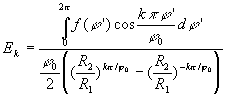
ð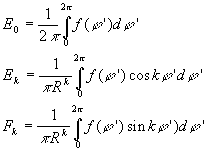
; 
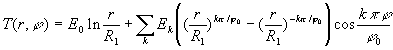
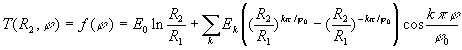
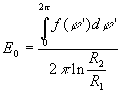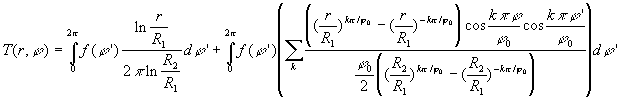
1.3.5.6. Champ de température à coordonnées cylindriques
La séparation de variables 
conduit
à
ð
On retrouve la discussion du paragraphe précédent sur la direction
j , la direction z doit être
homogène [
]
pour fournir la suite de valeurs .
où 
sont les fonctions de Bessel modifiées d’ordre n
de première espèce et de deuxième espèce.
Remarques :
* 
* 
doit
être considéré pour 
Il n’est pas donné d’exemple.
1.3.5.7. Champ de température à coordonnées sphériques 
Pour cette équation aux dérivées partielles, les valeurs
caractéristiques sont toujours fournies par la " direction q
". La séparation de variables 
conduit à :
Le traitement mathématique présente quelques particularités.
On pose 
et on fait le changement de variables 
pour obtenir :
ð
où 
sont les polynomes de Legendre d’ordre n de première espèce et
de seconde espèce (le lecteur se reportera à l’annexe sur les
polynomes de Legendre).
ð
Les valeurs à considérer pour n sont 
[
est possible
puisque 
,
cependant l’écriture générale de g reste valide
pour ] .
si bien que,
dans tout problème où 
sont inclus, le coefficient B est nul et le polynome 
n’apparait pas dans les solutions.
En fait, nous limitons nos propos à 
et utilisons les propriétés 
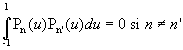et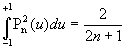 
.
Avec quelques complications, il est possible d’envisager d’autres intervalles
de variation pour q
Pour les conditions précisées, 
Exemple :
ð
ð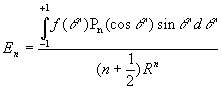
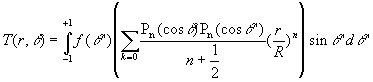
1.3.5.8 Champ de température à coordonnées sphériques 
La résolution de ce type de problème qui fait apparaitre les Polynômes associés de Legendre n’est pas envisagée dans cet ouvrage.
1.3.6. Remarques
En Conduction de la Chaleur, les fonctions propres nécessaires
sont :
- les fonctions trigonométriques cosinus ou sinus (ou combinaison
linéaire), les variables sont soient les variables cartésiennes
soit la distance à un point dans le cas de la symétrie sphérique,
la fonction w est égal à 1,
- les fonctions de Bessel dans le cas de la symétrie de révolution
et la fonction w est égal à r distance à
l’axe,
- les polynomes de Legendre dans le cas des coordonnées sphériques
et la fonction w est égal à 1, la variable étant 
.
1.3.7. Equation type " ailette " à deux dimensions
Nous reprenons l’exemple de l’ailette à section rectangulaire.
Nous admettons que cette ailette répond à l’hypothèse
de " barre " dans son épaisseur e et que cette hypothèse
n’est pas valide dans la hauteur H que nous prenons comme direction
y .
La méthode du bilan thermique conduit à l’équation
aux dérivées partielles,
Compte tenu d’un choix de l’axe y " central ", les conditions
aux limites s’écrivent :
* 
en se
limitant à une ailette semi-infinie,
* 
en supposant
H suffisamment grand.
La solution recherchée sous la forme 
conduit
à 
.
Après intégration et en tenant compte des conditions aux
limites, on obtient :
; 
soit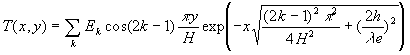 
A partir de 
,
on calcule le coefficient 
.
Le champ de température s’écrit :
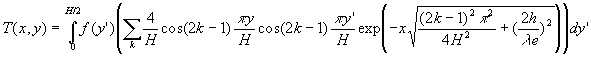
Le cas particulier courant 
conduit à :
|
|
 |
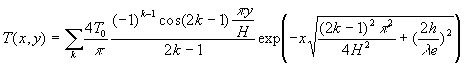
Applications de la fonction de Dirac aux sources
instantanées ou localisées
 produit
par unité de volume une quantité de chaleur Q au temps  .
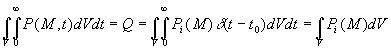
ð
ð
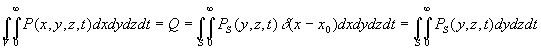
ð  )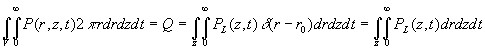
ð )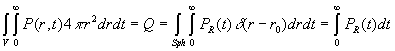
ð |
|
2. Milieu conductif sans source externe (système 2)
Nous avons à résoudre le système 2 d’équations
: 
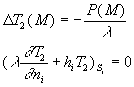
Contrairement au cas des milieux conductifs sans source interne, la
notion de résistance thermique n’est plus valide puisque le flux
de chaleur n’est pas conservatif. Chaque problème est particulier
du point de vue thermique.
Au niveau des résolutions mathématiques la technique
de séparation de variables avec développement en série
de fonctions orthogonales est performante.
Cependant nous allons voir qu’il est possible d’appliquer deux méthodologies,
- transformation du système 2 en système 1
- ou utilisation des fonctions de Green.
2.1. Transformation du système 2 en système 1
Nous cherchons une solution pour le système 2 sous la forme 
où 
est
une solution particulière du système 2
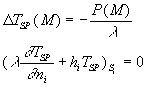ð
ð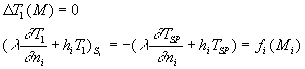
est solution
d’un système de type 1.
2.2. Méthode générale des fonctions de Green
Soit le système auxiliaire 2a associé au système 2 :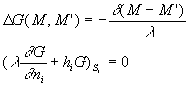 
est la fonction
de Green du problème [on montre que 
]
.
est la fonction
de Dirac.
La linéarité des équations permet d’écrire
:
ð
ð
Par suite 
2.3. Exemple
 |
|
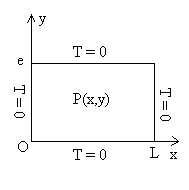2.3.1. Résolution par la méthode des fonctions de Green
On pose le système auxiliaire 2a
; 
Dans un premier temps, la methode consiste à chercher une solution
à variables séparées, c’est à dire sous la
forme 
.
Le report dans l’équation aux dérivées partielles conduit
à 
.
Cette fois, les directions x et y sont homogènes et doivent
être traitées de manière équivalente si bien que 
.
Après intégration et en tenant compte des conditions aux
limites, on obtient
Le deuxième temps consiste à chercher la fonction de Dirac
suivant un développement en série de Fourier des fonctions orthogonales,
soit 
et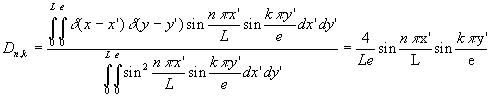 
Le report dans l’équation différentielle ð
et la fonction de Green
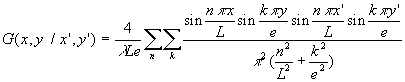
Le troisième temps consiste à calculer 
Dans le cas particulier
,
le lecteur vérifiera sans peine que
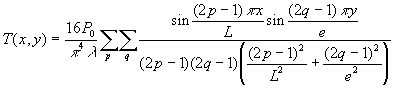
2.3.2. Résolution par transformation du système 2 en système 1
Cette méthode nécessite la connaissance d’une solution particulière.
Elle n’est donc pas envisageable si la fonction 
n’est pas exprimée explicitement. Sa portée est moins générale
que la méthode avec les fonctions de Green, cependant nous l’employons
chaque fois qu’elle est possible.
Prenons le cas particulier.
Une solution particulière est 
qui conduit au système 1 :
; 
; 
Suivant la direction y, les deux conditions aux limites sont non-homogènes.
Cependant la symétrie du problème permet d' écrire 
et seule une condition aux limites n’est pas homogène.
La recherche de la solution sous la forme 
conduit à 
et à 
.
Après intégration, en tenant compte des conditions aux
limites et en développant en série, on obtient
L’orthogonalisation à partir de 
conduit à
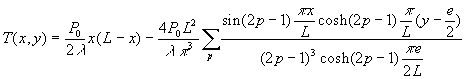
Remarque : cette solution est identique à celle trouvée par la méthode des fonctions de Green.
2.4. Quelques exemples pour se perfectionner
2.4.1. Les problèmes monodimensionnels
En fait, il s’agit de trouver la solution d’un équation différentielle.
On comprendra, à travers l’exemple ci-après, en quoi l’utilisation
d’une fonction de Green est " excessive " sur un cas aussi élémentaire.
Soit, 
dont
la solution 
est immédiate.
Par la méthode de la fonction de Green associée, on écrit
:
ð
Après intégration, en tenant compte des conditions aux
limites et en développant en série,
ð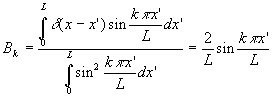
soit 
et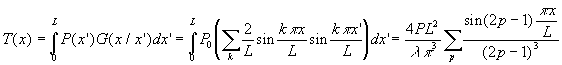 
Remarque : on démontre que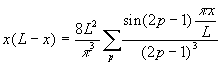 
2.4.2. Cas où l’une des dimensions est infinie
 |
|
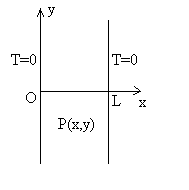La direction x est homogène ð
et 
Nous avons vu que 
.
En reportant dans l’équation aux dérivées partielles
pour G , on obtient :
Nous avons un problème de puissance localisée en y’
= y qui nous transformons en un problème de flux imposé
au même endroit.
Par commodité, on fait le changement de variable u = y -
y’ et, par raison de symétrie, on considère l’espace
u > 0 .
On obtient le système d’équations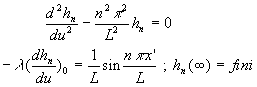 
En intégrant et en remplaçant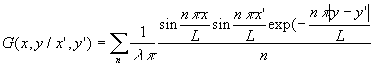 
et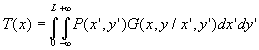 
Dans le cas particulier
,
le lecteur vérifiera que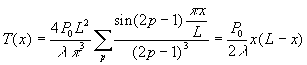 
Ce dernier résultat obtenu pour une puissance uniforme est significatif de l’importance de l’analyse pour simplifier au mieux un problème.
3. Bilan thermique de type " ailette "
Il s’agit de résoudre le système d’équations linéaires
: 
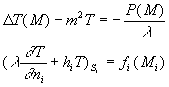
représente
la surface de la frontière extérieure i, l’indice i
est au maximum égal à 4.
Ce système d’équations est décomposable, par superposition
rendue possible par la linéarité des équations, en
deux systèmes notés 1’ et 2’ :
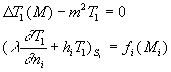 système
1’ |
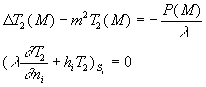système 2’ |
Le champ de température est alors égal à
Dans l’exemple du paragraphe 1.3.4. nous avons pu constater que
le système 1’ se traite suivant la même méthodologie
que le système 1.
En ce qui concerne le système 2’, la première méthodologie
consiste à le transformer en un système 1’ à l’aide
d’une solution particulière ; la deuxième méthode
plus générale consiste à appliquer la méthode
des fonctions de Green .
Nous introduisons le problème auxiliaire 3’a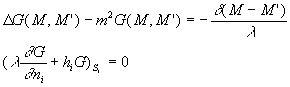 
La linéarité des équations permet d’écrire 
ð
ð
Par suite, 
.
est
la somme des résistances de chacun des milieux. 
Les surfaces isothermes
S1 S2
d’une part, S’1 S’2
d’autre part se correspondent, leurs températures respectives sont 
pour S1 et S’1
, 
pour S2 et S’2
. 
est
égale à la somme des inverses des résistances de
chacun des milieux.
et 
.
représente
la résistance thermique pour une section transversale S
et 
le flux de chaleur.
.
ð
sont respectivement
la section et le périmètre en x. 
.
:
et 
ð
.
.
pour le
champ de température.
.
dim[
= Energie/Volume]
dim[
] =
Puissance
)
dim[
] =
Puissance/Surface] 
dim[
] =
Puissance/Longueur
dim[
] =
Puissance
; 
