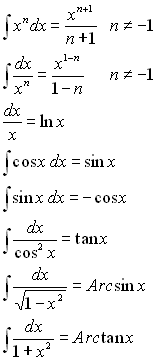
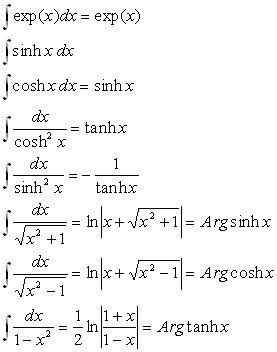
Méthodes d'intégration
Plan
1. Primitives usuelles
2. Méthodes d'intégration
2.1. Méthode immédiate
2.2. Intégration par changement de variable
2.3. Intégration par parties
3. Intégration des fonctions trigonométriques
3.1. Méthode générale
3.2. Autres méthodes
4. Intégration des fonctions rationnelles de exp(ax)
|
|
|
|
Il existe trois méthodes
2.1.1. La fonction à intégrer se trouve dans le tableau des primitives usuelles
2.1.2. La fonction à intégrer se ramène au tableau des primitives usuelles
Exemple : 
2.2. Intégration par changement de variable
On pose 
soit 
- Exemple 1 : 
On pose 
soit
- Exemple 2 : 
On écrit
sous la forme
Cas 
On pose 
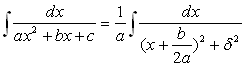
Le changement de variable 
conduit à : 
Cas
On pose
Le changement de variable 
conduit à :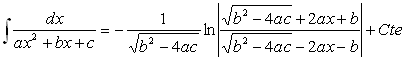 
Cas
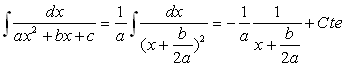
ð 
Exemple : 
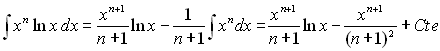
Dans certains cas, il faut répéter plusieurs fois cette opération
Exemples : 
ou 
Cas des formules de récurrence
Exemple : 
; 
; 
3. Intégration des fonctions trigonométriques
On fait le changement de variable 
ð 
ð 
Exemple :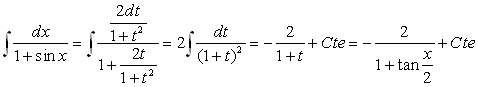 
3.2.1. 
ne change pas de signe quand on change 
On fait le changement de variable 
ð 
ð 
3.2.2.
ne change pas de signe quand on change 
On fait le changement de variable 
ð 
ð 
3.2.3.
ne change pas de signe quand on change 
On fait le changement de variable 
ð 
ð 
3.2.4. Utilisation des formules d'Euler
3.2.5. Utilisation de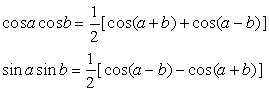 
Exemple : 
4. Intégration des fonctions rationnelles de exp(ax)
On fait le changement de variable 
ð 
ð 
