Exercices de Thermodynamique avec des gaz parfaits
Méthodologie commune aux exercices ci-après
1 – On considère un gaz parfait pour lequel ![]() .
.
1) Calculer l'énergie interne U et l'entropie S. On exprimera S avec les trois couples de variables (T, V), (T, p) et (p, V).
2) Comment sont affectés les résultats des questions
1) et 2) si ![]() dépend
de la température.
dépend
de la température.
3)a) Montrer que dans le cas d’une transformation réversible
isotherme à la température ![]() de la pression
de la pression ![]() à la pression
à la pression ![]() ,
on peut calculer les quantités de travail et de chaleur échangées
par le gaz parfait par deux méthodes différentes.
,
on peut calculer les quantités de travail et de chaleur échangées
par le gaz parfait par deux méthodes différentes.
3)b) Comment pourrait-on calculer l’entropie créée ![]() dans le cas d’une transformation isotherme irréversible à température
dans le cas d’une transformation isotherme irréversible à température
![]() , la pression
, la pression
![]() étant
appliquée brutalement sur la face extérieure du piston.
étant
appliquée brutalement sur la face extérieure du piston.
3)c) Comparer travail de compression isotherme réversible et irréversible.
Comparer travail de détente isotherme réversible et irréversible.
On pourra prendre à titre d'exemple ![]()
| Réponse 1 | Réponse 2 | Réponse 3a | Réponse 3b | Réponse 3c |
2 - Une masse d’air (assimilé à un gaz
parfait) ![]() occupe
un volume
occupe
un volume ![]() la
pression atmosphérique
la
pression atmosphérique ![]() et à la température
et à la température ![]() .
On la comprime par une opération réversible jusqu’à une
pression
.
On la comprime par une opération réversible jusqu’à une
pression ![]() .
.
1) En supposant que, pendant cette compression, la température du gaz soit maintenue constante, calculer le travail échangé pour effectuer la compression. Calculer la variation d’énergie interne et la quantité de chaleur échangée pendant cette compression.
2) En supposant que la compression soit faite de manière adiabatique, calculer le volume final et la température finale de l’air. Calculer le travail échangé, montrer qu’il s’exprime en fonction des températures finale et initiale. Retrouver ce résultat par la considération de l’énergie interne.
3) On comprime adiabatiquement le gaz, en partant du même
état initial, jusqu’à une pression p’ , puis on le laisse
refroidir sans changer son volume jusqu’à la température ambiante
![]() . On veut, après
refroidissement, obtenir de l’air à la pression
. On veut, après
refroidissement, obtenir de l’air à la pression ![]() .
.
Calculer la pression p’ , le travail échangé au cours de
la compression adiabatique, ainsi que la chaleur échangée pendant
le refroidissement.
A.N. ![]()
| Réponse 1 | Réponse 2 | Réponse 3 |
3 - On considère une mole de gaz parfait diatomique
initialement dans l’état 0 (![]() ;
;![]() ;
; ![]() ).
).
On amène ce gaz dans l’état 1 (![]() ;
;![]() ;
; ![]() ) de deux manières
différentes :
) de deux manières
différentes :
a / par compression adiabatique réversible,
b / par compression isotherme réversible jusqu’à
la pression ![]() puis
échauffement à pression constante jusqu’à la température
puis
échauffement à pression constante jusqu’à la température
![]() .
.
1) Représenter les évolutions a / et b / sur un diagramme (p en ordonnées, V en abscisse)
2) Calculer les travaux ![]() et les quantités de chaleur
et les quantités de chaleur ![]() au cours de chacune des évolutions. Conclusions.
au cours de chacune des évolutions. Conclusions.
| Réponse 1 | Réponse 2a | Réponse 2b |
4 - On dispose dans un cylindre fermé par un
piston une certaine masse d’un gaz parfait diatomique (![]() ).
Les parois du cylindre et du piston sont isolées et supposées
imperméables à la chaleur. Dans les conditions initiales, le volume
occupé par le gaz est
).
Les parois du cylindre et du piston sont isolées et supposées
imperméables à la chaleur. Dans les conditions initiales, le volume
occupé par le gaz est ![]() ,
la pression est
,
la pression est ![]() et la température
et la température ![]() .
.
1) Calculer la capacité calorifique ![]() relative à cette masse de gaz.
relative à cette masse de gaz.
2) On comprime ce gaz de manière réversible jusqu’à
![]() .
.
2)1) Dans quelle(s) condition(s) la réversibilité est-elle réalisée
?
2)2) Calculer ![]() .
.
2)3) Calculer le travail ![]() au cours de l’évolution.
au cours de l’évolution.
3) On comprime maintenant le gaz en partant du même état
initial (![]() ) mais
en appliquant brutalement
) mais
en appliquant brutalement ![]() .
.
3)1) Que peut-on dire de la transformation ?
3)2) Exprimer le travail ![]() échangé par le système de deux manières différentes.
échangé par le système de deux manières différentes.
3)3) En déduire la valeur de ![]() en fin d’évolution ainsi que
en fin d’évolution ainsi que ![]() .
Comparer ces résultats à ceux de la question 2). Expliquer la
différence.
.
Comparer ces résultats à ceux de la question 2). Expliquer la
différence.
4) On suppose que l’on retire l’isolant thermique qui entourait
le cylindre, les parois deviennent perméables à la chaleur. On
réalise un refroidissement isobare de l’état (![]() )
à l’état (
)
à l’état (![]() ).
).
Calculer la quantité de chaleur échangée au cours de cette
transformation.
| Réponse 1 | Réponse 21 | Réponse 22 | Réponse 23 | Réponse 31 | Réponse 32 | Réponse 33 | Réponse 4 |
5 - Un cylindre indéformable dont les parois
sont isolées thermiques contient de l’azote (assimilé à
un gaz parfait) réparti dans deux compartiments A et B séparés
par un piston également adiabatique. Ce piston peut se mouvoir sans frottement.
Le compartiment A contient ![]() de gaz, le compartiment B contient
de gaz, le compartiment B contient ![]() de gaz.
de gaz.
Dans A, une résistance électrique de capacité calorifique
négligeable permet de chauffer le gaz. La transformation subie par le
gaz du compartiment B sera considérée comme réversible.
1) Initialement, la température ![]() et la pression
et la pression ![]() sont les mêmes dans les deux compartiments. Calculer le volume V
du cylindre.
sont les mêmes dans les deux compartiments. Calculer le volume V
du cylindre.
2) A reçoit une quantité de chaleur Q.
Ecrire les variations d’énergie interne du système complet en
appelant ![]() la température
finale dans A et
la température
finale dans A et ![]() la température finale dans B. En déduire la pression finale p.
la température finale dans B. En déduire la pression finale p.
3) Que peut-on dire de l’évolution subie par le gaz
dans le compartiment B ?
En déduire ![]() puis
puis ![]() .
.
A.N. ![]() ;
; ![]() ;
; ![]() ;
; ![]()
| Réponse 1 | Réponse 2 | Réponse 3 |
6 - On désire refroidir une mole de gaz parfait
diatomique en lui faisant subir une suite de compressions isothermes suivies
de détentes adiabatiques. Ce gaz est contenu dans un cylindre fermé
par un piston glissant sans frottement. Initialement, le gaz est à la
température ![]() et sa pression est
et sa pression est ![]() .
.
Justifier la valeur de ![]() .
.
1) Dans une première opération on comprime le
gaz de manière isotherme réversible jusqu’à la pression
![]() puis on le détend
de manière adiabatique réversible jusqu’à
puis on le détend
de manière adiabatique réversible jusqu’à ![]() .
.
1)1) Quelle est la température ![]() en fin d’évolution adiabatique ?
en fin d’évolution adiabatique ?
1)2) Calculer la quantité de chaleur ![]() et le travail
et le travail ![]() mis en jeu au cours de l’évolution isotherme, ainsi que le travail
mis en jeu au cours de l’évolution isotherme, ainsi que le travail ![]() mis en jeu au cours de l’évolution adiabatique. En déduire le
travail total W reçu par le gaz au cours de cette première
opération.
mis en jeu au cours de l’évolution adiabatique. En déduire le
travail total W reçu par le gaz au cours de cette première
opération.
Calculer la variation d’entropie ![]() au cours de cette première opération.
au cours de cette première opération.
2) Le gaz étant dans l’état ![]() on recommence la même opération (compression isotherme réversible
jusqu’à
on recommence la même opération (compression isotherme réversible
jusqu’à ![]() ,
puis détente adiabatique réversible jusqu’à
,
puis détente adiabatique réversible jusqu’à ![]() ).
).
2)1) Donner l’expression de la température ![]() obtenue à la fin de la nième opération.
obtenue à la fin de la nième opération.
2)2) Pour quelle valeur de n le gaz atteint-il une température ![]() inférieure ou égale à 100K?
inférieure ou égale à 100K?
2)3) Calculer la variation d’entropie ![]() après n opérations.
après n opérations.
3) On suppose maintenant qu’au cours de chaque opération,
la compression isotherme et la détente adiabatique sont irréversibles
(pour cela, on soumet le piston à la pression extérieure ![]() tout au long de l’évolution isotherme puis on le lâche de façon
qu’au cours de la détente adiabatique de
tout au long de l’évolution isotherme puis on le lâche de façon
qu’au cours de la détente adiabatique de ![]() à
à ![]() la pression
appliquée soit constamment la pression atmosphérique
la pression
appliquée soit constamment la pression atmosphérique ![]() ).
).
Calculer le travail ![]() et la chaleur
et la chaleur ![]() mis en jeu au cours de la première compression isotherme. Comparer à
mis en jeu au cours de la première compression isotherme. Comparer à
![]() et
et ![]() trouvés en 1)b), expliquer la différence.
trouvés en 1)b), expliquer la différence.
Calculer la température ![]() obtenue à la fin de la première détente adiabatique ainsi
que le travail
obtenue à la fin de la première détente adiabatique ainsi
que le travail ![]() échangé par le gaz au cours de cette détente. Comparer
ces résultats à ceux obtenus quand la détente adiabatique
était réversible. Conclusions ?
échangé par le gaz au cours de cette détente. Comparer
ces résultats à ceux obtenus quand la détente adiabatique
était réversible. Conclusions ?
Calculer la variation d’entropie ![]() après
la première compression isotherme et la première détente
adiabatique. Calculer les entropies créées dans la compression
isotherme et dans la détente adiabatique.
après
la première compression isotherme et la première détente
adiabatique. Calculer les entropies créées dans la compression
isotherme et dans la détente adiabatique.
| Réponse 11 | Réponse 12 | Réponse 21 | Réponse 22 | Réponse 23 | Réponse 3 |
7 - Un cylindre de section ![]() fermé par un piston P1
de masse négligeable est
fermé par un piston P1
de masse négligeable est
|
Divisé en deux compartiments A et B au moyen d’une
paroi mobile P2
de masse négligeable pouvant se déplacer librement. |
|
et le système est en équilibre sous l’action
d’une force extérieure ![]() s’exerçant sur P1
.
s’exerçant sur P1
.
1) Calculer les volumes ![]() et
et ![]() occupés
par chaque gaz.
occupés
par chaque gaz.
2) On modifie lentement la force extérieure ![]() jusqu’à la valeur
jusqu’à la valeur ![]() .
Calculer les volumes
.
Calculer les volumes ![]() et
et ![]() occupés
par chaque gaz ainsi que la température
occupés
par chaque gaz ainsi que la température ![]() et
et ![]() . Quel est
le travail W échangé. Quels sont les travaux
. Quel est
le travail W échangé. Quels sont les travaux ![]() et
et ![]() échangés
par chaque gaz.
échangés
par chaque gaz.
3) Le système étant dans l’état initial
(![]() ,
,![]() )
on rend la paroi P2
conductrice et on réalise à nouveau une compression infiniment
lente de
)
on rend la paroi P2
conductrice et on réalise à nouveau une compression infiniment
lente de ![]() à
à
![]() .
.
Que peut-on dire des transformations subies par chaque gaz et par le système
complet ?
Quelle relation lie les paramètres température et pression p
au cours de l’évolution ?
Calculer la température d’équilibre finale ![]() ainsi que les travaux
ainsi que les travaux ![]() ,
,
![]() et W’ échangés
par chaque gaz et par le système dans son ensemble. Comparer ces résultats
à ceux en 2).
et W’ échangés
par chaque gaz et par le système dans son ensemble. Comparer ces résultats
à ceux en 2).
4) Le système étant dans l’état initial
(![]() ,
,![]() )
on pratique une ouverture dans la paroi P2
, les deux gaz se mélangent, la paroi P2
est déposée au fond du cylindre et ne joue plus aucun rôle.
On réalise alors la compression infiniment lente de
)
on pratique une ouverture dans la paroi P2
, les deux gaz se mélangent, la paroi P2
est déposée au fond du cylindre et ne joue plus aucun rôle.
On réalise alors la compression infiniment lente de ![]() à
à ![]() .
.
Que peut-on dire des deux phases successives de l’évolution ?
Que peut-on dire de la température d’équilibre finale et du travail
échangé par le système ?
| Réponse 1 | Réponse 2 | Réponse 3 | Réponse 4 |
8 - Un réservoir indéformable de volume
![]() dont les parois
sont adiabatiques est
dont les parois
sont adiabatiques est
|
Muni d’un robinet R permettant de le mettre en communication
avec l’air atmosphérique extérieur. 1) Le réservoir étant rempli d’air à
la température 2) On ouvre brusquement le robinet R de manière à
ramener la pression de l’air dans le réservoir à la valeur
de la pression atmosphérique |
|
Expliquer pourquoi on peut considérer que l’air restant
dans le réservoir s’est détendu de manière adiabatique
quasi-statique. Calculer la température ![]() et la masse
et la masse ![]() de
l’air restant dans le réservoir à la fin de cette détente.
de
l’air restant dans le réservoir à la fin de cette détente.
3) On suppose maintenant que l’on a fait le vide dans le réservoir.
On ouvre brusquement le robinet R, l’air pénètre dans le réservoir
jusqu’à ce que la pression soit égale à la pression extérieure
![]() .
.
3)1) Expliquer la nature de cette opération et donner une expression
littérale du travail W échangé au cours de l’opération
(pour cela, on considérera un système constitué de la quantité
d’air entrant dans le réservoir).
3)2) Calculer la température ![]() de l’air ainsi que le travail W.
de l’air ainsi que le travail W.
4) Le robinet R étant fermé on établit
le contact thermique entre l’intérieur et l’extérieur du réservoir
en enlevant l’isolant qui protégeait les parois. La température
de l’air passe alors de ![]() à
à ![]() . Calculer
la chaleur et le travail échangés.
. Calculer
la chaleur et le travail échangés.
| Réponse 1 | Réponse 2 | Réponse 31 | Réponse 32 | Réponse 4 |
|
9 – Un cylindre horizontal est fermé à
l’une de ses extrémités par une paroi fixe F0
et à l’autre l'extrémité par un piston qui peut coulisser
sans frottement le long du cylindre. |
|
1) Dans la situation initiale le compartiment A de volume ![]() contient un gaz parfait diatomique à température
contient un gaz parfait diatomique à température ![]() ,
le compartiment B de volume
,
le compartiment B de volume ![]() est vide.
est vide.
Calculer le nombre n de moles dans le cylindre.
2) Les parois du cylindre et le piston sont imperméables
à la chaleur et de capacités calorifiques négligeables.
On perce un orifice dans la paroi fixe F.
Le volume ![]() est
suffisamment grand pour que la pression finale soit inférieure à
est
suffisamment grand pour que la pression finale soit inférieure à
![]() .
.
2)1) En déduire, dans l’état final, le volume du compartiment
A.
2)2) Calculer par deux méthodes différentes le travail ![]() échangé avec l’extérieur par le gaz. En déduire
la température finale
échangé avec l’extérieur par le gaz. En déduire
la température finale ![]() ,
la pression finale
,
la pression finale ![]() du gaz et le volume minimal
du gaz et le volume minimal ![]() pour que la pression finale
pour que la pression finale ![]() reste inférieure à
reste inférieure à ![]() .
.
2)3) Calculer l’entropie ![]() créée. Le résultat est-il conforme au second principe de
la Thermodynamique ?
créée. Le résultat est-il conforme au second principe de
la Thermodynamique ?
3) On revient aux conditions définies en 1), les parois
du cylindre et le piston étant imperméables à la chaleur
et de capacités calorifiques négligeables.
![]() est maintenant
inférieur à
est maintenant
inférieur à ![]() et la pression finale du gaz sera
et la pression finale du gaz sera ![]() après avoir percé l’orifice.
après avoir percé l’orifice.
3)1) Calculer par deux méthodes différentes le travail ![]() échangé avec l’extérieur par le gaz. En déduire
la température finale
échangé avec l’extérieur par le gaz. En déduire
la température finale ![]() .
.
3)2) Calculer l’entropie ![]() créée.
Le résultat est-il conforme au second principe de la Thermodynamique
?
créée.
Le résultat est-il conforme au second principe de la Thermodynamique
?
4) On revient aux conditions initiales et on bloque le piston. Que se passe t’il lorsque l’on perce l’orifice ? Conclusions.
| Réponse 1 | Réponse 21 | Réponse 22 | Réponse 23 | Réponse 31 | Réponse 32 | Réponse 4 |
10 - Expérience de Clément et Desormes
Soit un ballon de volume V muni de deux tubulures, l’une terminée par un robinet, l’autre raccordée à un manomètre rempli d’un liquide de masse volumique m . On néglige le volume des tubulures.
|
A l’instant initial le ballon est rempli d’un gaz parfait à
la température ambiante 1) On suppose que la différence de pression entre
le ballon et le milieu extérieur est petite comparée à
la pression extérieure |
|
On laisse ensuite le système échangé de la chaleur avec le milieu extérieur de telle sorte que les températures dans le ballon et à l’extérieur deviennent égales.
2) Donner l’expression de la nouvelle dénivellation h’ du liquide. En déduire l’expression de g en fonction de h et h’.
A.N. ![]() ;
; ![]() ;
; ![]()
11 - On considère un récipient fermé par un piston
de masse ![]() mobile
sans
mobile
sans
|
11 - On considère un récipient fermé
par un piston de masse
|
|
1) Calculer la pression ![]() du
gaz intérieur à l’équilibre.
du
gaz intérieur à l’équilibre.
2) Le piston est déplacé de sa position d’équilibre
et lâché sans vitesse initiale. Les transformations ultérieures
sont quasi-statiques mais assez rapides pour être adiabatiques.
2)1) Décrire la nature des mouvements (de faible amplitude) du piston.
2)2) Soit z la position du piston par rapport à sa position d’équilibre.
Ecrire la variation de volume ![]() du gaz intérieur.
du gaz intérieur.
2)3) Trouver une relation entre les variations de volume ![]() et
et ![]() du gaz intérieur
(ces variations restent faibles devant respectivement V et
du gaz intérieur
(ces variations restent faibles devant respectivement V et ![]() ).
).
2)4) En déduire l’équation différentielle du mouvement
du piston. Donner l’expression théorique de la période ![]() du mouvement. Si
du mouvement. Si ![]() est la période, calculer g .
est la période, calculer g .
2)5) Que deviendraient ces résultats pour des gaz réels ?
| Réponse 1 | Réponse 21 | Réponse 22 | Réponse 23 | Réponse 24 | Réponse 25 |
12 - Un cylindre (C), indéformable d’axe horizontal
Ox, de section s, a des parois parfaitement calorifugées. Il est
séparé en deux compartiments par un piston (P), parfaitement calorifugé,
de masse m, mobile sans frottement. Les compartiments 1 et 2 contiennent
chacun une mole de gaz parfait, initialement dans l’état (![]() ).
).
On prendra 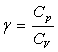 constant.
constant.
|
|
Un opérateur extérieur déplace légèrement le piston et l’abandonne sans vitesse initiale. 1) Expliquer pourquoi les transformations peuvent être prises réversibles. 2) Calculer, en première approximation, les pressions
3) Ecrire pour le piston (P) de masse m le principe fondamental de la dynamique et en déduire la période des oscillations du piston. |
On rappelle que ![]()
| Réponse 1 | Réponse 2 | Réponse 3 |
13 - La matière étudiée est un gaz parfait diatomique aux températures ordinaires.
1) Indiquer et justifier la valeur de la capacité
calorifique molaire à volume constant ![]() .
.
2) Déterminer U et S pour n moles.
3) Les transformations, qui seront supposées
réversibles, sont décrites par la relation ![]() où
où ![]() est
une constante.
est
une constante.
3)a) Montrer que, par intégration, on obtient, au cours de la
transformation, ![]()
3)b) Déterminer les valeurs de ![]() correspondant aux transformations isotherme, isobare, isochore et adiabatique.
Pour ces valeurs de
correspondant aux transformations isotherme, isobare, isochore et adiabatique.
Pour ces valeurs de ![]() ,
expliciter la relation
,
expliciter la relation ![]() .
Commentaires.
.
Commentaires.
| Réponse 1 | Réponse 2 | Réponse 3a | Réponse 3b |
14 - Dans ce problème, l’air est considéré
comme un gaz parfait constitué de deux gaz parfaits diatomiques dont
les proportions en masse sont de 21% de dioxygène ![]() de masse molaire
de masse molaire ![]() et de 79% de diazote
et de 79% de diazote ![]() de masse molaire
de masse molaire ![]() .
.
1)a) Montrer que la masse molaire de l’air est égale
à ![]() .
.
1)b) En se limitant à des conditions courantes de températures
où les variations de la capacité calorifique molaire à
pression constante avec la température sont négligeables, montrer
que ![]() quelques
soient les valeurs de
quelques
soient les valeurs de ![]() ;
en déduire la valeur de
;
en déduire la valeur de ![]() .
.
1)c) Calculer les expressions de l’énergie interne U, de
l’enthalpie H et de l’entropie S de ce gaz parfait.
2) Une mole d’air subit une transformation où
il évolue d’un état (![]() )
à un état (
)
à un état (![]() ).
).
|
|
2)a) Comparer la température
|
Représenter graphiquement la transformation 1
et en déduire que les travaux échangés ![]() sont tels que
sont tels que ![]() si
si ![]() .
.
2)c) Calculer ![]() [on montrera que, pour la transformation 2,
[on montrera que, pour la transformation 2, 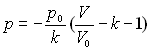 ]
à partir de l’expression du travail des forces de pression ; calculer
les quantités de chaleur échangées
]
à partir de l’expression du travail des forces de pression ; calculer
les quantités de chaleur échangées ![]() ;
montrer qu’il existe une relation simple entre
;
montrer qu’il existe une relation simple entre ![]() ;
pourquoi n’y a t’il pas de relation simple entre
;
pourquoi n’y a t’il pas de relation simple entre ![]() ?
?
2)d) Pour la transformation 2, montrer que la température
peut être écrite  ;
calculer, en fonction de
;
calculer, en fonction de ![]() ,
la température extrémale atteinte dans la transformation 2
et la nature de cet extremum.
,
la température extrémale atteinte dans la transformation 2
et la nature de cet extremum.
| Réponse 1a | Réponse 1b | Réponse 1c | Réponse 2a | Réponse 2b | Réponse 2c | Réponse 2d |