Montrer que
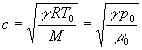 )
)A.N. Calculer, pour de l’air à température ordinaire,
Exercices de Mécanique des fluides
A) Ecoulement aérodynamique et écoulement hydrodynamique
On considère l’écoulement horizontal d’un gaz
d’une région où règne une pression ![]() (le gaz a une vitesse pratiquement nulle) à une région de pression
(le gaz a une vitesse pratiquement nulle) à une région de pression
![]() (le gaz a une
vitesse v). Cet écoulement est régi par les équations
de St Venant (écoulement aérodynamique).
(le gaz a une
vitesse v). Cet écoulement est régi par les équations
de St Venant (écoulement aérodynamique).
Montrer que ![]() si
si ![]() (on rappelle
que la vitesse du son est égale à
(on rappelle
que la vitesse du son est égale à 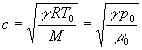 )
)
A.N. Calculer, pour de l’air à température ordinaire, ![]() pour
pour ![]() .Conclusion.
.Conclusion.
| Réponse |
B) Mesure d’un débit
Ecoulement horizontal
|
Dans une canalisation de diamètre D = 9
cm, on veut mesurer le débit d’eau. On intercale un tube
de Venturi (D = 9cm , d = 3cm). La dénivellation
du mercure dans un tube en U peut être mesurée avec précision.
On lit 4,0 mm de mercure. |
|
3) Calculer le débit d’eau, en déduire
la vitesse à l’arrivée sur le convergent.
4) A partir de la comparaison des pressions entre les points A et B,
expliquer deux applications du phénomène observé.
| Réponse 1 | Réponse 2 | Réponse 3 | Réponse 4 |
|
Ecoulement vertical |
|
C) Tube de Pitot-Prandtl ou tube de Pitot double
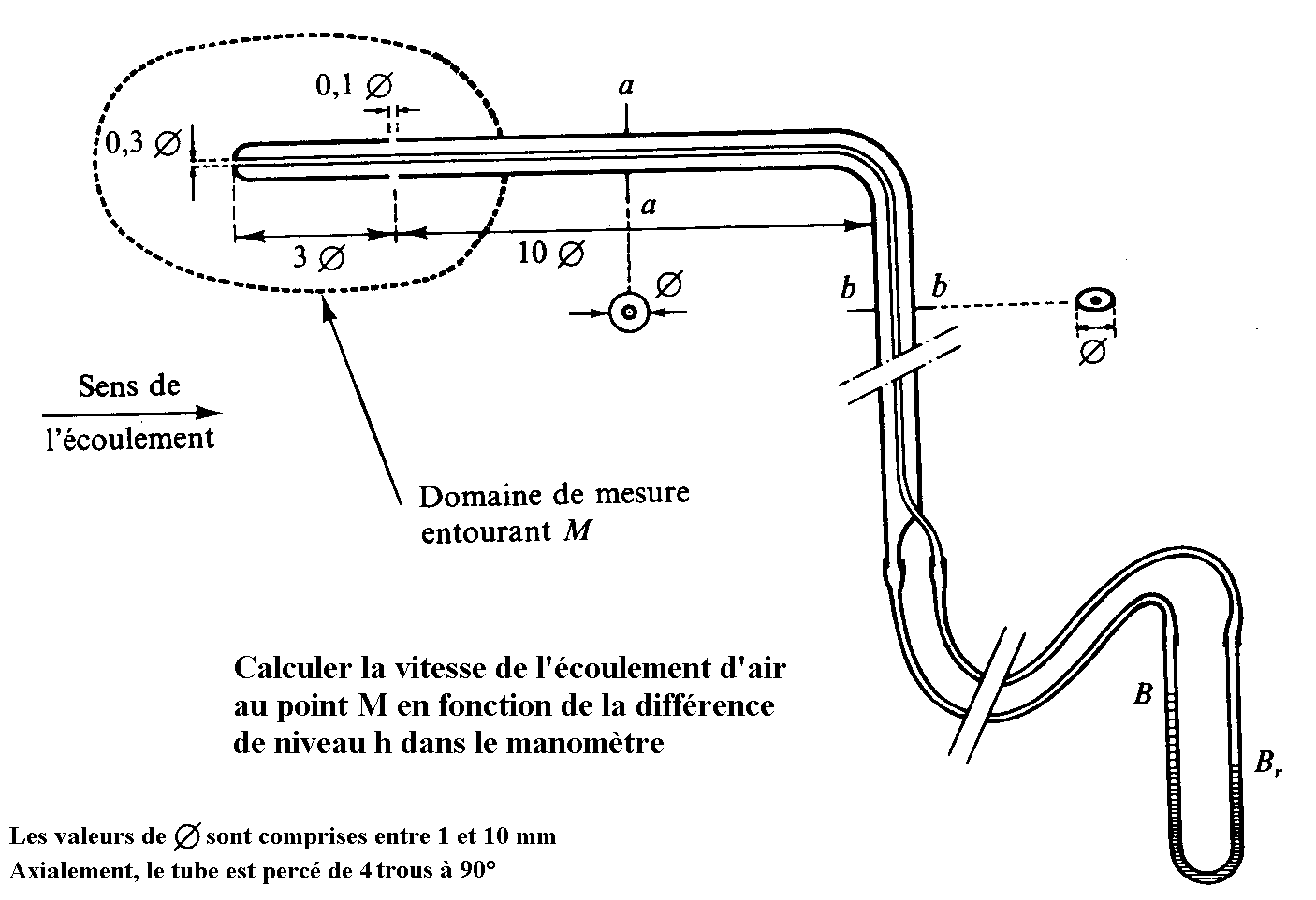
| Réponse |
D) Vidange d’un réservoir
|
Un récipient a une symétrie de révolution
autour de l’axe vertical 0z. |
|
2)1) Comparer à l’instant t , pour une
surface de l’eau de cote z toujours très supérieure à
la section s de l’orifice, vitesse v(z) du niveau d’eau à
la cote z et vitesse ![]() d’éjection.
d’éjection.
2)2) En déduire que ![]() et que l’équation différentielle donnant la hauteur d’eau est
et que l’équation différentielle donnant la hauteur d’eau est
![]() .
.
3) Le récipient a la forme d’un cylindre de révolution
de rayon ![]() . Calculer
le temps de vidange si la hauteur d’eau initiale dans le récipient est
H.
. Calculer
le temps de vidange si la hauteur d’eau initiale dans le récipient est
H.
4) Clepsydre : le rayon r du récipient
à la cote z est donné par ![]() .
.
4)1) Déterminer les coefficients n et a pour que
le niveau d’eau du récipient baisse régulièrement de 6
cm par minute.
4)2) Quelle est la hauteur minimale z = h d’eau dans le récipient
pour que ![]() .
.
4)3) Quel volume d’eau doit-on mettre dans le récipient pour que
le temps d’écoulement de l’eau entre la hauteur H et la hauteur
h soit de 15 minutes ? Quelle a pu être l’utilité
de cet appareil ?
5) Le récipient a la forme d’une sphère
de rayon ![]() . Calculer
le temps de vidange si la hauteur d’eau initiale dans le récipient est
H.
. Calculer
le temps de vidange si la hauteur d’eau initiale dans le récipient est
H.
| Réponse 1 | Réponse 21 | Réponse 22 | Réponse 3 | Réponse 41 | Réponse 42 | Réponse 43 | Réponse 5 |
E) Régimes d’écoulement dans un canal
Un canal rectiligne de grande longueur, à fond horizontal,
possède localement une section rectangulaire de largeur l, où
la profondeur d’eau est h. La vitesse d’écoulement, supposée
uniforme sur cette section droite est égale à v. Les quantités
l, h et v varient, mais sur de très grandes distances
caractéristiques, le long du canal.
L’ écoulement de l’eau, assimilée à un fluide parfait homogène
et incompressible, est stationnaire.
1) Exprimer le débit volumique
q à travers une section du canal ; que peut-on dire ?
2) Montrer que la quantité ![]() est une constante, que l’on notera
est une constante, que l’on notera ![]() ,
le long du canal.
,
le long du canal.
3) Exprimer q en fonction de ![]() .
Tracer , pour
.
Tracer , pour ![]() fixées, la courbe donnant q en fonction de h. Déterminer
la valeur maximale
fixées, la courbe donnant q en fonction de h. Déterminer
la valeur maximale ![]() de q et la hauteur
de q et la hauteur ![]() (dite critique) correspondante.
(dite critique) correspondante.
Montrer, que pour une valeur q donnée du débit inférieur
à ![]() , il
existe 2 valeurs possibles
, il
existe 2 valeurs possibles ![]() et
et ![]() de la hauteur
h, avec
de la hauteur
h, avec ![]() .
.
![]() correspond au régime " torrentiel " (faible hauteur,
grande vitesse).
correspond au régime " torrentiel " (faible hauteur,
grande vitesse).
![]() correspond au régime " fluvial " (hauteur élevée,
faible vitesse).
correspond au régime " fluvial " (hauteur élevée,
faible vitesse).
4) la largeur du canal diminue progressivement, discuter, selon le type de régime, dans quel sens se modifie h.
5) Des perturbations de la surface libre peuvent se
propager, dans le référentiel où localement l’eau est immobile,
à la célérité ![]() .
.
Etudier, selon le type de régime, si ces perturbations peuvent ou non
remonter vers l’amont, c’est à dire si la présence d’un obstacle
dans le canal a un effet sur l’écoulement en amont.
| Réponse 1 | Réponse 2 | Réponse 3 | Réponse 4 | Réponse 5 |
F) Phénomène de cavitation
|
Une conduite, de diamètre |
|
La pression atmosphérique est égale à
![]() , l’intensité
du champ de pesanteur est
, l’intensité
du champ de pesanteur est ![]() .
.
1) Montrer que si l’extrémité aval A de la conduite est
à l’air libre, on aura un phénomène de cavitation (la pression
p devient inférieure à la pression de vapeur saturante
de l’eau ![]() à
20 °C) dans une région de la conduite que l’on déterminera.
à
20 °C) dans une région de la conduite que l’on déterminera.
2) On visse à l’extrémité une tubulure de section
décroissante (injecteur), de diamètre d . Montrer que la
cavitation disparaît si ![]() ;
calculer
;
calculer ![]() .
.
3) L’injecteur a un diamètre de sortie ![]() .
Calculer la vitesse
.
Calculer la vitesse ![]() de l’eau à la sortie de l’injecteur, le débit massique
de l’eau à la sortie de l’injecteur, le débit massique ![]() et la puissance cinétique
et la puissance cinétique ![]() du jet.
du jet.
| Réponse 1 | Réponse 2 | Réponse 3 |
G) Coup de Bélier
|
Un réservoir cylindrique, d’axe vertical et de
grande section, alimente une canalisation cylindrique horizontale, de
faible section et de grande longueur l. |
|
L’écoulement de l’eau dans la canalisation est monodimensionnel
soit ![]() .
.
L’eau est assimilée à un fluide parfait incompressible de masse
volumique m.
1) Montrer que, compte
tenu des hypothèses faites, la vitesse de l’écoulement dans la
canalisation est uniforme c’est à dire que ![]() .
.
2) Si A et B sont deux points d’une même ligne de
courant (C), montrer, en intégrant l’équation d’Euler, que :
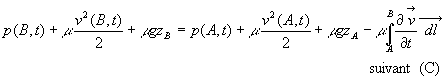
3)a) Que devient la relation précédente
si A est un point de la surface libre du réservoir et si B se
confond avec V extrémité de la canalisation.
Intégrer l’équation différentielle obtenue dans les premiers
instants après l’ouverture de la vanne en supposant que h ne varie
pratiquement pas et montrer que ![]()
A.N. : ![]() ;
;
![]() Calculer
Calculer ![]() et le temps nécessaire pour que v diffère de moins de 1%
de cette valeur.
et le temps nécessaire pour que v diffère de moins de 1%
de cette valeur.
3)b) Soit M un point d’abscisse x de la canalisation. Calculer
la pression ![]() en
appliquant la relation de la question 2) entre M et V.
en
appliquant la relation de la question 2) entre M et V.
4) La hauteur d’eau dans le réservoir est h’
et la vitesse d’écoulement de l’eau est ![]() .
.
Au temps ![]() , on
ferme la vanne, la vitesse d’écoulement varie selon
, on
ferme la vanne, la vitesse d’écoulement varie selon ![]() si T est la durée (supposée courte) de fermeture de la
vanne.
si T est la durée (supposée courte) de fermeture de la
vanne.
En appliquant la relation de la question 2) entre les points A
et M, calculer la pression ![]() .
.
Montrer que cette pression est maximale en ![]() ,
au temps
,
au temps ![]() .
.
Commenter l’application numérique pour ![]() ,
,
![]() et
et ![]() .
.
| Réponse 1 | Réponse 2 | Réponse 3a | Réponse 3b | Réponse 4 |
H) Impact d’un jet d’eau sur une plaque fixe ou mobile
Dans tout le problème, on admettra que le jet d’eau
est de vitesse v suffisamment importante pour négliger les forces
de pesanteur.
En déduire que si les trajectoires dans un liquide sont rectilignes et
parallèles, la pression dans le liquide en contact avec le milieu ambiant
est égale à ![]() pression du milieu ambiant.
pression du milieu ambiant.
Plaque plane
Sur une plaque rectangulaire homogène (largeur 2l, masse m),
on fait arriver un jet d’eau (masse volumique m.)
parallèle, horizontal de débit massique ![]() ,
de vitesse
,
de vitesse ![]() , de
section s.
, de
section s.
Après impact, on suppose que le jet se sépare en deux jets tangentiels
à la plaque, l’un vers le bas de débit massique ![]() de section
de section ![]() , l’autre
vers le haut de débit massique
, l’autre
vers le haut de débit massique ![]() de section
de section ![]() .
.
|
1) Plaque inclinée |
|
2) Plaque mobile
La plaque est libre et se déplace à vitesse ![]() .
.
L’angle a est nul et la direction centrale
du jet frappe la plaque en son centre.
2)a) Montrer que l’action du jet et de l’air environnant sur la plaque
se traduit par une force ![]() (pour établir ce résultat, on se placera dans un référentiel
lié à la plaque de vitesse
(pour établir ce résultat, on se placera dans un référentiel
lié à la plaque de vitesse ![]() par rapport au référentiel
par rapport au référentiel ![]() fixe).
fixe).
2)b) Calculer, dans ![]() ,
en fonction de
,
en fonction de ![]() :
:
Etudier l’expression de rendement ![]() en fonction de u/v.
en fonction de u/v.
|
3) Plaque courbe fixe |
|
4) Plaque courbe mobile
La plaque est maintenant à vitesse constante ![]() .
.
4)a) Exprimer les composantes de la force ![]() exercée par le liquide sur la plaque en mouvement.
exercée par le liquide sur la plaque en mouvement.
4)b) Exprimer, dans ![]() ,
la puissance
,
la puissance ![]() absorbée par la plaque en mouvement en fonction de
absorbée par la plaque en mouvement en fonction de ![]() .
En déduire le rendement du dispositif r’ , rapport de la puissance
absorbée par la plaque à la puissance incidente du jet. Etudier
ce rendement en fonction du rapport u/v.
.
En déduire le rendement du dispositif r’ , rapport de la puissance
absorbée par la plaque à la puissance incidente du jet. Etudier
ce rendement en fonction du rapport u/v.
4)c) Comment sont modifiés les résultats des questions
4)a) et 4)b) si le jet d’eau frappe une série de plaques
courbes identiques, réparties régulièrement à la
périphérie d’une roue (turbine Pelton).
| Réponse 1a | Réponse 1b | Réponse 2a | Réponse 2b | Réponse 3 | Réponse 4a | Réponse 4b | Réponse 4c |
I) Fonctionnement d’une hélice
Dans un fluide parfait, homogène et incompressible (air ou eau) de masse volumique m , est immergée une hélice. On se place dans un référentiel (R), supposé galiléen où l’hélice est animée d’un mouvement de rotation à vitesse angulaire constante autour de son axe x’x fixe

On fait les hypothèses suivantes :
1) Ecrire les deux relations entre ![]() .
.
2) Evaluer les pressions ![]() et
et ![]() en fonction
de
en fonction
de ![]() .
.
En déduire la résultante ![]() des efforts exercés par l’hélice sur le fluide en fonction de
des efforts exercés par l’hélice sur le fluide en fonction de
![]() ; discuter
le sens de
; discuter
le sens de ![]() .
.
3) Evaluer ![]() par ailleurs, en appliquant le théorème d’Euler dans (R) à
un volume de contrôle de grandes dimensions entourant l’hélice.
En déduire la relation entre
par ailleurs, en appliquant le théorème d’Euler dans (R) à
un volume de contrôle de grandes dimensions entourant l’hélice.
En déduire la relation entre ![]() .
.
4) Evaluer la puissance ![]() fournie au fluide par l’hélice, mesurée dans (R) :
fournie au fluide par l’hélice, mesurée dans (R) :
4)a) à partir de ![]() .
.
4)b) en appliquant le principe de conservation de l’énergie à
un système convenable. On exprimera ![]() en fonction de
en fonction de ![]() et du débit massique
et du débit massique ![]() circulant dans le tube de courant représenté.
circulant dans le tube de courant représenté.
5) Application à la propulsion d’un vaisseau (avion,
navire) :
Le vaisseau a, par rapport à la terre où le fluide est immobile
à grande distance de l’hélice, une vitesse constante ![]() (
(![]() ). Le fluide
est éjecté vers l’arrière de l’hélice à une
vitesse
). Le fluide
est éjecté vers l’arrière de l’hélice à une
vitesse ![]() , à
grande distance de celle-ci,
, à
grande distance de celle-ci, ![]() étant mesurée par rapport à la terre.
étant mesurée par rapport à la terre.
5)a) Evaluer le rapport énergétique ![]() de la propulsion ;
de la propulsion ; ![]() est la puissance fournie à la coque du vaisseau, mesurée dans
le référentiel terrestre et
est la puissance fournie à la coque du vaisseau, mesurée dans
le référentiel terrestre et ![]() la puissance fournie par le moteur actionnant l’hélice.
la puissance fournie par le moteur actionnant l’hélice.
On exprimera h en fonction de u et ![]() .
Dans quelles conditions h est-il maximal ?
Que faut-il en penser ?
.
Dans quelles conditions h est-il maximal ?
Que faut-il en penser ?
5)b) A.N. : Calculer le rapport ![]() pour
pour ![]() (avion)
et
(avion)
et ![]() (navire)
(navire)
6) Application au fonctionnement d’une éolienne
Dans ce cas, (R) est le référentiel terrestre et ![]() .
.
6)a) Quelle est la forme du tube de courant ?
6)b) Soit P la puissance obtenue sur l’arbre de l’éolienne
. On pose ![]() ;
S et
;
S et ![]() étant
données, pour quelle valeur de x, la puissance P est-elle
maximale ?
étant
données, pour quelle valeur de x, la puissance P est-elle
maximale ?
6)c) Le rendement énergétique r est défini
comme le rapport de P au débit d’énergie cinétique
de l’air à travers la section ![]() du tube de courant. Exprimer r en fonction de x. Que vaut r
lorsque la puissance P est maximale ?
du tube de courant. Exprimer r en fonction de x. Que vaut r
lorsque la puissance P est maximale ?
6)d) A.N. : ![]() ;
;
![]() ; le diamètre
de l’hélice est 10 m ; calculer
; le diamètre
de l’hélice est 10 m ; calculer ![]() .
.
| Réponse 1 | Réponse 2 | Réponse 3 | Réponse 4a | Réponse 4b | Réponse 5a | Réponse 5b | Réponse 6a | Réponse 6b | Réponse 6c | Réponse 6d |
J) Ecoulement laminaire sur un plan incliné
|
Une couche mince de fluide incompressible (viscosité
On néglige les forces de viscosité sur
l'interface air/eau. |
|
Calculer les vitesses maximales pour ![]() et
et ![]() ,
,
| Réponse |
K) Ecoulement d’un fluide visqueux incompressible dans une conduite droite
Le fluide a pour masse volumique m, sa viscosité dynamique est appelée h. On néglige les effets du champ de pesanteur.
1) Ecoulement entre deux plans parallèles
|
Le fluide s’écoule suivant la direction x
entre les deux plans distants de 2h, de dimension infinie suivant
la direction z. Ainsi, l’écoulement est bidimensionnel suivant
les variables x, y. |
|
1)b) Montrer que l’équation de Navier-Stokes
conduit à : ![]() ;
;
![]() .
.
En déduire, compte tenu des conditions aux limites
en ![]() , que :
, que :
![]()
1)c) Calculer la vitesse moyenne de l’écoulement ![]() et la contrainte tangentielle à la paroi
et la contrainte tangentielle à la paroi ![]() .
.
1)d) Le nombre de Reynolds est défini par la relation ![]() où
où ![]() , appelé
diamètre hydraulique, est défini par la relation
, appelé
diamètre hydraulique, est défini par la relation ![]() (S : section de la conduite ; p : périmètre
de la section).
(S : section de la conduite ; p : périmètre
de la section).
Montrer que le coefficient de frottement défini par 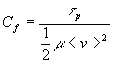 est égal à
est égal à ![]() .
.
Montrer que le coefficient de perte de charge défini
par 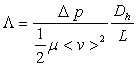 est égal
à
est égal
à ![]() (
(![]() représente la chute de pression pour une conduite de longueur
représente la chute de pression pour une conduite de longueur ![]() )
)
2) Reprendre la question 1) dans le cas d’une
conduite circulaire ; montrer que ![]() et
que
et
que ![]() ; écrire
la loi de Poiseuille c’est à dire la perte de charge par unité
de longueur en fonction du débit volumique.
; écrire
la loi de Poiseuille c’est à dire la perte de charge par unité
de longueur en fonction du débit volumique.
| Réponse 1a | Réponse 1b | Réponse 1c | Réponse 1d | Réponse 2 |
L) Viscosimètre de Couette
|
Cet appareil a été construit par COUETTE
pour mesurer la viscosité |
|
1) Montrer que le champ des vitesses du liquide peut
être écrit sous la forme : ![]()
2) Ecrire, au rayon r, la vitesse de glissement
entre deux couches de fluide successives. En déduire la force de viscosité
sur une surface de hauteur h , de rayon r, d'angle ![]() ainsi que le moment de cette force par rapport à l'axe de rotation.
ainsi que le moment de cette force par rapport à l'axe de rotation.
3) En écrivant que le moment des forces de viscosité
est égal au couple G exercé par le
moteur pour faire tourner le récipient, montrer que ![]() .
.
Calculer les coefficients A et B.
4) Calculer le couple moteur G connaissant l'angle de rotation a du cylindre intérieur mesuré à partir de sa position initiale correspondant à un récipient extérieur immobile.
5) Etudier le cas ![]() .
.
A.N. ![]() ;
; ![]() ;
; ![]() ; le récipient extérieur tourne à 90 tr/mn ; le
couple moteur est égal à
; le récipient extérieur tourne à 90 tr/mn ; le
couple moteur est égal à ![]()
| Réponse 1 | Réponse 2 | Réponse 3 | Réponse 4 | Réponse 5 |
M) Ecoulement d’un fluide autour d’un obstacle cylindrique ; effet Magnus
On considère un fluide incompressible (air à des faibles vitesses d’écoulement) de masse volumique m entourant un obstacle cylindrique de rayon R et d’axe Oz.
|
L’écoulement est à deux dimensions (vitesses
parallèles au plan xOy et indépendantes de z)
et stationnaire. Un point M du plan xOy est repéré
par ses coordonnées polaires L’écoulement est supposé irrotationnel. |
|
1) Dans cette partie, le fluide est parfait (viscosité
nulle).
1)1) Déduire que ![]() et que
et que ![]() .
.
1)2) Ecrire les conditions aux limites satisfait par le champ de vitesses
![]() au voisinage
de l’obstacle (
au voisinage
de l’obstacle (![]() ),
à l’infini (
),
à l’infini (![]() ).
).
1)3) Montrer qu’une solution type ![]() satisfait les équations du problème. On calculera les constantes
A et B, on exprimera les composantes du champ de vitesses
satisfait les équations du problème. On calculera les constantes
A et B, on exprimera les composantes du champ de vitesses ![]() .
Quelles remarques peut-on faire sur la forme générale du potentiel
.
Quelles remarques peut-on faire sur la forme générale du potentiel
![]() ?
?
On rappelle que ![]()
1)4) Calculer, à partir de l’équation
de Bernoulli, la pression ![]() [on
posera
[on
posera ![]() ] et déduire
la résultante des forces de pression qui s’exerce sur l’obstacle. Le
résultat est-il paradoxal ?
] et déduire
la résultante des forces de pression qui s’exerce sur l’obstacle. Le
résultat est-il paradoxal ?
2) Le fluide n’est plus parfait et on note h
sa viscosité dynamique.
On étudie une situation où le fluide est au repos à l’infini
et où le cylindre tourne autour de l’axe Oz à la vitesse
angulaire ![]() . A
cause des forces de viscosité, le fluide est mis en rotation, sa vitesse
. A
cause des forces de viscosité, le fluide est mis en rotation, sa vitesse
![]() est égale
à celle du cylindre pour
est égale
à celle du cylindre pour ![]() et diminue en s’éloignant.
et diminue en s’éloignant.
On suppose que l’écoulement est irrotationnel
2)1) Montrer que le champ des vitesses reste régi par des équations
de type ![]() et
et ![]() .
.
2)2) Chercher une solution à partir du potentiel ![]() .
.
2)3) Calculer, par un calcul direct, la circulation de ![]() sur une courbe fermée entourant le cylindre. N’y a t’il pas une contradiction
entre le résultat trouvé et la relation
sur une courbe fermée entourant le cylindre. N’y a t’il pas une contradiction
entre le résultat trouvé et la relation ![]() .
.
2)4) Montrer que, pour un fluide visqueux en écoulement
irrotationnel, l’équation de Navier-Stokes : 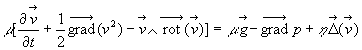 se ramène à celle d’Euler du fluide parfait.
se ramène à celle d’Euler du fluide parfait.
On pourra utiliser : ![]()
3) On superpose les situations 1) et 2) :
le cylindre tourne à vitesse angulaire ![]() dans un vent à vitesse
dans un vent à vitesse ![]() loin du cylindre. On suppose l’écoulement irrotationnel.
loin du cylindre. On suppose l’écoulement irrotationnel.
3)1) Montrer que le potentiel ![]() est solution de
est solution de ![]() et de
et de ![]() ;
calculer les composantes du champ de vitesses
;
calculer les composantes du champ de vitesses ![]() .
.
Comparer vitesse du fluide pour ![]() et vitesse du cylindre. En déduire que la solution trouvée pour
le champ des vitesses n’est pas totalement satisfaisante pour étudier
l’effet Magnus.
et vitesse du cylindre. En déduire que la solution trouvée pour
le champ des vitesses n’est pas totalement satisfaisante pour étudier
l’effet Magnus.
3)2) Calculer la pression ![]() [on
posera
[on
posera ![]() ] et déduire
la résultante des forces de pression appelée portance qui
s’exerce sur l’obstacle.
] et déduire
la résultante des forces de pression appelée portance qui
s’exerce sur l’obstacle.
Ecrire ce dernier résultat en introduisant la masse volumique du fluide,
le volume du cylindre, son vecteur rotation et la vitesse à l’infini
du fluide.
Le résultat vous paraît-il en accord avec vos observations courantes
sur le mouvement des balles ou ballons ?
4) En transposant les résultats précédents et en introduisant le forces de pesanteur et les forces de frottement supposées proportionnelles au vecteur vitesse, écrire l’équation fondamentale de la dynamique pour le mouvement du centre de masse d’un mobile de type balle de golf, tennis, tennis de table ou ballon de football, de rugby.
| Réponse 11 | Réponse 12 | Réponse 13 | Réponse 14 | Réponse 21 | Réponse 22 | Réponse 23 | Réponse 24 | Réponse 31 | Réponse 32 | Réponse 4 |
N) Equation de propagation de l’onde sonore ; vitesse du son
L’onde sonore (ou acoustique) est assimilée à
la propagation d’une perturbation de pression ![]() .
Dans le cadre de l’approximation acoustique, on considère que :
.
Dans le cadre de l’approximation acoustique, on considère que :
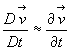 ,
,
1) Montrer que la propagation de l’onde sonore est régi par les équations :
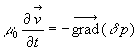 en négligeant les effets de la pesanteur
en négligeant les effets de la pesanteur
2) En déduire l’équation de propagation
vérifiée par ![]() et la vitesse de phase c (vitesse du son).
et la vitesse de phase c (vitesse du son).
Montrer que, pour un gaz parfait,  .
.
Application numérique pour l’air dans des conditions normales
de pression et température.
O) Tuyère supersonique
|
L’écoulement d’un gaz supposé parfait s’effectue
d’une région R1 à une région
R2 à travers une conduite (tuyère) de
section variable. L’écoulement est permanent, adia-batique, en
première approximation mono-dimensionnel et on néglige les
effets de la pesanteur. |
|
Loin en amont du col, la pression est ![]() ,
la masse volumique
,
la masse volumique ![]() ,
la température
,
la température ![]() et la vitesse
et la vitesse ![]() pratiquement nulle.
pratiquement nulle.
1) En écrivant, d’une part la conservation de
la masse, et d’autre part l’équation de Bernoulli entre deux points infiniment
voisins de l’écoulement, démontrer la formule d’Hugoniot :
![]() si, à
l’endroit considéré, S est la section de la conduite, v
la vitesse de l’écoulement, c la vitesse du son et
si, à
l’endroit considéré, S est la section de la conduite, v
la vitesse de l’écoulement, c la vitesse du son et ![]() le nombre de Mach.
le nombre de Mach.
En déduire que :
2) Une tuyère supersonique est calculée
de telle sorte qu’au col la vitesse de l’écoulement soit égale
à celle du son si bien qu’en amont la vitesse de l’écoulement
est inférieure à celle du son alors qu’en aval elle est supérieure.
On notera enfin que vitesse de l’écoulement et vitesse du son à
un endroit dépendent des caractéristiques du fluide à cet
endroit c’est à dire de sa pression p, de sa masse volumique m
et de sa température T.
2)a) A partir de l’équation de St Venant, établir la relation
![]() où
où ![]() sont respectivement les vitesses du son au col et loin en amont du col (on négligera
sont respectivement les vitesses du son au col et loin en amont du col (on négligera
![]() et on notera
et on notera
![]() la pression,
la masse volumique et la température au col).
la pression,
la masse volumique et la température au col).
2)b) En déduire que ![]() ;
;
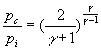 ;
; 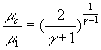
2)c) Montrer :
que 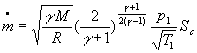 et que
et que 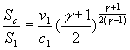
| Réponse 1 | Réponse 2a | Réponse 2b | Réponse 2c |
P) Etude (simplifiée) des mouvements d'air de l'atmosphère dans un plan horizontal
|
La Terre est assimilée à une sphère
de rayon |
|
Pour les mouvements dans un plan horizontal, le vent, même
dans les conditions d'une tornade, peut être considéré comme
un écoulement hydrodynamique pour lequel nous négligerons les
forces de viscosité.
On limite l'étude à des mouvements d'air définis par ![]()
1) Montrer que la composante ![]() ne dépend pas de q .
ne dépend pas de q .
2) Ecrire
les composantes de l'équation d'Euler sur les axes (![]() )
et en déduire que les isobares sont des cercles de rayon r.
)
et en déduire que les isobares sont des cercles de rayon r.
3) Une zone de hautes pression (anticyclone) est caractérisée par une surpression maximale en O de 10 hectopascals et un rayon de 1000 km.
3)a) Simplifier l'équation d'Euler et calculer
un ordre de grandeur de v(r) pour ![]()
3)b) Doit-on faire une différence entre l'hémisphère Nord et l'hémisphère Sud ?
3)c) Les photos météorologiques montrent des mouvements d'air en forme de spirale. Expliquer en quoi l'étude précédente est très simplifiée.
4) Tornade
Une tornade est un mouvement d'air violent sur une faible étendue que l'on modélise :
On prendra ![]() et une vitesse maximale du vent égale à 60 m/s.
et une vitesse maximale du vent égale à 60 m/s.
4)a) Calculer la vitesse en tout point. En déduire la valeur numérique de w. Quelle est la vitesse dans "l'œil du cyclone".
4)b) Simplifier l'équation d'Euler.
4)c) En déduire et représenter la fonction
p(r). Exprimer ![]() .
Application numérique.
.
Application numérique.
| Réponse
1 | Réponse
2 | Réponse
3a | Réponse
3b | Réponse
3c | Réponse
4a | Réponse
4b | Réponse
4c |
Q) Etude de la houle
|
L'eau est considérée comme un fluide de
masse volumique m . Au repos, la surface
libre de séparation air-eau est prise comme origine de l'axe vertical. |
|
Dans un modèle bidimensionnel, la vitesse d'une "particule"
fluide, de position (x, z) -position au repos ![]() -
est de la forme :
-
est de la forme :
![]() en notation
complexe.
en notation
complexe.
La pression est de la forme ![]() .
.
Lorsque le fluide est au repos, la pression est donnée
par ![]()
1) Ecrire les équations qui permettent de calculer
![]()
2) Résoudre
ces équations pour le cas particulier ![]() (houle en eau profonde) dans l'approximation
(houle en eau profonde) dans l'approximation 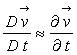 que l'on justifiera à partir des données numériques.
que l'on justifiera à partir des données numériques.
En déduire la célérité des ondes ainsi que la trajectoire
d'une particule fluide à une altitude ![]() .
.
R) Oscillations d’un liquide dans un tube coudé
1) La pression ![]() et la vitesse
et la vitesse ![]() à l’instant
à l’instant ![]() ,
en un point
,
en un point ![]() d’une ligne de courant repéré par son abscisse curviligne
d’une ligne de courant repéré par son abscisse curviligne ![]() (
(![]() origine sur
la ligne de courant de l’abscisse curviligne) sont liées par l’équation
d’Euler.
origine sur
la ligne de courant de l’abscisse curviligne) sont liées par l’équation
d’Euler.
Le champ de pesanteur est donné par ![]() ,
où
,
où ![]() est le
vecteur unitaire de l’axe vertical
est le
vecteur unitaire de l’axe vertical ![]() ascendant et on désigne par
ascendant et on désigne par ![]() la côte de
la côte de ![]() .
.
1)a) Montrer que l’équation d’Euler peut être
écrite :
![]()
1)b) Montrer que, pour un fluide incompressible dont l’écoulement
est tel que ![]() soit indépendant
de
soit indépendant
de ![]() , la relation du 1)a)
s’intègre sous la forme :
, la relation du 1)a)
s’intègre sous la forme :
![]()
1)c) Montrer que l’équation 1)b) est bien adapté
au mouvement d’un fluide incompressible dans un tube de faible section ![]() .
.
2)
|
On envisage les deux tubes ci-contre de section |
|
|
L’origine de l’axe vertical ![]() ainsi que de l’origine de l’abscisse curviligne correspond est prise à
la position d’équilibre.
ainsi que de l’origine de l’abscisse curviligne correspond est prise à
la position d’équilibre.
Calculer la période des oscillations.
| Réponse 1a | Réponse 1b | Réponse 1c | Réponse 2 |
S) Turbine
|
Une conduite cylindrique amène l’eau d’un barrage
(dont le niveau est maintenu constant) dans une turbine. |
|
T) Pompe
Une pompe à essence de rendement ![]() assure, en un temps
assure, en un temps ![]() ,
le remplissage d’un réservoir d’automobile d’une contenance
,
le remplissage d’un réservoir d’automobile d’une contenance ![]() .
Elle aspire l’essence (
.
Elle aspire l’essence (![]() )
dans une grande citerne dont la surface libre est à la pression atmosphérique
)
dans une grande citerne dont la surface libre est à la pression atmosphérique
![]() .
.
Elle refoule l’essence sous forme d’un jet cylindrique, en contact avec l’atmosphère,
se déversant dans le réservoir. La différence des cotes
entre la section de sortie de la conduite et la surface libre de la citerne
est ![]() . La conduite
a une longueur
. La conduite
a une longueur ![]() et un diamètre
et un diamètre ![]() .
.
La viscosité de l’essence est ![]()
Calculer la puissance ![]() de la pompe.
de la pompe.
N.B. Le coefficient de perte de charge sera pris égal
à ![]() si
l’écoulement est laminaire, à
si
l’écoulement est laminaire, à ![]() si l’écoulement est turbulent.
si l’écoulement est turbulent.
| Réponse 1 |