et une permittivité électrique 
dépendant de l’espace.On se propose d’étudier, dans ce diélectrique, la propagation d’ondes électromagnétiques notées :
; 
Equations de Maxwell et Théorème de Malus
Problème
Un diélectrique linéaire, isotrope, inhomogène
est caractérisé en chaque point par la perméabilité
magnétique
et une permittivité électrique
dépendant de l’espace.
On se propose d’étudier, dans ce diélectrique, la propagation
d’ondes électromagnétiques notées :
;
où 
est une fonction de l’espace (
)
et 
le module du
vecteur d’onde d’une radiation de pulsation 
se propageant dans le vide : 
1) A partir des expressions de 
et 
, montrer que :
.
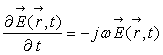
2) Ecrire les équations de Maxwell
3) L’Optique géométrique est une solution
approchée des équations de Maxwell pour les faibles longueurs
d’ondes (
)
3)a) Réécrire les équations de la question 2)
pour 
.
3)b) Préciser alors la structure locale du champ électromagnétique.
Quelle est la direction du vecteur de Poynting ? A quoi correspondent les
surfaces 
?
3)c) Soient 
le vecteur unitaire de la direction portant le vecteur de Poynting et 
l’indice du milieu au point M.
Montrer que la fonction 
est solution de l’équation 
Remarque : cette équation est l’expression différentielle du théorème de Malus qui peut être pris comme point de départ de l’Optique géométrique.
| Réponse 1 | Réponse 2 | Réponse 3a | Réponse 3b | Réponse 3c |