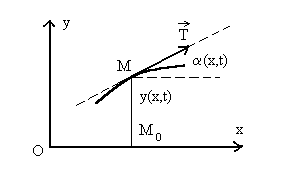
Corde vibrante. L'équation de d'Alembert et ses solutions
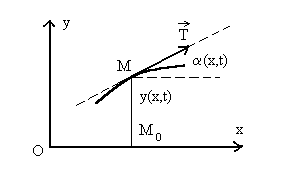
Une corde sans raideur, inextensible, de masse linéique
constante ![]() ,
est tendue par une tension
,
est tendue par une tension ![]() .
Au repos, elle se confond avec l'axe
.
Au repos, elle se confond avec l'axe ![]() .
.
De part et d'autre de cette position d'équilibre, on étudie les
petits mouvements transversaux de cette corde dans le plan ![]() ,
en admettant qu'un élément de corde au repos (point
,
en admettant qu'un élément de corde au repos (point ![]() )
reste pendant le mouvement à la même abscisse. L'élongation
d'un point d'abscisse
)
reste pendant le mouvement à la même abscisse. L'élongation
d'un point d'abscisse ![]() à l'instant
à l'instant ![]() (point
(point ![]() ) est notée
) est notée
![]() . La tangente
en
. La tangente
en ![]() à
la corde fait avec l'axe
à
la corde fait avec l'axe ![]() un angle
un angle ![]() qui
reste petit, ce qui suppose que
qui
reste petit, ce qui suppose que ![]()
Enfin,
l'action du champ de pesanteur sur le mouvement, ainsi que toute cause d'amortissement
sont négligées.
1. Équation d'onde pour un ébranlement le long de la corde
1)a) La longueur de la corde varie très peu lorsqu'elle
vibre. Montrer qu'à des termes du second ordre en ![]() près, l'abscisse curviligne
près, l'abscisse curviligne ![]() peut être confondue avec l'abscisse
peut être confondue avec l'abscisse ![]() .
.
1)b) On admet que la tension ![]() reste, en tout point, tangente à la corde.
reste, en tout point, tangente à la corde.
Écrire la relation fondamentale de la dynamique pour un élément
de corde compris entre ![]() et
et ![]() .
.
Montrer à l'aide des hypothèses faites que la tension ![]() est de module constant, noté
est de module constant, noté ![]() ,
et que l'ébranlement est régi par l'équation :
,
et que l'ébranlement est régi par l'équation :
![]()
Exprimer la constante ![]() en fonction de
en fonction de ![]() et
et ![]() et donner
ses dimensions.
et donner
ses dimensions.
| Réponse 1a | Réponse 1b |
2. Solution en ondes progressives de l'équation de d'Alembert
2)a) Introduire les grandeurs ![]() et
et ![]() et donner
l'équation différentielle de la fonction
et donner
l'équation différentielle de la fonction ![]() .
.
En
déduire que la solution peut s'écrire sous la forme ![]() .
.
2)b) Interpréter la solution précédente
et donner la signification du paramètre ![]() .
.
AN1 : Calculer ![]() pour une cordelette (type de Melde) en coton ou nylon de 1 gramme par mètre
tendue sur une poulie par une masse de
pour une cordelette (type de Melde) en coton ou nylon de 1 gramme par mètre
tendue sur une poulie par une masse de ![]() .
.
AN2
: Calculer v pour une corde d'acier de masse volumique ![]() ,
de rayon
,
de rayon ![]() ,
tendue par une
,
tendue par une
| Réponse 2a | Réponse 2b |
3. Solution en ondes stationnaires de l'équation de d'Alembert
A présent la corde de longueur ![]() est fixée en ses extrémités, deux points de l'axe
est fixée en ses extrémités, deux points de l'axe ![]() d'abscisse
d'abscisse ![]() .
.
3)a) On cherche des solutions de l'équation
(1) sous la forme de variables séparées : ![]()
Montrer
que ![]() doivent être
des fonctions sinusoïdales. En notant
doivent être
des fonctions sinusoïdales. En notant ![]() la pulsation de
la pulsation de ![]() ,
quelle est la pulsation
,
quelle est la pulsation ![]() ?
?
3)b) Montrer que les conditions aux limites imposent
à ![]() de
ne pouvoir prendre qu'une série de valeurs discrètes notées
de
ne pouvoir prendre qu'une série de valeurs discrètes notées
![]() et en
donner l'expression. En déduire que pour des grandeurs
et en
donner l'expression. En déduire que pour des grandeurs ![]() fixées, la longueur d'onde
fixées, la longueur d'onde ![]() ne
peut elle-même prendre qu'une suite de valeurs
ne
peut elle-même prendre qu'une suite de valeurs ![]() .
Exprimer la longueur
.
Exprimer la longueur ![]() en fonction de
en fonction de ![]() .
.
3)c) Quelle est l'expression d'une solution ![]() correspondant au mode de vibration d'indice
correspondant au mode de vibration d'indice ![]() ?
En déduire qu'une solution générale de l'équation
(1) s'écrit sous la forme (2) d'une série de Fourier :
?
En déduire qu'une solution générale de l'équation
(1) s'écrit sous la forme (2) d'une série de Fourier : ![]() (2)
(2)
3)d) Montrer que l'équation (2) peut être
écrite sous la forme ![]()
3)e) Justifier le terme d'onde stationnaire donné
à ![]() (mode
(mode
![]() ). Montrer qu'il
existe le long de la corde, outre les extrémités, des points immobiles
; en préciser le nombre et la position.
). Montrer qu'il
existe le long de la corde, outre les extrémités, des points immobiles
; en préciser le nombre et la position.
En supposant qu'à l'instant ![]() ,
la corde coïncide avec l'axe
,
la corde coïncide avec l'axe ![]() ,
représenter graphiquement l'état des déformations de la
corde aux instants
,
représenter graphiquement l'état des déformations de la
corde aux instants ![]() avec
avec ![]() dans les
cas
dans les
cas ![]() .
.
AN : Pour une corde de longueur ![]() ,
oscillant à la fréquence
,
oscillant à la fréquence ![]() ,
donner la tension
,
donner la tension ![]() à appliquer pour obtenir le seul mode
à appliquer pour obtenir le seul mode ![]() .
En déduire
.
En déduire ![]() pour
pour ![]() (fréquence
propre la plus basse),
(fréquence
propre la plus basse), ![]() ,
,
![]() ,
, ![]() .
Quelle note musicale reconnaissez-vous ?
.
Quelle note musicale reconnaissez-vous ?
| Réponse 3a | Réponse 3b | Réponse 3c | Réponse 3d | Réponse 3e |
4.1. Corde de piano
A l'instant ![]() ,
la corde est immobile dans la position d'équilibre
,
la corde est immobile dans la position d'équilibre ![]() .
Elle est frappée avec un petit marteau de largeur
.
Elle est frappée avec un petit marteau de largeur ![]() (avec
(avec ![]() ) situé
entre les abscisses
) situé
entre les abscisses ![]() ,
qui communique par le choc une impulsion initiale à la partie frappée.
Dans ces conditions, la vitesse de chaque point de la corde à l'instant
,
qui communique par le choc une impulsion initiale à la partie frappée.
Dans ces conditions, la vitesse de chaque point de la corde à l'instant
![]() est modélisée
par une fonction " créneau " :
est modélisée
par une fonction " créneau " :
![]() pour
pour ![]() et
et ![]() partout ailleurs.
partout ailleurs.
4)1)a) Déterminer les coefficients ![]()
4)1)b) Trouver une application musicale du fait que les coefficients
dépendent de a. Que faut-il faire pour supprimer un harmonique,
en particulier celui correspondant à ![]() ?
?
4)1)c) Dans le cas ![]() ,
quels sont les harmoniques présents ?
,
quels sont les harmoniques présents ?
4.2. Corde de clavecin, de guitare ou de harpe
La même corde est pincée et lâchée
au temps ![]() de telle
sorte que sa vitesse initiale soit nulle. L' endroit
de telle
sorte que sa vitesse initiale soit nulle. L' endroit ![]() où a lieu le pincement joue le même rôle vis à vis
des harmoniques que celui de la frappe. En conséquence, et afin de limiter
les calculs, nous nous limitons à un pincement en
où a lieu le pincement joue le même rôle vis à vis
des harmoniques que celui de la frappe. En conséquence, et afin de limiter
les calculs, nous nous limitons à un pincement en ![]() si bien que la position initiale de la corde est définie par la "
fonction triangle " :
si bien que la position initiale de la corde est définie par la "
fonction triangle " : 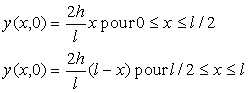
4)2)a) Déterminer les coefficients ![]()
4)2)b) Comparer les spectres d'uns corde à piano et d'une corde
à clavecin et apprécier la différence de timbre sonore.
4)2)c) Pour une corde de guitare ou de harpe, le pincement peut être
effectuée " délicatement " avec un doigt de telle sorte
que la position initiale soit définie par la " fonction parabole
": ![]() . Reprendre
les calculs dans ce cas et conclure.
. Reprendre
les calculs dans ce cas et conclure.
| Réponse 41a | Réponse 41b | Réponse 41c | Réponse 42a | Réponse 42b | Réponse 42c |
5. Oscillations entretenues
Expliquer ce qui se passe si, l'extrémité ![]() étant fixée, on place en
étant fixée, on place en ![]() un vibreur de très faible amplitude de telle sorte que
un vibreur de très faible amplitude de telle sorte que ![]() .
.
| Réponse 5 |
6. Réflexion et transmission sur discontinuité
|
|
Une corde très longue est composée de deux
tronçons de masses linéiques Du coté
|
Montrer qu'en plus de l'onde incidente, il existe une onde
réfléchie ![]() du coté
du coté ![]() et une onde transmise
et une onde transmise ![]() du coté
du coté ![]() .
Donner leur expression générale. Exprimer deux relations différentielles
satisfaites par ces ondes au point
.
Donner leur expression générale. Exprimer deux relations différentielles
satisfaites par ces ondes au point ![]() et en déduire l'expression des coefficients de réflexion et de
transmission
et en déduire l'expression des coefficients de réflexion et de
transmission ![]() ; entre quelles limites peuvent-ils varier ? Discuter ces cas suivant la valeur
du coefficient
; entre quelles limites peuvent-ils varier ? Discuter ces cas suivant la valeur
du coefficient ![]() .
.
| Réponse 6 |