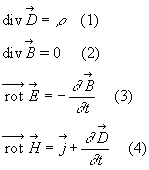Les équations de Maxwell
Plan
1. Introduction
1.1. Rappel des lois de base en électricité
1.2. La conservation de la charge
1.3. Equation de Maxwell - Ampère
2. Les équations de Maxwell
3. Cas des conducteurs
1. Introduction
1.1. Rappel des lois de base en électricité
- L'étude de l'électrostatique nous a permis d'établir
la relation
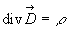 où l'induction électrique est égale à
où l'induction électrique est égale à 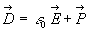 .
.
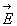 est le champ électrique
et
est le champ électrique
et  le vecteur
polarisation.
le vecteur
polarisation.
Ces relations sont vraies dans un diélectrique et dans un conducteur.
Pour un conducteur en équilibre électrostatique ou en électrocinétique
des courants continus, la polarisation 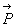 est nulle et la densité volumique de charges
est nulle et la densité volumique de charges 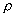 est nulle. Nous avons vu que la loi d’Ohm pouvait être étendue
à des régimes variables et ceci amène à envisager,
pour les conducteurs, l’extension de ces relations à des régimes
variables.
est nulle. Nous avons vu que la loi d’Ohm pouvait être étendue
à des régimes variables et ceci amène à envisager,
pour les conducteurs, l’extension de ces relations à des régimes
variables.
En ce qui concerne les diélectriques, il convient de s’interroger
sur ce que devient la polarisation en présence d’un champ électrique
variable. Pour des champs lentement variables (basses fréquences),
l’inertie mécanique de la matière ne sera pas sensible et
la polarisation sera identique. A hautes fréquences, la polarisation
de molécules non polaires ou la polarisation par orientation aura
du mal à se réaliser à cause de cette inertie et la
capacité de polarisation du milieu sera diminué. Le vecteur
polarisation dépendra du temps (la permittivité électrique
dépendra de la fréquence) ce qui ne change pas (mis à
part les temps de propagation) le raisonnement fait pour introduire le
vecteur induction.
Ainsi, sauf infirmation expérimentale, on peut envisager
ces relations pour des régimes variables.
- L'étude de la magnétostatique nous a permis d'établir
les relations
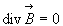 et
et 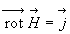 où
l'excitation (appelé aussi champ) magnétique est égale
à
où
l'excitation (appelé aussi champ) magnétique est égale
à 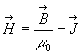
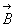 est le champ (ou
induction) magnétique,
est le champ (ou
induction) magnétique, 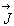 le vecteur aimantation et
le vecteur aimantation et 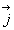 le vecteur densité de courant.
le vecteur densité de courant.
Là encore, sauf infirmation expérimentale, on peut
envisager ces relations pour des régimes variables.
- L'étude du phénomène d'induction nous a conduit à
la relation
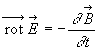
Ces relations permettent d'introduire un potentiel vecteur 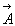 et un potentiel scalaire V.
et un potentiel scalaire V.
En effet 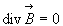 ð
ð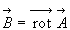
Le report de cette dernière relation dans 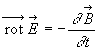 ð
ð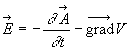
Rappelons que le potentiel vecteur et le potentiel scalaire ne sont
pas définis de manière unique, à un gradient additif
près pour le premier et à une constante additive près
pour le second.
1.2. La conservation de la charge
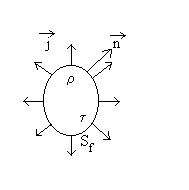 |
Un volume 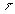 ,
délimité par une surface ,
délimité par une surface 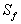 ,
contient une charge ,
contient une charge 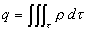 . .
Le vecteur unitaire normal est orienté vers l'extérieur
au volume.
On rappelle qu'à chaque particule est attaché une charge
multiple entier de la charge élémentaire.
Le flux d'électricité qui sort du volume s'écrit 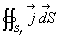 |
La conservation de la charge (des particules) s'écrit : 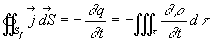
L'application du théorème d'Ostrogradsky conduit à l'expression
locale de conservation de la charge 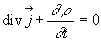
1.3. Equation de Maxwell-Ampère
Il y a incompatibilité entre l'équation de conservation de la
charge et le théorème d'Ampère 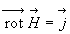 qui conduit à
qui conduit à 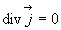 .
.
Renoncer à la conservation de la charge c'est renoncer à
la conservation des particules ou renoncer à la notion de charge
élémentaire indépendante de tout référentiel.
Maxwell a proposé de modifier le théorème d'Ampère
sous la forme 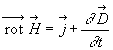 .
.
Cette expression est compatible avec la conservation de la charge, le terme 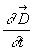 est appelé courant de déplacement.
est appelé courant de déplacement.
Si nous voulons nous persuader de sa nécessité sur un
exemple simple. Considérons, en régime variable, un circuit
électrique avec un condensateur. Dans les fils conducteurs, le courant
est du à un mouvement de charges. Entre les armatures, le mouvement
de charges n'est plus possible, sans le courant de déplacement il
n'y aurait pas possibilité de circuit électrique comprenant
des condensateurs.
2. Les équations de Maxwell
Les équations de Maxwell régissent les
phénomènes électriques
Remarques :
- comme toute théorie en Physique, ces équations ne sont
validées que par les expériences,
- les équations 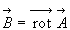 et
et 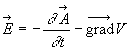 restent
valables,
restent
valables,
- la relation de jauge de Coulomb n’est valable que pour les régimes
permanents ; pour les régimes variables, elle sera modifié
en relation de jauge de Lorentz (voir théorie des ondes électromagnétiques).
Conditions de passage à la surface de séparation de
deux milieux
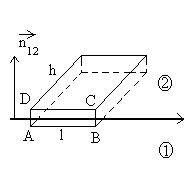 |
Les points A et B sont dans le milieu 1, les
points C et D dans le milieu 2. Dans les raisonnements, on fera tendre
A et D d'une part, B et C d'autre part l'un vers l'autre.
-
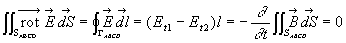 puisque
la surface puisque
la surface 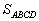 tend vers 0.
tend vers 0.
soit 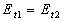
|
-
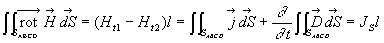
soit 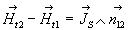 où
où 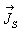 est
le courant surfacique.
est
le courant surfacique.
- Nous envisageons le parallélogramme de base ABCD de profondeur h
; Nous appelons
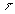 qui tend vers 0 si A et D, B et C tendent l'un vers l'autre.
qui tend vers 0 si A et D, B et C tendent l'un vers l'autre.
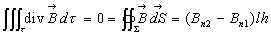 soit
soit 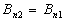
-
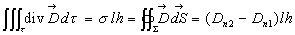
soit 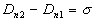 où
où 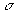 est
la densité superficielle de charge.
est
la densité superficielle de charge.
A ces équations, il convient d'ajouter la continuité
du potentiel.
3. Cas des conducteurs
-
Nous nous situons dans des domaines de fréquence où la loi
d'Ohm est applicable.
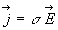 (
(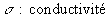 ),
), 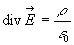 et
et 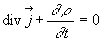 ð
ð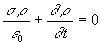 ð
ð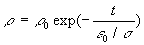 en
supposant qu'au temps
en
supposant qu'au temps 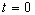 ,
lors de l'application du champ électrique
,
lors de l'application du champ électrique 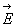 ,
la densité volumique de charge puisse devenir différente de 0.
,
la densité volumique de charge puisse devenir différente de 0.
Pour le cuivre, 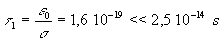 temps d'établissement du régime.
temps d'établissement du régime.
Ainsi la densité volumique de charge redevient nulle dans des
temps beaucoup plus courts que les temps d'établissement des régimes
dans le cadre de la loi d'Ohm.
- On appelle conducteur parfait le cas limite où la conductivité
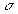 est infinie.
est infinie.
Le champ électrique ne peut être que nul sinon la puissance
dissipée par effet Joule serait infinie.
Ceci veut dire qu'on ne peut imposer un champ électrique à
l'intérieur d'un matériau de conductivité infinie.
Instantanément, il retrouve un équilibre électrostatique.
En conséquence le champ magnétique sera lui aussi nul.
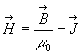
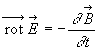
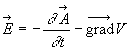

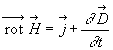 .
.