Exercices sur le phénomène d'induction
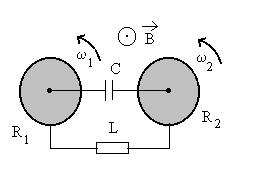
1) On réalise le montage suivant :
|
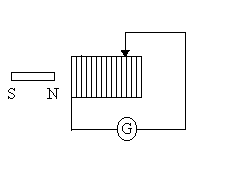
|
Un aimant est placé devant un rhéostat
à curseur en série avec un galvanomètre G. L’axe
pôle Sud-pôle Nord de l’aimant et l’axe du rhéostat
sont confondus.
1)a) On déplace l’aimant suivant son axe.
Qu’observe t’on ? Quels sont les changements si on change le sens
du déplacement ou si on inverse le pôle Sud et le pôle
Nord ? A quelle cause attribuée le phénomène
observée ?
|
1)b) On déplace le rhéostat. Mêmes
questions qu’en 1)a)
1)c) En considérant que le mouvement de l’aimant (ou du rhéostat)
suppose que le référentiel du rhéostat (ou de l’aimant)
est fixe, est ce que les causes envisagées en 1)a) et 1)b)
sont différentes ?
1)d) L’aimant et le rhéostat étant fixes, on déplace
le curseur (le nombre de spires du circuit électrique change. Qu'observe
t’on ?
| Réponse
1a | Réponse
1b | Réponse
1c | Réponse
1d |
2) Un avion métallique d’envergure 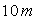 vole horizontalement à la vitesse de
vole horizontalement à la vitesse de 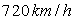 dans le champ magnétique terrestre dont la composante verticale a pour
module
dans le champ magnétique terrestre dont la composante verticale a pour
module 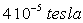 .
.
2)a) Quelle est la différence de potentiel entre les extrémités
des ailes ? Comment peut-on la mesurer ?
2)b) Mêmes questions si l’avion est en bois.
| Réponse
2a | Réponse
2b |
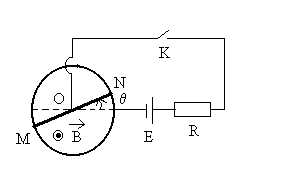
3) Une tige MN (longueur 2a, résistance
2r, masse m) est mobile autour de l’axe vertical  .
Ses extrémités
.
Ses extrémités  glissent sur une spire circulaire de résistance négligeable. L’ensemble
est placé dans un champ magnétique
glissent sur une spire circulaire de résistance négligeable. L’ensemble
est placé dans un champ magnétique  uniforme perpendiculaire au plan de la spire.
uniforme perpendiculaire au plan de la spire.
|
|
A 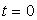 ,
la barre est immobile à la position ,
la barre est immobile à la position 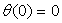 et on ferme l’interrupteur.
et on ferme l’interrupteur.
On se propose de déterminer 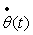 et et
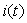 , courant
électrique dans la branche du générateur, sachant
que la tige est soumise à un couple de frottement , courant
électrique dans la branche du générateur, sachant
que la tige est soumise à un couple de frottement 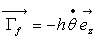
3)1) Etablir l’équation électrique
et l’équation différentielle du mouvement.
|
3)2) Avant de procéder à l’intégration
de l’équation du mouvement et de l’équation électrique,
on établira un bilan énergétique.
| Réponse
31 | Réponse
32 |
4) Deux barres conductrices (résistance totale
r, longueur de chaque barre a, masse de chaque barre m)
glissent sur deux rails conducteurs parallèles (résistances négligeables,
distants de 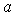 ),
situés dans le même plan horizontal.
),
situés dans le même plan horizontal.
Les milieux des barres sont reliés entre eux par un ressort de raideur
k et de longueur à vide 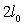 ,
le mouvement des barres est perpendiculaire aux rails.
,
le mouvement des barres est perpendiculaire aux rails.
L’ensemble est plongé dans un champ magnétique uniforme  perpendiculaire au plan des rails. On néglige les phénomènes
d’auto-inductance.
perpendiculaire au plan des rails. On néglige les phénomènes
d’auto-inductance.
A l’instant 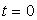 ,
les vitesses sont nulles et le ressort a une longueur
,
les vitesses sont nulles et le ressort a une longueur 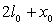 .
.
On veut déterminer les positions 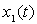 et
et 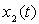 de chaque
barre repérée par rapport à leur position respective lorsque
le ressort n'est pas allongé.
de chaque
barre repérée par rapport à leur position respective lorsque
le ressort n'est pas allongé.
4)1) Etablir l’équation électrique et
les deux équations différentielles du mouvement.
4)2) Avant de procéder à l’intégration
des équations du mouvement et de l’équation électrique,
établir un bilan énergétique.
5) Deux roues de Barlow 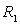 et
et 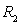 identiques (masse
identiques (masse
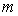 , rayon
, rayon 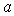 )
sont plongées dans un champ magnétique uniforme
)
sont plongées dans un champ magnétique uniforme  perpendiculaire au plan contenant les roues. Elles sont branchées en
série avec un condensateur de capacité
perpendiculaire au plan contenant les roues. Elles sont branchées en
série avec un condensateur de capacité 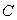 et une inductance
et une inductance 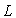 .
.
5)2) Avant de procéder à l’intégration des équations
du mouvement et de l’équation électrique, établir un bilan
énergétique.
5)3) Le lecteur pourra reprendre cet exercice en changeant
les conditions initiales et/ou le circuit électrique (résistance
non négligeable, générateur de tension, éléments
constitutifs).
| Réponse
51 | Réponse
52 |
6) On considère N solénoïdes
identiques (n spires par unité de longueur ; longueur l ;
rayon a) disposés en étoile (les axes de deux solénoïdes
consécutifs font un angle 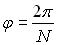 ).
).
|
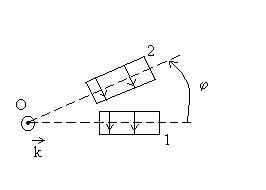
|
Ils sont parcourus par les courants respectifs 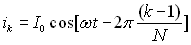 avec k appartenant à l’intervalle
avec k appartenant à l’intervalle 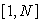 . .
6)1) Déterminer le champ magnétique
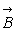 en O. en O.
|
6)2) Un dipôle magnétique 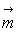 (perpendiculaire à
(perpendiculaire à 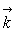 )
a un mouvement de rotation d’axe
)
a un mouvement de rotation d’axe 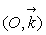 à la vitesse angulaire constante
à la vitesse angulaire constante 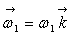 .
.
Déterminer le couple moyen s’exerçant sur le dipôle.
| Réponse
61 | Réponse
62 |
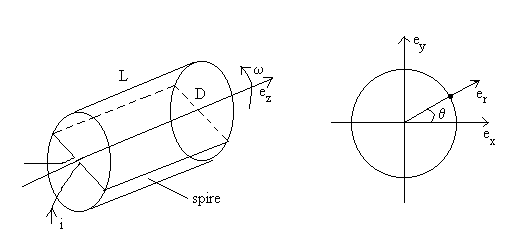
7) Etude électromagnétique d’un moteur
Dans un laboratoire lié à un référentiel
galiléen, un cylindre solide, isolant, est en rotation à la vitesse
angulaire 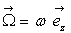 .
.
Sur ce cylindre, qui constitue le rotor d’un moteur, sont enroulées,
de manière régulière et continue, N spires rectangulaires
(voir figure) parcourues par un courant i. La position d’une spire est
repérée par l’angle 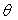 que fait son plan avec la direction
que fait son plan avec la direction 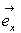 .
.
Soient 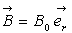 le
champ magnétique à la périphérie du rotor.
le
champ magnétique à la périphérie du rotor.
7)1) Montrer que, d’un point de vue électrique,
ce système se comporte comme un récepteur de force contre-électromotrice
 de résistance
de résistance
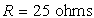 , parcouru par
le courant i (on néglige l’inductance propre du bobinage).
, parcouru par
le courant i (on néglige l’inductance propre du bobinage).
7)2) Montrer que, d’un point de vue mécanique,
le rotor de moment d’inertie J par rapport à l’axe de rotation
est soumis à un couple de forces électromagnétiques 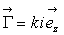
7)3) L’induit est alimenté par un amplificateur
de tension, commandé par une tension u. Son coefficient d’amplification
est 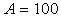 et sa résistance
de sortie
et sa résistance
de sortie 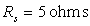 .
.
7)3)a) Faire un schéma électrique équivalent à
l’ensemble moteur-amplificateur
7)3)b) Montrer que 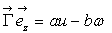
7)3)c) Ecrire l’équation différentielle en tenant compte
des frottements par un couple 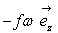
7)3)d) Le moteur est initialement alimenté sous une tension 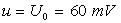 et tournant en régime permanent à la vitesse
et tournant en régime permanent à la vitesse 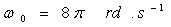 ,
on le soumet brutalement à
,
on le soumet brutalement à 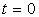 à
un échelon
à
un échelon 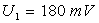
Calculer 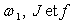 si la
constante de temps du régime transitoire est 125 ms et si
si la
constante de temps du régime transitoire est 125 ms et si 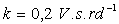
| Réponse
71 | Réponse
72 | Réponse
73a | Réponse
73b | Réponse
73c | Réponse
73d |
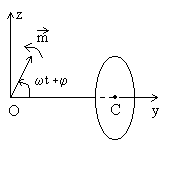
8) Un moment magnétique 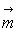 contenu
dans un plan Oyz tourne autour de l’axe Ox à la vitesse
angulaire constante
contenu
dans un plan Oyz tourne autour de l’axe Ox à la vitesse
angulaire constante 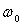 .
.
|
|
Une spire S d’axe Oy, de résistance
R et de coefficient d’auto-induction L, est placée
à une distance D de O. Son rayon est a.
Déterminer le couple moyen 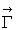 que doit exercer l’opérateur pour maintenir constante la vitesse
angulaire
que doit exercer l’opérateur pour maintenir constante la vitesse
angulaire 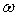 de rotation du dipôle magnétique (on se placera en régime
établi ; la spire est fixe)
de rotation du dipôle magnétique (on se placera en régime
établi ; la spire est fixe)
|
| Réponse
8 |
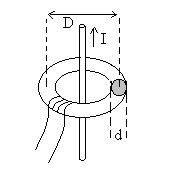
9) Pince ampermétrique
9)b) Calculer la f.e.m. induite aux bornes des spires. Quelle application
voyez-vous à ce montage ?
9)c) Est-il important que le fil soit placé sur
l’axe du tore ?
| Réponse
9a | Réponse
9b | Réponse
9c |