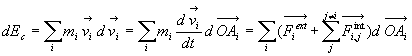Notions simples de Mécanique du solide
1. Définition d’un solide. Degrés
de liberté
Un solide est un corps dont les différents points restent à
des distances constantes les uns des autres au cours du mouvement.
Un solide pouvant se mouvoir librement a sa position déterminée
par la donnée de six paramètres : la position d’un point
(trois coordonnées) et trois angles qui, dans le cas général,
sont les angles d’Euler et, plus souvent, des angles adaptés au
solide (par exemple pour un bateau, des angles correspondant au changement
de cap, au tangage et au roulis).
On dit que, dans le cas le plus général de mouvement,
le solide possède six degrés de liberté.
Des liaisons peuvent réduire les mouvements possibles et, en
conséquence, diminuer le nombre de degrés de liberté
; ainsi un solide en rotation autour d’un axe fixe a un degré de
liberté.
2. Distribution des vitesses dans un
solide
2.1. Mouvements particuliers
Translation : à chaque instant, tous les points d’un solide
ont même vitesse.
 quelques soient
A et B appartenant au solide.
quelques soient
A et B appartenant au solide.
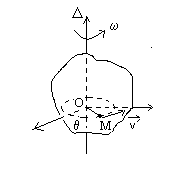 |
Rotation autour d’un axe fixe D
: L’intensité de la vitesse du point M appartenant au solide, situé
à la distance 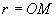 de
l’axe de rotation, est égal à de
l’axe de rotation, est égal à 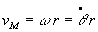 .
Sa direction est dans le plan perpendiculaire à l’axe de rotation,
tangentiellement au cercle de rayon OM. .
Sa direction est dans le plan perpendiculaire à l’axe de rotation,
tangentiellement au cercle de rayon OM.
En introduisant un vecteur rotation  où
où  est le vecteur unitaire de l’axe de rotation, on peut écrire :
est le vecteur unitaire de l’axe de rotation, on peut écrire :
 |
Dans cette dernière relation, on remarquera que le point O
est quelconque sur l’axe de rotation.
2.2. Mouvement général d’un solide
Soient deux points A et B quelconques d’un solide.
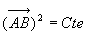 ð
ð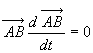 ð
ð ð
ð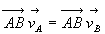
Cette dernière relation est caractéristique d’un torseur
( ensemble d’un champ de moments et d’un vecteur résultant) et le champ
de vitesse est donné par la relation :
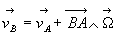
Remarques sur la distribution des vitesses dans un solide
- à chaque instant la vitesse
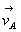 d’un point quelconque et le vecteur rotation
d’un point quelconque et le vecteur rotation 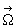 ,
soient six composantes, définissent parfaitement le champ de vitesses
dans le solide
,
soient six composantes, définissent parfaitement le champ de vitesses
dans le solide
- soient deux points I et J de l’axe instantané de rotation
à un instant donné, c’est à dire de l’axe support de
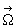 ,
l’écriture du champ de vitesse pour ces deux points donne
,
l’écriture du champ de vitesse pour ces deux points donne 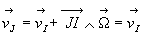
Les points de l’axe instantané de rotation sont en translation.
Le mouvement général, à un instant donné,
d’un solide est la superposition d’une translation suivant l’axe instantané
de rotation et d’une rotation autour de cet axe.
Le champ de vitesses dans un solide est un champ de moments dont le vecteur
résultant est le vecteur rotation 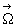 .
A chaque instant, le mouvement dans un solide se décompose en un mouvement
de translation de direction le vecteur rotation et en une rotation autour de cette
direction.
.
A chaque instant, le mouvement dans un solide se décompose en un mouvement
de translation de direction le vecteur rotation et en une rotation autour de cette
direction.
3. Composition des mouvements
En Mécanique du solide, la composition des mouvements prend une
importance particulière, le référentiel relatif a
pour origine un point particulier G que nous définirons comme
étant le centre de masse et les axes Gxyz respecteront
les éventuelles symétries du solide.
Un point A’, coïncidant au temps t avec le point A, fixe dans le
référentiel  a un mouvement, appelé mouvement d’entraînement, dans le
référentiel
a un mouvement, appelé mouvement d’entraînement, dans le
référentiel 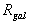
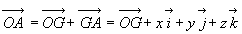 ð
ð
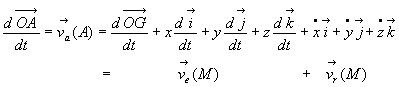
La vitesse absolue (dans le référentiel 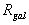 )
est la somme de la vitesse d’entraînement et de la vitesse relative (dans
le référentiel
)
est la somme de la vitesse d’entraînement et de la vitesse relative (dans
le référentiel  )
)
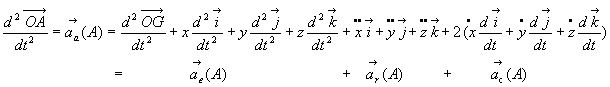
L’accélération absolue est la somme de l’accélération
d’entraînement, de l’accélération relative et d’un
terme appelé accélération de Coriolis, résultat
d’un couplage entre le mouvement d’entraînement et le mouvement relatif.
Interprétation du terme de Coriolis en termes de champ de
vitesses dans un solide
Si nous remarquons que dans le référentiel  ,
les points O, I, J, K sont à distances constantes et peuvent être
considérés comme des points d’un même solide, alors on peut
écrire :
,
les points O, I, J, K sont à distances constantes et peuvent être
considérés comme des points d’un même solide, alors on peut
écrire :
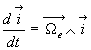 ;
;  ;
; 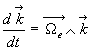 et
et 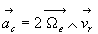 où
où  représente le vecteur rotation du mouvement d’entraînement (c’est
à dire de
représente le vecteur rotation du mouvement d’entraînement (c’est
à dire de  par rapport à
par rapport à  )
)
Opérations de dérivation
Soit un vecteur quelconque 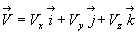
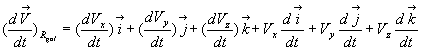
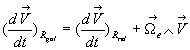 Le référentiel
de dérivation doit être précisé. Par défaut,
il s ‘agit du référentiel
Le référentiel
de dérivation doit être précisé. Par défaut,
il s ‘agit du référentiel 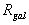 .
.
Composition des vitesses angulaires
Soient deux points quelconques A et B du solide pour lesquels
nous écrivons les vitesses absolues, d’entraînement et relatives.
 ;
; 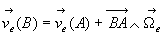 ;
; 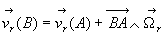

ð cette relation nous montre que l’on peut décomposer un mouvement de rotation
en rotations autour d’axes connus.
cette relation nous montre que l’on peut décomposer un mouvement de rotation
en rotations autour d’axes connus.
Les angles d’Euler
Ils permettent la " transformation " du référentiel OXYZ
en référentiel Oxyz, parallèle à Gxyz.
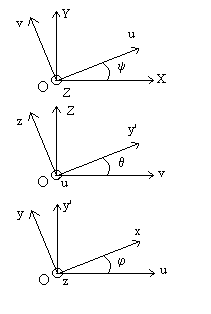 |
Les angles 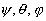 sont les trois angles d’Euler. Ils portent des noms liés à
leur application en Astronomie :
sont les trois angles d’Euler. Ils portent des noms liés à
leur application en Astronomie : 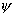 est l’angle de précession,
est l’angle de précession,  l’angle de nutation et
l’angle de nutation et 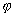 l’angle de rotation propre.
l’angle de rotation propre.
On a souvent besoin d’écrire le vecteur rotation 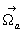 dans la base du référentiel
dans la base du référentiel  [
[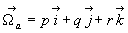 ]. ].
Compte tenu des angles d’Euler, ce vecteur peut être écrit 
Par projection, on montre que :
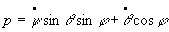 ; ; 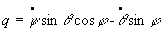 ;
;
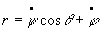 |
4. Eléments cinétiques
d’un solide
Un solide peut être constitué par une distribution discrète
de masses ponctuelles ou par une distribution continue de masses. Dans ce dernier
cas, on définit la masse volumique 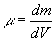 où dm est la masse contenue dans le volume élémentaire
dV.
où dm est la masse contenue dans le volume élémentaire
dV.
4.1. Masse. Centre de masse
La masse du solide est définie par  ,
le centre de masse (ou centre d'inerrtie) par
,
le centre de masse (ou centre d'inerrtie) par 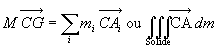 (C point quelconque)
(C point quelconque)
4.2. Torseur cinétique
Résultante cinétique : 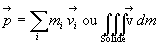
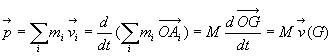
La résultante cinétique (ou quantité de mouvement
total) est égale à la quantité de mouvement qu’aurait
le centre de masse affecté de toute la masse.
Moment cinétique : 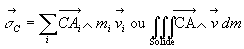
Il découle, par application directe des définitions, que 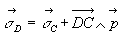 relation appelée relation de transfert du torseur entre les points
C et D.
relation appelée relation de transfert du torseur entre les points
C et D.
Moment cinétique par rapport à un axe D
Soit 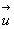 le vecteur
unitaire de l’axe D et E un point de
cet axe.
le vecteur
unitaire de l’axe D et E un point de
cet axe.
Par définition, le moment cinétique par rapport l’axe D
est égal à 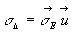 .
.
On montre, par application directe des définitions, que ce résultat
est indépendant du point E appartenant à D.
Ainsi, si F est un autre point de D,
: 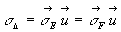
4.3. Torseur dynamique
Résultante dynamique : 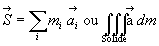
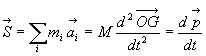
Moment dynamique : 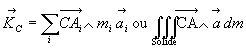
Il découle, par application directe des définitions, que  relationde transfert du torseur entre les points C et D.
relationde transfert du torseur entre les points C et D.
4.4. Torseur dynamique et torseur cinétique
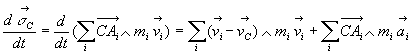

Il existe des cas où la dérivée du moment cinétique
est égale au moment dynamique :
- C fixe (généralement 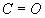 )
)
- 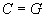 ou
ou 
4.5. Energie cinétique
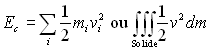
4.6. Théorèmes de Koenig
4.6.1 Référentiel barycentrique
On appelle référentiel barycentrique 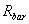 un référentiel d’origine le centre de masse G en translation
par rapport au référentiel
un référentiel d’origine le centre de masse G en translation
par rapport au référentiel 
Par suite, 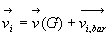 où
où  .
De même,
.
De même, 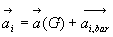
Par définition du centre de masse 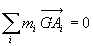 ð
ð
La résultante cinétique est nulle dans le référentiel
barycentrique.
4.6.2. Premier théorème de Koenig
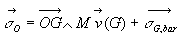 où
où 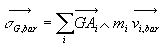 (démonstration : application directe des définitions)
(démonstration : application directe des définitions)
Le moment cinétique d’un solide est égal à la somme
du moment cinétique du centre de masse affecté de toute la
masse du solide et du moment cinétique du solide par rapport au
centre de masse évalué dans le référentiel
barycentrique.
4.6.3. Deuxième théorème de Koenig
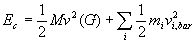 (démonstration
: application directe des définitions)
(démonstration
: application directe des définitions)
L’énergie cinétique d’un solide est égale à
la somme de l’énergie cinétique du centre de masse affecté
de toute la masse du solide et de l’énergie cinétique du
solide correspondant à son mouvement dans le référentiel
barycentrique.
4.7. Cas particulier du solide en mouvement autour d’un axe fixe
D
4.7.1. Moment cinétique par rapport à l’axe
D
Soit 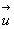 le vecteur
unitaire de l’axe D, O un point de
l’axe et A un point quelconque du solide.
le vecteur
unitaire de l’axe D, O un point de
l’axe et A un point quelconque du solide.
 où
où 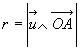 est la distance de A à l’axe D.
est la distance de A à l’axe D.
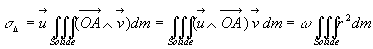
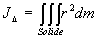 est appelé
le moment d’inertie du solide par rapport à l’axe D.
est appelé
le moment d’inertie du solide par rapport à l’axe D.
| 4.7.2. Théorème
d’Huygens
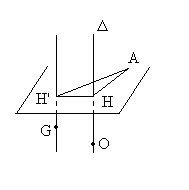
|
Par le centre de masse G, on trace un
axe parallèle à D.
H et H’ sont les intersections des deux axes avec un
plan perpendiculaire à ces axes passant par A.
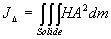
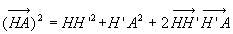
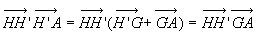
|
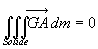 ð
ð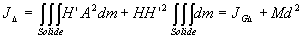 où
où  est
le moment d’inertie par rapport à l’axe parallèle à D
passant par G et
est
le moment d’inertie par rapport à l’axe parallèle à D
passant par G et 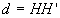 la distance entre les deux axes.
la distance entre les deux axes.
Ce résultat constitue le théorème d’Huygens, souvent
utilisé pour calculer des moments d’inertie.
Le calcul des moments d’inertie pour des barres, des cylindres ou
des sphères est à connaître. Le lecteur doit savoir
démontrer que les moments d’inertie :
- d’une tige homogène de longueur l, de masse m, de section négligeable,
par rapport à un axe perpendiculaire à la direction de la tige
passant par son centre de masse 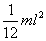
- d’un cylindre plein homogène, de rayon R, de masse m, par rapport
à son axe de révolution 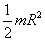
- d’une sphère pleine homogène, de rayon R, de masse m, par
rapport à un diamètre 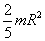
4.7.3. Moment dynamique par rapport à l’axe D
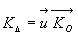 et
et 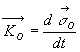
Par suite, 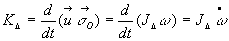
4.7.4. Energie cinétique

4.8. Solide en rotation autour d’un point fixe O (ou mouvement du
solide dans le référentiel barycentrique, G = O). Opérateur
d’inertie.
4.8.1. Moment cinétique par rapport en O
Soit A un point quelconque du solide. 
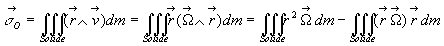
Si dans la base cartésienne habituelle, on écrit :
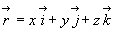 ;
;  ;
; 
on obtient 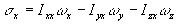 ,
, 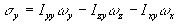 et
et 
avec 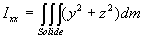 ;
; 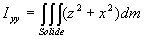 ;
; 
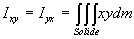 ;
;  ;
; 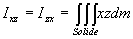
Ces relations peuvent être écrites sous forme matricielle.
 soit aussi
soit aussi 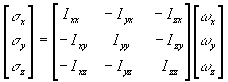
4.8.2. Tenseur d’inertie
La matrice 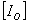 fait correspondre à tout vecteur
fait correspondre à tout vecteur 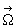 un vecteur
un vecteur 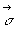 et ceci indépendamment du repère choisi. Cette matrice possède
un caractère géométrique intrinsèque qui implique
des propriétés bien particulières de transformation des
ses coefficients (symétriques par rapport à la diagonale) vis
à vis d’un changement de repère.
et ceci indépendamment du repère choisi. Cette matrice possède
un caractère géométrique intrinsèque qui implique
des propriétés bien particulières de transformation des
ses coefficients (symétriques par rapport à la diagonale) vis
à vis d’un changement de repère.
C’est pourquoi, on donne à 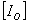 le nom de tenseur d’inertie. Il est appelé tenseur central d’inertie
si le point O coïncide avec le centre de masse G.
le nom de tenseur d’inertie. Il est appelé tenseur central d’inertie
si le point O coïncide avec le centre de masse G.
| Nous pouvons appliquer les propriétés
du calcul matriciel, en particulier la diagonalisation dans les directions
propres de la matrice appelées, par définition, axes principaux
du solide. |
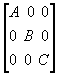 |
Le tenseur est alors appelé tenseur principal d’inertie et tenseur
central principal d’inertie si le point O coïncide avec le centre
de masse G.
Dans un certain nombre de problèmes simples, les axes principaux
sont facilement repérables par l’étude des symétries
du solide.
Exemples
4.8.3. Energie cinétique
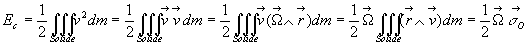
Sous forme matricielle, ce résultat peut être écrit :  où la matrice uniligne
où la matrice uniligne  est la matrice transposée de la matrice unicolonne
est la matrice transposée de la matrice unicolonne  .
.
4.8.4. Moment dynamique. Energie cinétique
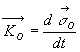 si O est fixe ou
se confond avec le centre de masse G.
si O est fixe ou
se confond avec le centre de masse G.
Soit 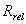 un référentiel
d’origine O lié au solide et dont les axes coïncident avec les axes
principaux. On appelle
un référentiel
d’origine O lié au solide et dont les axes coïncident avec les axes
principaux. On appelle  les vecteurs unitaires de ces axes.
les vecteurs unitaires de ces axes.
La vitesse angulaire du référentiel 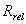 dans le référentiel absolu
dans le référentiel absolu 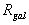 se confond avec la vitesse angulaire du mouvement d’entraînement ð
se confond avec la vitesse angulaire du mouvement d’entraînement ð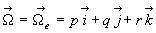
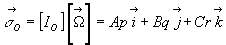
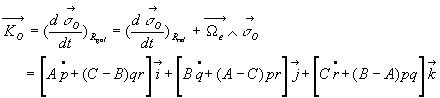
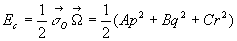
4.8.5. Calcul du moment d’inertie par rapport à un axe quelconque.
Calcul des produits d’inertie.
-
Nous imaginons un solide en rotation autour d’un axe D
de vecteur unitaire
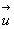 . O
est un point de cet axe.
. O
est un point de cet axe.
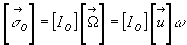 ð
ð ð
ð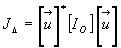
-
Lorsque le tenseur d’inertie n’est pas rapporté aux axes principaux,
ses composantes comportent les produits d’inertie. Pour déterminer
ces termes, le plus simple est de déterminer le tenseur principal
d’inertie puis de faire un changement de repère.
Soit 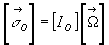 défini
dans des axes principaux et
défini
dans des axes principaux et 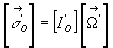 défini dans un repère quelconque.
défini dans un repère quelconque.
Soit 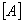 la matrice
rotation associée au changement de repère ð
la matrice
rotation associée au changement de repère ð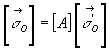 et
et 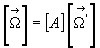
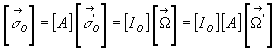
 ð
ð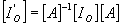
5. Forces s’exerçant sur un
solide
Outre les forces de champ (pesanteur, gravitation, électrostatique),
interviendront les forces dues aux liaisons qui limitent les possibilités
de mouvement du solide. Ces forces constituent l’ensemble des forces
extérieures qui s’exercent sur le solide.
A ces forces, il convient d’ajouter les forces intérieures
qui assurent la cohésion du solide.
5.1. Champ de pesanteur uniforme 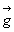
Le poids sera défini par 
Moment des forces de pesanteur
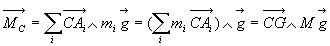
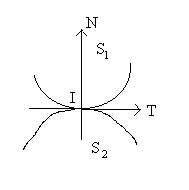
5.2. Liaison par contact direct entre deux solides
de pivotement (rotation autour de l’axe normal N de vecteur unitaire 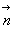 ).
).
On appelle vitesse de glissement, le vecteur 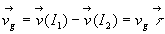 .
.
En absence de glissement, 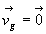 .
Le roulement sans glissement est un cas courant très important
où cette condition s’applique.
.
Le roulement sans glissement est un cas courant très important
où cette condition s’applique.
Lois du frottement de Coulomb
A cause de l’impénétrabilité des solides, le solide 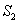 exerce sur le solide
exerce sur le solide 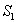 une force
une force 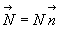 (évidemment la réciproque est vraie, les deux forces obéissant
au principe de l'action et de la réaction).
(évidemment la réciproque est vraie, les deux forces obéissant
au principe de l'action et de la réaction).
Les aspérités (rugosité des états de surface des
solides) empêchent les mouvements relatifs.
D’une manière générale, les effets des forces qui s’opposent
au roulement ou au pivotement sont faibles devant les effets des forces qui
s’opposent au glissement et nous n’étudierons que ces dernières.
Le solide 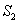 exerce
sur le solide
exerce
sur le solide 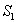 une force
une force 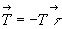 qui s’oppose au glissement.
qui s’oppose au glissement.
Si 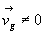 , alors
, alors 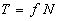 où f est le coefficient de frottement qui dépend
en particulier de l’état des surfaces en contact.
où f est le coefficient de frottement qui dépend
en particulier de l’état des surfaces en contact.
Si 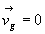 , alors
, alors 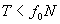
Généralement on prend 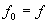 même si, dans la réalité
même si, dans la réalité 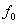 est supérieur à f.
est supérieur à f.
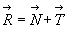 est l’ensemble
des réactions en I sur
est l’ensemble
des réactions en I sur 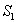 .
Bien sur,
.
Bien sur, 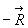 sera l’ensemble des réactions en I sur
sera l’ensemble des réactions en I sur 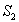 .
.
Travail des forces de frottement
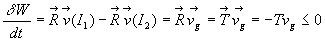
Le travail des forces de frottement est négatif ou nul. Il se
traduit par des pertes d’énergie mécanique.
Le cas du roulement sans glissement correspond à un travail des forces
de frottement nul.
6. Dynamique du solide
Les forces extérieures sur un élément i sont notés 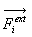 ,
celles intérieures
,
celles intérieures 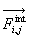 (l’indice j signifie que cette force est due à un élément
interne j).
(l’indice j signifie que cette force est due à un élément
interne j).
On se place dans un référentiel galiléen d’origine
O noté  .
.
Remarque : pour une meilleure clarté de la présentation
sur les forces intérieures, nous utilisons la notation 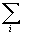 plutôt
que la notation
plutôt
que la notation  .
.
6.1. Théorèmes généraux de la dynamique du solide
(ou principe de la dynamique du solide)
Résultante dynamique
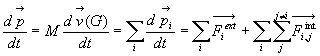
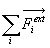 est la résultante
des forces extérieures, nous la noterons
est la résultante
des forces extérieures, nous la noterons 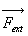
Moment dynamique

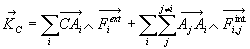 en faisant attention
de ne compter qu’une seule fois les termes de la double sommation.
en faisant attention
de ne compter qu’une seule fois les termes de la double sommation.
Il y a deux points de vue :
- soit nous admettons le Principe de l’action et de la réaction
[
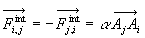 ] et concluons
au théorème de la résultante dynamique
] et concluons
au théorème de la résultante dynamique  et au théorème du moment dynamique
et au théorème du moment dynamique 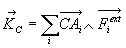
-
soit nous admettons les relations précédentes que nous appelons
Principe
de la dynamique des solides (dans un référentiel galiléen,
le torseur dynamique en un point quelconque est égal à au
torseur des forces extérieures en ce point) et concluons au théorème
de l’action et de la réaction pour les forces intérieures
d’un solide.
Remarques :
- On montre, sans difficulté, que les forces extérieures forment
un torseur puisqu’elles obéissent à la relation de transfert
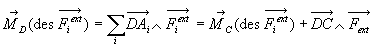
- On notera que le mouvement du centre de masse est identique au mouvement
d’un objet ponctuel de masse égale à la masse totale du solide.
- De nombreux ouvrages utilisent systématiquement la dérivation
du moment cinétique pour calculer le moment dynamique.
Nous avons vu en 4.4. que 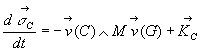
Cette relation appliquée en  ou
ou 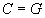 est facile
d’emploi puisque
est facile
d’emploi puisque
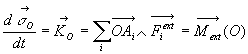 ou
ou 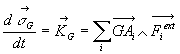
[en notant que 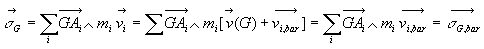 ð
ð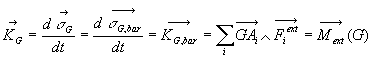 ]
]
En un point mobile C, nous préférons, à l’utilisation
de la formule du paragraphe 4.4, le calcul du moment dynamique par la relation
de transfert à partir du moment dynamique en G, à savoir
: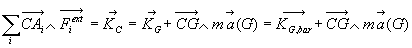
- L’application de la résultante dynamique ou du moment dynamique
peut être faite dans un référentiel non galiléen
à condition d'introduire les forces d’inertie. ne nous paraît
pas présentée d’intérêt réel
6.2. Le théorème de l’énergie cinétique
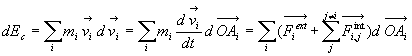
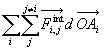 fait
apparaître des termes
fait
apparaître des termes 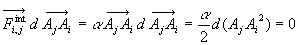 puisque la distance de deux points quelconques d’un solide est constante.
puisque la distance de deux points quelconques d’un solide est constante.
Ainsi, 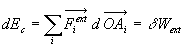 où
où 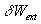 est
le travail élémentaire des forces extérieures.
est
le travail élémentaire des forces extérieures.
Soit, après intégration,  (travail des forces extérieures)
(travail des forces extérieures)
Ce résultat constitue le " théorème "
de l’énergie cinétique pour un solide.
6.3. Remarque sur la conservation de l’énergie mécanique
Comme nous l’avons fait en dynamique du point, on peut séparer
les forces extérieures en forces conservatives qui dérivent d’une
énergie potentielle et en forces non conservatives.
On obtient 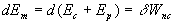 .
.
Les forces non conservatives sont les forces d’opérateur extérieur
ou les forces de frottement.
Le travail des forces de frottement est nul :
- en l’absence de forces de frottement
- dans le cas d’un roulement sans glissement (paragraphe 5.2)
C’est un résultat important, car en l’absence de
forces d’opérateur extérieur, l’énergie mécanique
se conserve. Son écriture fournit directement une intégrale
première du mouvement et permet, généralement de se passer
du théorème du moment dynamique
6.4. Ecriture générale du travail des forces extérieures
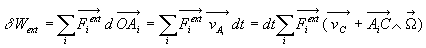

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

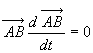 ð
ð ð
ð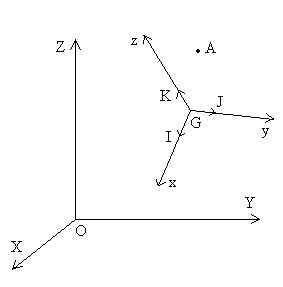
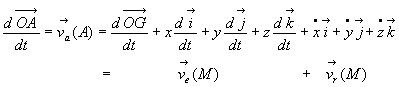
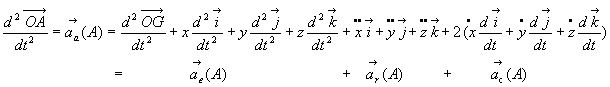
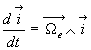 ;
;  ;
; 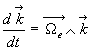 et
et 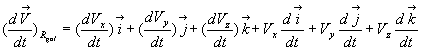
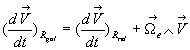 Le référentiel
de dérivation doit être précisé. Par défaut,
il s ‘agit du référentiel
Le référentiel
de dérivation doit être précisé. Par défaut,
il s ‘agit du référentiel 
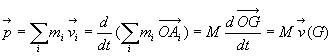
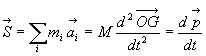
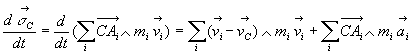

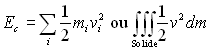
 .
De même,
.
De même, 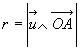 est la distance de A à l’axe D.
est la distance de A à l’axe D.
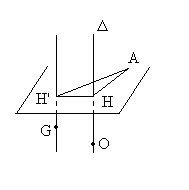
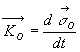
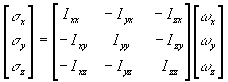

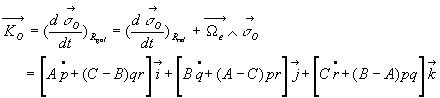
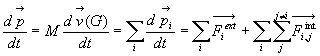
 et au théorème du moment dynamique
et au théorème du moment dynamique 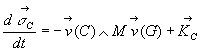
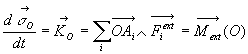 ou
ou 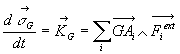
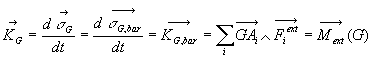 ]
]