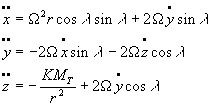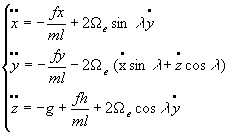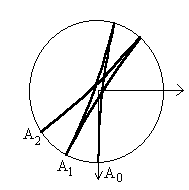Quelques phénomènes de dynamique terrestre
Dans un référentiel lié au sol terrestre, l'équation
fondamentale de la dynamique s'écrit :
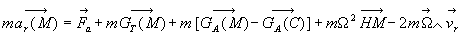
1. Le champ de pesanteur terrestre
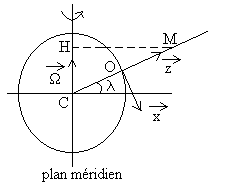 |
Le poids d'un corps 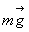 et le champ de pesanteur
et le champ de pesanteur 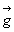 sont définis par la relation :
sont définis par la relation :
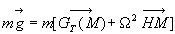
où 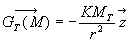 est le champ d’attraction universelle à un distance
est le champ d’attraction universelle à un distance 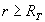 rayon de la terre
rayon de la terre

On appelle verticale la direction du vecteur 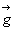 . . |
Sur le sol terrestre (ou au voisinage), 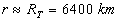 ð
ð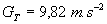 et
et 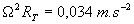 , aussi
en première approximation on confond assez souvent
, aussi
en première approximation on confond assez souvent 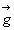 et
et  .
.
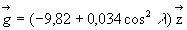 explique bien
les variations du champ de pesanteur terrestre. Souvent, on se contente de
explique bien
les variations du champ de pesanteur terrestre. Souvent, on se contente de  .
.
2. La déviation vers l'Est
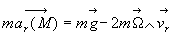 si on néglige
l'attraction universelle des astres autres que la Terre et s'il n'y a pas de
forces appliquées sur l'objet.
si on néglige
l'attraction universelle des astres autres que la Terre et s'il n'y a pas de
forces appliquées sur l'objet.
En projetant sur le repère Oxyz, on obtient :
A l'instant 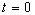 ,
on lâche l'objet, sans vitesse initiale, d'une hauteur par rapport au
sol
,
on lâche l'objet, sans vitesse initiale, d'une hauteur par rapport au
sol  .
.
Par intégration, en négligeant z devant  et
et 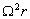 devant
devant 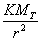 ,
on trouve
,
on trouve 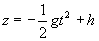 et
et  .
.
Ce phénomène est connu sous le nom de déviation
à l'est.
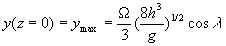 est égal
à 27 mm pour
est égal
à 27 mm pour  et
et 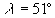 . L'effet
est donc très faible et souvent négligé.
. L'effet
est donc très faible et souvent négligé.
Il existe, dans l'hémisphère Nord (Sud), une déviation
au Sud (Nord) encore plus négligeable.
3. Le pendule de Foucault 
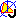
 |
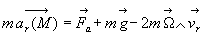
Le pendule simple de longueur 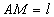 reste peu incliné par rapport à l'axe vertical.
reste peu incliné par rapport à l'axe vertical.
ð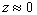 ;
;  ; ; 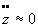
ð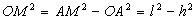 (
(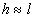 ) )
ð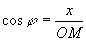 ;
; 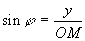
ð ;
; 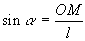 |
Le fil du pendule simple est inextensible et la masse m est soumise
à son poids et à la tension 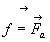 due au fil.
due au fil.
Le vecteur rotation propre de la Terre est égale à : 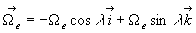 ,
,
si bien que 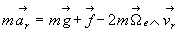 ð
ð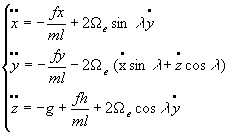
Dans la dernière équation, le terme  est négligeable (il n’est pas écrit lorsque qu’on néglige
la force de Coriolis), le terme
est négligeable (il n’est pas écrit lorsque qu’on néglige
la force de Coriolis), le terme 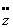 aussi (pendule en permanence peu écarté de la verticale). Ceci
permet d’écrire
aussi (pendule en permanence peu écarté de la verticale). Ceci
permet d’écrire 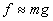 .
.
Les équations deviennent 
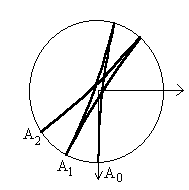 |
Pour résoudre ce système, on peut le découpler par
dérivation ou, mieux, utiliser la variable complexe  qui conduit à
qui conduit à 
En intégrant, on obtient :
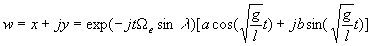 |
Cette solution fait apparaître un mouvement tournant dans le plan Oxy
à la pulsation 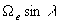 (période
(période 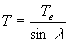 où
où 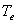 est
la période sidérale de la Terre). La rotation s'effectue dans
le sens inverse dans l'hémisphère Nord et dans le sens direct
dans l'hémisphère Sud.
est
la période sidérale de la Terre). La rotation s'effectue dans
le sens inverse dans l'hémisphère Nord et dans le sens direct
dans l'hémisphère Sud.
Ce phénomène a été étudié
par Foucault au siècle dernier à l'aide d'un pendule de 67
m
de longueur suspendu au dôme du Panthéon.
Remarque : Il existe d'autres phénomènes mettant
en évidence la rotation de la Terre sur elle-même, les plus
connus sont le mouvement tourbillonnaire de vidange d'un lavabo,
l'érosion préférentielle d'une des rives d'un fleuve
s'écoulant
vers le Nord ou vers le Sud.
4. Le phénomène des marées 
Si l'on considère la masse d'eau considérable d'un océan,
il n'est plus possible de négliger le terme 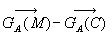 qui est responsable des marées.
qui est responsable des marées.
Pour commencer, nous ne considérons que l'influence de la Lune.
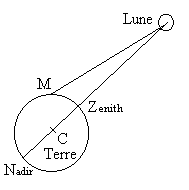 |
Aux deux points Z et N, 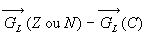 est orienté vers l'extérieur de la Terre et s'oppose à
l'attraction terrestre tout en restant de même direction.
est orienté vers l'extérieur de la Terre et s'oppose à
l'attraction terrestre tout en restant de même direction.
En un point M quelconque,  a une composant horizontale [maximale si Z(ou N)CM vaut 45°] produisant
une déviation de la verticale.
a une composant horizontale [maximale si Z(ou N)CM vaut 45°] produisant
une déviation de la verticale.
Il en est de même pour le Soleil.
Les déviations maximales sont de 0,017" pour l'action de la
Lune, de 0,008" pour celle du Soleil. |
Ces déviations, bien que très faibles, sont mises en évidence
par la variation de la surface des océans : celle-ci se modifie
à chaque instant de manière à être constamment
perpendiculaire à la verticale.
Les effets dus aux autres astres sont négligeables, de sorte
qu'en pratique seuls les effets dus à la Lune et au Soleil sont
à considérer . Ces effets s'ajoutent lorsque le Soleil, la
Terre et la Lune sont alignés : ce sont les marées de
vive-eau, ils se compensent lorsque les directions Soleil-Terre et
Terre-Lune sont perpendiculaires : ce sont les marées de morte-eau.
Enfin, aux équinoxes de printemps et d'automne, l'effet dû
au Soleil est maximal : ce sont les marées d'équinoxe.
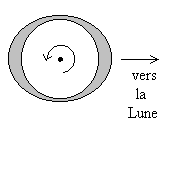 |
La rotation de la Terre sur elle-même
explique l'existence de deux marées hautes et de deux marées
basses chaque jour. |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()