Table des matières
Joindre l'auteur

CHAPITRE 5 : Les régimes variables. Le théorème de superposition de Duhamel

Plan

1. La source de chaleur change d’intensité au temps t = t’
2. Le Théorème de superposition de Duhamel
3. Exemples

Dans les régimes variables, les sources évoluent dans le temps si bien que le champ de température dépend de l’espace et du temps.

Le champ de températures est régi par le système d’équations :

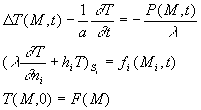
Par superposition, la solution peut être recherchée sous la forme :

Le premier terme du champ de température est du type de ceux que nous avons étudiés dans les chapitres 2, 3 et 4 puisque les sources ont constamment leur valeur au temps t = 0.
Le deuxième terme du champ de température (où on remarquera que la température initiale a été rendue, par superposition, identiquement nulle) est d’un type différent puisqu’il fait intervenir les variations des sources dans le temps, c’est à dire et .

La solution est recherchée sous la forme :
où, dans chacun des systèmes, toutes les sources sont nulles sauf une.

1. La source de chaleur change d’intensité au temps t = t’
 
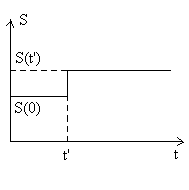Au temps t = t’, la source de chaleur passe brusquement de la valeur S(0) à la valeur S(t’).
Le champ de température est donné par :
où


Le deuxième terme du champ de température est identiquement nul pour  et évolue, sous l’influence de la seule source constante , à partir de  .

Pour traiter ce deuxième terme, il suffit de placer l’origine des temps en  si bien que la solution peut être écrite :

La linéarité des équations de Conduction de la Chaleur permet d’écrire cette dernière solution sous la forme :
qui fait explicitement apparaître un champ de température proportionnel à la variation d’intensité de la source. On se rappellera que le deuxième terme du champ de température est nulle si .

2. Le Théorème de superposition de Duhamel
 
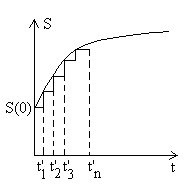L’intensité de la source évolue continument, au moins par partie.
En appliquant le résultat du paragraphe 1, le champ de température s’écrira :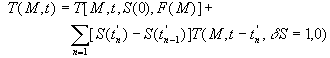

avec .
Pour une source continue, nous passons à la limite en faisant .

Alors  et nous obtenons la première formulation du théorème de Duhamel :
 

Une intégration par parties conduit à :

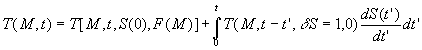
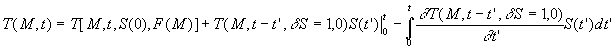
En remarquant que : , ,

, on obtient :

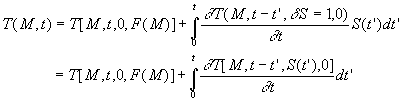
Or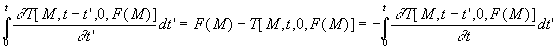 

En reportant 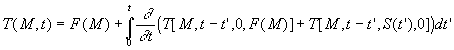, on obtient la deuxième formulation du théorème de Duhamel :

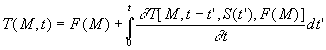
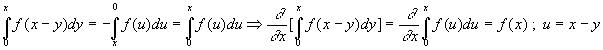
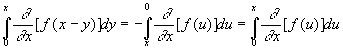
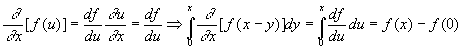
Donc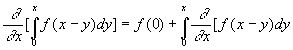 

En appliquant ce résultat sur la deuxième formulation, on obtient la troisième formulation :

3. Exemples

Le milieu semi-infini est, maintenant, soumis à un échelon de flux de chaleur c’est à dire à une densité de flux de chaleur pendant une durée (voir dessin ci-après).
La solution consiste à superposer, au flux de chaleur commençant au temps , un flux de chaleur opposé commençant au temps .

Un mur fini isolé sur sa face x = L, initialement à température uniforme de référence, est soumis à une densité de flux de chaleur.

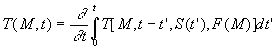
Nous envisagerons deux cas :

- l’échelon de flux où la solution est immédiate,

- la montée linéaire jusqu’à la valeur limite

Nous utilisons la première formulation.

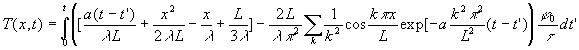
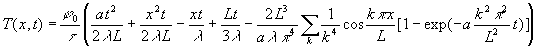
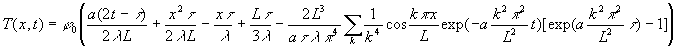que l’on obtient en continuant la source  et en créant une source .

Le lecteur pourra reprendre ces exemples avec les deuxième et troisième formulations. Il remarquera que ces formulations restent efficaces même lorsque les fonctions sources présentent des discontinuités. Cependant nous conseillons d’utiliser au maximum les possibilités de superposition des solutions.